面内平面要素におけるばね剛性行列の成分に関する被積分項を以下に示す.ただし,回転は時計回りを正とする.
\[
\left\{
\begin{array}{l}
k_{11} = l_1^2 k_n + l_2^2 k_s \\
k_{12} = l_1 m_1 k_n + l_2 m_2 k_s \\
k_{13} =-l_1 \{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\} k_n
-l_2 \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\} k_s \\
k_{14} = -k_{11} \\
k_{15} = -k_{12} \\
k_{16} = l_1 \{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\} k_n
+l_2 \{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\} k_s
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
k_{22} = m_1^2 k_n + m_2^2 k_s \\
k_{23} =-m_1 \{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\} k_n
-m_2 \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\} k_s \\
k_{24} =-l_1 m_1 k_n - l_2 m_2 k_s \\
k_{25} = -k_{22} \\
k_{26} = m_1 \{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\} k_n
+m_2 \{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\} k_s
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
k_{33} = \{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\}^2 k_n
+ \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\}^2 k_s \\
k_{34} = l_1 \{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\} k_n
+ l_2 \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\} k_s \\
k_{35} = m_1 \{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\} k_n
+m_2 \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\} k_s \\
K_{36} =-\{l_1 (y-y_{_{G_1}}) - m_1 (x-x_{_{G_1}})\}
\{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\} k_n \\
\hspace{3em}
- \{l_2 (y-y_{_{G_1}}) - m_2 (x-x_{_{G_1}})\}
\{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\} k_s
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
k_{44} = l_1^2 k_n + l_2^2 k_s \\
k_{45} = l_1 m_1 k_n + l_2 m_2 k_s \\
k_{46} =-l_1 \{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\} k_n
-l_2 \{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\} k_s
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
k_{55} = m_1^2 k_n + m_2^2 k_s \\
k_{26} =- m_1 \{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\} k_n
-m_2 \{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\} k_s
\end{array}
\right.
\]
\[
k_{66} = \{l_1 (y-y_{_{G_2}}) - m_1 (x-x_{_{G_2}})\}^2 k_n
+ \{l_2 (y-y_{_{G_2}}) - m_2 (x-x_{_{G_2}})\}^2 k_s \\
\]
前節で示した被積分項は座標値の関数となっている.数値積分を行わずに陽な形式で剛性行列を利用するためには予め積分を行つておく必要がある.次に,この積分について説明する.
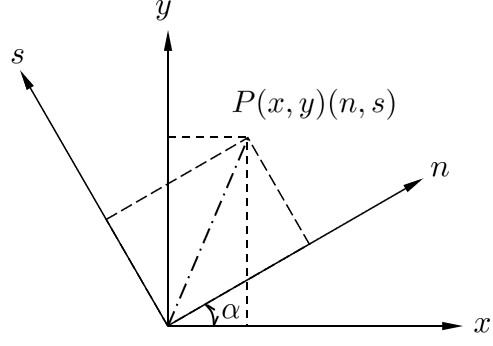
$\hspace{1em}$図7.1 全体座標系と局所座標系
図7.1 は直角座標系 $x-o-y$ を $\alpha$ なる角度だけ回転して得られる新たな直角座標系 $n-o-s$ を表している.いま,任意の点 $P$ の $x-o-y$ 座標系に関する座標値を $(x,y)$,$n-o-s$ 座標系に関する座標値を $(n,s)$ とすれば,これらの間に以下のような幾何学的な関係が成立する.
\[
\left\{
\matrix{
n = \hspace{1em} l \cdot x + m \cdot y \cr
s = -m \cdot x + l \cdot y
}
\right.
\;\;\;\;
\left\{
\matrix{
x = l \cdot n - m \cdot s \cr
y = m \cdot n + l \cdot s
}
\right.
\]
\[
(l,m)
=
(\cos \alpha, \sin \alpha)
\]
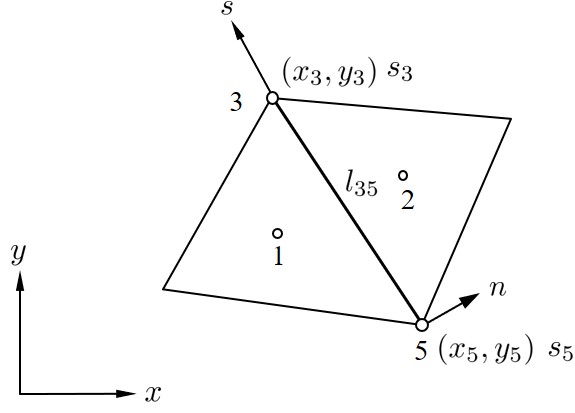
次に,上記の関係を用いて三角形要素の各辺に沿つた線積分を行うことにする.まず,積分を実行する前に使用する記号を
図7.2 に示す.
$\hspace{6em}$図7.2 記号の定義
\[
l_{35}(辺35の長さ)= \sqrt{ (x_3-x_5)^2 + (y_3-y_5)^2}
\]
\[
l(方向余弦)= (y_3 - y_5)/l_{35}
\]
\[
m(方向余弦)= -(x_3 - x_5)/l_{35}
\]
\[
s_3 = (x_3,y_3) \;\;\;\; s_5 = (x_5,y_5)
\]
このとき,以下の関係が得られる.
\[
\int_{s_5}^{s_3} ds
= \left[s\right]_{s_5}^{s_3}
= (s_3 - s_5)
\]
\[\hspace{4em}
= (-mx_3 + l y_3) - (-m x_5+ly_5)
= l_{35}
\]
\[
\int_{s_5}^{s_3} x ds
= \int_{s_5}^{s_3} (ln-ms) ds
= \left[ lns - \frac{1}{2}ms^2 \right]_{s_5}^{s_3} (s_3 - s_5)
\]
\[\hspace{4em}
= - \frac{l_{35}}{2} m (s_3 + s_5)
= \frac{l_{35}}{2} (x_3 + x_5)
\]
\[
\int_{s_5}^{s_3} x^2 ds
= \int_{s_5}^{s_3} (ln-ms)^2 ds
\]
\[\hspace{4em}
= \frac{l_{35}}{2} \left\{ (ln_3 - ms_3)^2
+ (ln_3 -ms_3)(ln_5-ms_5)
+ (ln_5-ms_5)^2
\right\}
\]
\[\hspace{4em}
= \frac{l_{35}}{3} ( x_3^2 + x_3 x_5 + x_5^2 )
\]
\[
\int_{s_5}^{s_3} xy ds
= \int_{s_5}^{s_3} (ln-ms)(mn+ls) ds
= \left[ \frac{1}{3} lms^3 \right]_{s_5}^{s_3}
\]
\[\hspace{4em}
= \frac{l_{35}}{6}( 2 x_3 y_3 + x_3 y_5 + x_5 y_3 + 2 x_5 y_5 )
\]
以上の結果より以下の積分公式が得られる.
\[
\int_{s_5}^{s_3} ds
=
l_{35}
\]
\[
\int_{s_5}^{s_3} x ds
=
\frac{l_{35}}{2} (x_3 + x_5)
\]
\[
\int_{s_5}^{s_3} x^2 ds
=
\frac{l_{35}}{3}
(
x_3^2 + x_3 x_5 + x_5^2
)
\]
\[
\int_{s_5}^{s_3} xy ds
=
\frac{l_{35}}{6}
(
2 x_3 y_3
+ x_3 y_5
+ x_5 y_3
+ 2 x_5 y_5
)
\]
\[
\int_{s_5}^{s_3} y ds
=
\frac{l_{35}}{2} (y_3 + y_5)
\]
\[
\int_{s_5}^{s_3} y^2 ds
=
\frac{l_{35}}{3}
(
y_3^2 + y_3 y_5 + y_5^2
)
\]
前節で求めた積分公式を用いて初めに示した面内平面要素の剛性行列を表す.
\[
\left\{
\begin{array}{l}
K_{11} = k_n y_{35}^2 + k_s x_{35}^2 \\
K_{12} = -(k_n-k_s) y_{35}x_{35} \\
K_{13} = -k_ny_{35} \Delta_{11} + k_s x_{35}\Delta_{21} \\
K_{14} = -K_{11} \\
K_{15} = -K_{12} \\
K_{16} = -k_ny_{35} \Delta_{22} + k_s x_{35}\Delta_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{22} = k_n x_{35}^2 + k_s y_{35}^2 \\
K_{23} = k_nx_{35} \Delta_{11} + k_s y_{35}\Delta_{21} \\
K_{24} = -K_{12} \\
K_{25} = -K_{22} \\
K_{26} = k_nx_{35} \Delta_{22} + k_s y_{35}\Delta_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{33} = k_n \Delta_{11}^2 + k_s \Delta_{21}^2 + k_n l_{35}^4/12\\
K_{34} = -K_{13} \\
K_{35} = -K_{23} \\
K_{36} = k_n \Delta_{11} \Delta_{22}
+ k_s \Delta_{21} \Delta_{12}
- k_n l_{35}^4/12
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{44} = K_{11} \\
K_{45} = K_{12} \\
K_{46} =-K_{16}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{55} = K_{22} \\
K_{56} =-K_{26}
\end{array}
\right.
\]
\[
K_{66} = k_n \Delta_{22}^2
+ k_s \Delta_{12}^2
+ k_n l_{35}^4/12
\]
\[\hspace{10em}
\left( \times 1/l_{35} \right)
\]
\[
\left\{
\begin{array}{l}
2 \Delta_{11} = x_{35}(x_{31}+x_{51})
+ y_{35}(y_{31}+y_{51}) \\
2 \Delta_{12} = x_{35}(y_{32}+y_{52})
- y_{35}(x_{32}+x_{52}) \\
2 \Delta_{21} =-x_{35}(y_{31}+y_{51})
+ y_{35}(x_{31}+x_{51}) \\
2 \Delta_{22} =-x_{35}(x_{32}+x_{52})
- y_{35}(y_{32}+y_{52})
\end{array}
\right.
\]
\[
\left(
x_{ij} = x_i - x_j ,
y_{ij} = y_i - y_j
\right)
\]
いま,塑性化後のばね行列を $\boldsymbol{D}^{(p)}$ とすると
\[
\boldsymbol{D}^{(p)} =
\left[
\begin{array}{cc}
D_{11} & D_{12} \\
D_{21} & D_{22}
\end{array}
\right]
\]
と表せる.このときの剛性行列の成分は以下のように与えられる.
\[
\left\{
\begin{array}{l}
K_{11} = D_{11} y_{35}^2 + D_{22} x_{35}^2
+ 2 x_{35} y_{35} D_{12} \\
K_{12} = -(D_{11}-D_{22}) y_{35}x_{35}
+ (y_{35}^2 - x_{35}^2) D_{12} \\
K_{13} = -D_{11} y_{35} \Delta_{11} + D_{22} x_{35}\Delta_{21}
- (x_{35} \Delta_{11} - y_{35} \Delta_{21}) D_{12} \\
K_{14} = -K_{11} \\
K_{15} = -K_{12} \\
K_{16} = -D_{11} y_{35} \Delta_{22} + D_{22} x_{35}\Delta_{12}
- (x_{35} \Delta_{22} - y_{35} \Delta_{12} ) D_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{22} = D_{11} x_{35}^2 + D_{22} y_{35}^2
- 2 x_{35} y_{35} D_{12} \\
K_{23} = k_nx_{35} \Delta_{11} + k_s y_{35}\Delta_{21}
- (x_{35} \Delta_{21} + y_{35} \Delta_{11} ) D_{12} \\
K_{24} = -K_{12} \\
K_{25} = -K_{22} \\
K_{26} = k_nx_{35} \Delta_{22} + k_s y_{35}\Delta_{12}
- (x_{35} \Delta_{12} + y_{35} \Delta_{22} ) D_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{33} = k_n \Delta_{11}^2 + k_s \Delta_{21}^2 + k_n l_{35}^4/12
- 2 \Delta_{11} \Delta_{12} D_{21}\\
K_{34} = -K_{13} \\
K_{35} = -K_{23} \\
K_{36} = k_n \Delta_{11} \Delta_{22}
+ k_s \Delta_{21} \Delta_{12}
- k_n l_{35}^4/12
- ( \Delta_{11} \Delta_{12} + \Delta_{21} \Delta_{22} ) D_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{44} = K_{11} \\
K_{45} = K_{12} \\
K_{46} =-K_{16}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{55} = K_{22} \\
K_{56} =-K_{26}
\end{array}
\right.
\]
\[
K_{66} = k_n \Delta_{22}^2
+ k_s \Delta_{12}^2
+ k_n l_{35}^4/12
- 2 \Delta_{12} \Delta_{22} D_{12}
\]
\[\hspace{15em}
\left( \times 1/l_{35} \right)
\]
このように,
7.3節 で示した弾性時の剛性行列とほとんど変わらな.塑性化後の剛性行列は,弾性時の剛性行列に非対角項 $D_{12}$ の効果が加えられているだけである.