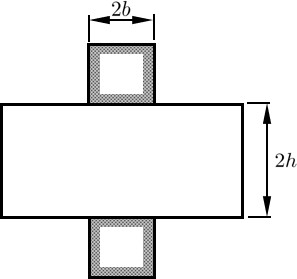
剛塑性体における平面ひずみ問題の例に,よく知られているブロツクの圧縮とポンチの押し込み問題がある.一般に,金属板より圧縮板の幅が大きいときその問題はブロックの圧縮問題として解析され,その逆の場合はポンチの押し込み問題として解析される.
本節では
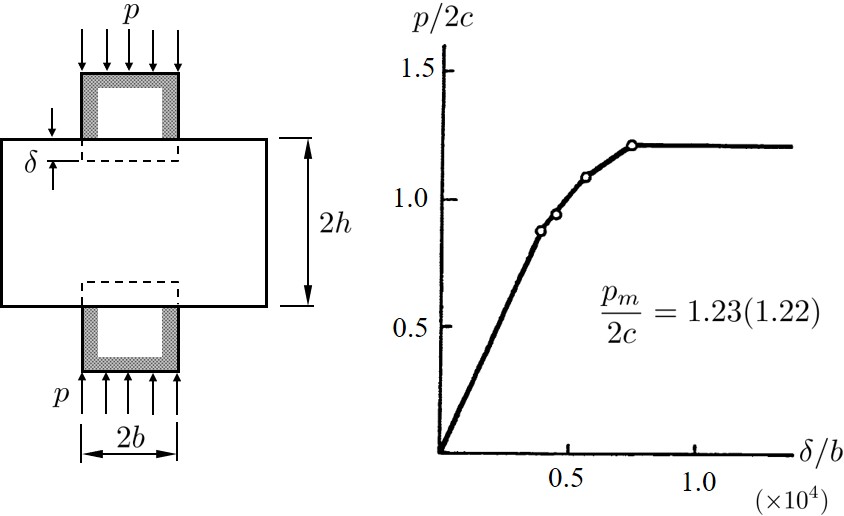
図6.1 に示すポンチの押し込み問題に対する数値計算例を示す.ポンチの押し込み問題は解析的に考えると,ブロツクの圧縮問題と異なり,一様な圧縮応力場と剛塑性域の境界上で速度の不連続がゆるされず,取り扱いが面倒になる.しかし,数値計算では境界条件以外の差はほとんど無く,構造が複雑になればなるほど解析的手法に比べ成力を発揮する.
$\hspace{1em}$図6.1 ポンチの押し込み問題
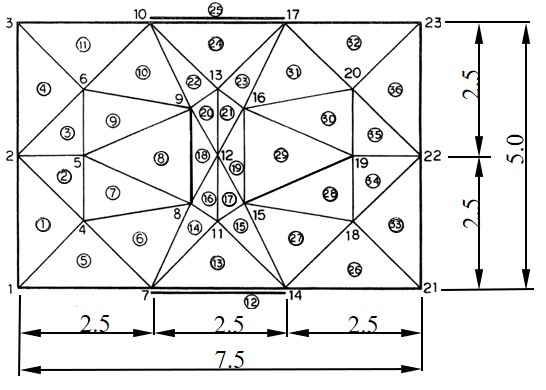
本書で用いた寸法及び要素分割を
図6.2 に示す.この例題では2h = 5cm, 2b = 2.5cm, h/b = 2であり,このときの極限荷重は解析的に
\[
\frac{p_m}{2c} = 1.22
\]
と得られる.ここで が載荷面上における単位面積当りの極限荷重である.節点数が23節点,要素数が36要素で,総自由度数は境界を含め108自由度である.支点条件用の境界要素として⑫要素を設定し,また載荷処理用として㉕要素を設定している.この2つの要素は先にも説明したように厚さの無い,自由度のみ持つ要素である.
$\hspace{3em}$図6.2 要素分割例(単位:cm)
破壊条件としてはクーロンの条件を用い,材料定数を
表6.1 に示すよう仮定した.また,本例題では自重を無視している.
表6.1 材料定数
弾性係数 $(E)$
$200 {\rm GPa}$ ポアソン比 $(\nu)$
0.3 せん断強さ $(c)$
$3 {\rm MPa}$ 内部摩擦角 $(\phi)$
$0^{\circ}$
上記の条件を基に作成されたサンプル・プログラム用のデータが
図6.3 に示されている.境界条件としては⑫要素を固定し,荷重条件としては㉕要素に $1000 {\rm kN}$ の外力を与えている.
\[
P = 1000 \; {\rm kN} \;\;\;\;
\left( p = \frac{P}{2b} = 4 \; {\rm MPa} \right)
\]
ここでは,崩壊時の極限荷重を求めるため,理論解より大きい荷重を入力している.
----+----1----+----2-----
10
23
1 0. 0.
2 0. 0.025
3 0. 0.05
4 0.0125 0.0125
5 0.0125 0.025
6 0.0125 0.0375
7 0.025 0.
8 0.0325 0.016
9 0.0325 0.034
10 0.025 0.05
11 0.0375 0.0125
12 0.0375 0.025
13 0.0375 0.0375
14 0.05 0.
15 0.0425 0.016
16 0.0425 0.034
17 0.05 0.05
18 0.0625 0.0125
19 0.0625 0.025
20 0.0625 0.0375
21 0.075 0.
22 0.075 0.025
23 0.075 0.05
36 0
1 1 2 1 4
2 1 2 4 5
3 1 2 5 6
4 1 6 3 2
5 1 1 7 4
6 1 4 7 8
7 1 5 4 8
8 1 8 9 5
9 1 6 5 9
10 1 9 10 6
11 1 10 3 6
12 1 14 7 0
13 1 7 14 11
14 1 8 7 11
15 1 14 15 11
16 1 8 11 12
17 1 12 11 15
18 1 9 8 12
19 1 15 16 12
20 1 9 12 13
21 1 13 12 16
22 1 10 9 13
23 1 13 16 17
24 1 17 10 13
25 1 10 17 0
26 1 14 21 18
27 1 15 14 18
28 1 18 19 15
29 1 16 15 19
30 1 16 19 20
31 1 17 16 20
32 1 17 20 23
33 1 22 18 21
34 1 22 19 18
35 1 20 19 22
36 1 23 20 22
1
1 200000000. 0.3 0. 3000. 0. 1.
1
1 25 0. -1000. 0.
3
1 12 1
2 12 2
3 12 3
----+----1----+----2-----
$\hspace{2em}$図6.3 入力データ例
図6.4 ~
図6.11 は本書のサンプル・プログラムによる入力情報の出力結果である.
図6.4 は基本データに関する情報を出力したもので,要素夕イプは平面ひずみであり,プログラム内部で作成されたばねデータの数は48である.また,メカニズム・チェック用の最大変位は1000としており,最大バンド幅は39である.
TITLE : TEST DATA
INFORMATION :
ELEMET TYPE ------------------> PLANE STRAIN
NUMBER OF NODE ---------------> 23
NUMBER OF ELEMENTS -----------> 36
NUMBER OF MATERIALS ----------> 1
NUMBER OF SPRINGS ------------> 48
NUMBER OF LOADS --------------> 1
NUMBER OF SUPPORT D.O.F. -----> 3
MAXIMUM BAND WIDTH -----------> 39
NUMBER OF ITARATIONS ---------> 10
MAXIMUM DISPLACEMENT ---------> 0.1E+04
$\hspace{2em}$図6.4 入力情報の出力結果
図6.5 は入力した座標値を出力したものである.
COORDINATE DATA :
NODE NO. X-COORDINATE Y-COORDINATE
1 0.00000E+00 0.00000E+00
2 0.00000E+00 0.25000E-01
3 0.00000E+00 0.50000E-01
4 0.12500E-01 0.12500E-01
5 0.12500E-01 0.25000E-01
6 0.12500E-01 0.37500E-01
7 0.25000E-01 0.00000E+00
8 0.32500E-01 0.16000E-01
9 0.32500E-01 0.34000E-01
10 0.25000E-01 0.50000E-01
11 0.37500E-01 0.12500E-01
12 0.37500E-01 0.25000E-01
13 0.37500E-01 0.37500E-01
14 0.50000E-01 0.00000E+00
15 0.42500E-01 0.16000E-01
16 0.42500E-01 0.34000E-01
17 0.50000E-01 0.50000E-01
18 0.62500E-01 0.12500E-01
19 0.62500E-01 0.25000E-01
20 0.62500E-01 0.37500E-01
21 0.75000E-01 0.00000E+00
22 0.75000E-01 0.25000E-01
23 0.75000E-01 0.50000E-01
$\hspace{2em}$図6.5 座標データの出力結果
図6.6 は要素に関係するデー夕の出力結果である.出力内容は左からの順に表示されている.要素構成節点番号(1)(2)(3)は先に示したように,三角形の頂点に関する節点番号を左回りに読み込んだデータである.なお,境界用の要素については3番目の要素構成節点番号を0とし,また,要素面積も0としている.
要素番号
要素構成節点番号(1)(2)(3)
材料種類番号(MAT.NO.)
要素面積(AREA)
x方向図心座標(XG)
y方向図心座標(YG)
ELEMENT DATA :
ELEM.NO. (1) (2) (3) MAT.NO. AREA XG YG
1 2 1 4 1 0.15625E-03 0.41667E-02 0.12500E-01
2 2 4 5 1 0.78125E-04 0.83333E-02 0.20833E-01
3 2 5 6 1 0.78125E-04 0.83333E-02 0.29167E-01
4 6 3 2 1 0.15625E-03 0.41667E-02 0.37500E-01
5 1 7 4 1 0.15625E-03 0.12500E-01 0.41667E-02
6 4 7 8 1 0.14688E-03 0.23333E-01 0.95000E-02
7 5 4 8 1 0.12500E-03 0.19167E-01 0.17833E-01
8 8 9 5 1 0.18000E-03 0.25833E-01 0.25000E-01
9 6 5 9 1 0.12500E-03 0.19167E-01 0.32167E-01
10 9 10 6 1 0.14688E-03 0.23333E-01 0.40500E-01
11 10 3 6 1 0.15625E-03 0.12500E-01 0.45833E-01
12 14 7 0 1 0.00000E+00 0.37500E-01 0.00000E+00
13 7 14 11 1 0.15625E-03 0.37500E-01 0.41667E-02
14 8 7 11 1 0.53125E-04 0.31667E-01 0.95000E-02
15 14 15 11 1 0.53125E-04 0.43333E-01 0.95000E-02
16 8 11 12 1 0.31250E-04 0.35833E-01 0.17833E-01
17 12 11 15 1 0.31250E-04 0.39167E-01 0.17833E-01
18 9 8 12 1 0.45000E-04 0.34167E-01 0.25000E-01
19 15 16 12 1 0.45000E-04 0.40833E-01 0.25000E-01
20 9 12 13 1 0.31250E-04 0.35833E-01 0.32167E-01
21 13 12 16 1 0.31250E-04 0.39167E-01 0.32167E-01
22 10 9 13 1 0.53125E-04 0.31667E-01 0.40500E-01
23 13 16 17 1 0.53125E-04 0.43333E-01 0.40500E-01
24 17 10 13 1 0.15625E-03 0.37500E-01 0.45833E-01
25 10 17 0 1 0.00000E+00 0.37500E-01 0.50000E-01
26 14 21 18 1 0.15625E-03 0.62500E-01 0.41667E-02
27 15 14 18 1 0.14687E-03 0.51667E-01 0.95000E-02
28 18 19 15 1 0.12500E-03 0.55833E-01 0.17833E-01
29 16 15 19 1 0.18000E-03 0.49167E-01 0.25000E-01
30 16 19 20 1 0.12500E-03 0.55833E-01 0.32167E-01
31 17 16 20 1 0.14688E-03 0.51667E-01 0.40500E-01
32 17 20 23 1 0.15625E-03 0.62500E-01 0.45833E-01
33 22 18 21 1 0.15625E-03 0.70833E-01 0.12500E-01
34 22 19 18 1 0.78125E-04 0.66667E-01 0.20833E-01
35 20 19 22 1 0.78125E-04 0.66667E-01 0.29167E-01
36 23 20 22 1 0.15625E-03 0.70833E-01 0.37500E-01
$\hspace{2em}$図6.6 要素デー夕の出力結果
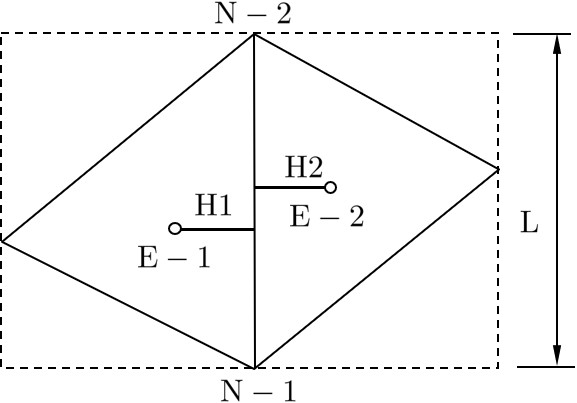
図6.7 はプログラム内部で作成したばね関係のデータであり,記号については
図6.8 に示されている.出力内容は左から以下の順に表示されている.
ばね番号
ばね構成要素番号(E-1)(E-2)
ばね構成節点番号(N-1)(N-2)
SPRING DATA :
SPRG.NO. E-1 E-2 N-1 N-2 L H1 H2
1 1 2 4 2 0.17678E-01 0.58926E-02 0.29463E-02
2 1 5 1 4 0.17678E-01 0.58926E-02 0.58926E-02
3 2 3 5 2 0.12500E-01 0.41667E-02 0.41667E-02
4 2 7 4 5 0.12500E-01 0.41667E-02 0.66667E-02
5 3 4 6 2 0.17678E-01 0.29463E-02 0.58926E-02
6 3 9 5 6 0.12500E-01 0.41667E-02 0.66667E-02
7 4 11 6 3 0.17678E-01 0.58926E-02 0.58926E-02
8 5 6 7 4 0.17678E-01 0.58926E-02 0.55390E-02
9 6 7 8 4 0.20304E-01 0.48225E-02 0.41043E-02
10 6 14 7 8 0.17671E-01 0.55412E-02 0.20043E-02
11 7 8 8 5 0.21932E-01 0.37997E-02 0.54715E-02
12 8 9 9 5 0.21932E-01 0.54715E-02 0.37997E-02
13 8 18 8 9 0.18000E-01 0.66667E-02 0.16667E-02
14 9 10 9 6 0.20304E-01 0.41043E-02 0.48225E-02
15 10 11 10 6 0.17678E-01 0.55390E-02 0.58926E-02
16 10 22 9 10 0.17671E-01 0.55412E-02 0.20043E-02
17 12 13 14 7 0.25000E-01 0.00000E+00 0.41667E-02
18 13 14 11 7 0.17678E-01 0.58926E-02 0.20035E-02
19 13 15 14 11 0.17678E-01 0.58926E-02 0.20035E-02
20 14 16 11 8 0.61033E-02 0.58029E-02 0.34135E-02
21 15 17 15 11 0.61033E-02 0.58029E-02 0.34135E-02
22 15 27 14 15 0.17671E-01 0.20043E-02 0.55412E-02
23 16 17 11 12 0.12500E-01 0.16667E-02 0.16667E-02
24 16 18 12 8 0.10296E-01 0.20235E-02 0.29139E-02
25 17 19 15 12 0.10296E-01 0.20235E-02 0.29139E-02
26 18 20 12 9 0.10296E-01 0.29139E-02 0.20235E-02
27 19 21 16 12 0.10296E-01 0.29139E-02 0.20235E-02
28 19 29 15 16 0.18000E-01 0.16667E-02 0.66667E-02
29 20 21 12 13 0.12500E-01 0.16667E-02 0.16667E-02
30 20 22 13 9 0.61033E-02 0.34135E-02 0.58029E-02
31 21 23 16 13 0.61033E-02 0.34135E-02 0.58029E-02
32 22 24 13 10 0.17678E-01 0.20035E-02 0.58926E-02
33 23 24 17 13 0.17678E-01 0.20035E-02 0.58926E-02
34 23 31 16 17 0.17671E-01 0.20043E-02 0.55412E-02
35 24 25 17 10 0.25000E-01 0.41667E-02 0.00000E+00
36 26 27 18 14 0.17678E-01 0.58926E-02 0.55390E-02
37 26 33 21 18 0.17678E-01 0.58926E-02 0.58926E-02
38 27 28 18 15 0.20304E-01 0.48225E-02 0.41043E-02
39 28 29 19 15 0.21932E-01 0.37997E-02 0.54715E-02
40 28 34 18 19 0.12500E-01 0.66667E-02 0.41667E-02
41 29 30 19 16 0.21932E-01 0.54715E-02 0.37997E-02
42 30 31 20 16 0.20304E-01 0.41043E-02 0.48225E-02
43 30 35 19 20 0.12500E-01 0.66667E-02 0.41667E-02
44 31 32 20 17 0.17678E-01 0.55390E-02 0.58926E-02
45 32 36 20 23 0.17678E-01 0.58926E-02 0.58926E-02
46 33 34 22 18 0.17678E-01 0.58926E-02 0.29463E-02
47 34 35 22 19 0.12500E-01 0.41667E-02 0.41667E-02
48 35 36 22 20 0.17678E-01 0.29463E-02 0.58926E-02
$\hspace{2em}$図6.7 ばねデー夕の出力結果
$\hspace{3em}$図6.8 ばねデー夕に関する記号
図6.9 は材料デー夕であり,対応している出力内容は左から以下の順で表示されている.本例題では平面ひずみを仮定しているため,解析板厚を1としている.
材料種類番号
弾性係数(E)
ポアソン比(P)
物体力(BODY FORCE)
せん断強さ(C)
内部摩擦角(PHI)
解析板厚(t)
MATERIAL DATA :
MAT.NO. E P BODY FORCE C PHI t
1 0.20000E+09 0.30000E+00 0.00000E+00 0.30000E+04 0.00000E+00 0.10000E+01
$\hspace{2em}$図6.9 材料デー夕の出力結果
図6.10 は載荷デー夕で載荷要素番号の他,載荷値が以下のように出力される.
荷重番号
載荷要素番号
荷重値(X)
荷重値(Y)
荷重値(M)
LOAD DATA :
NO. ELEM.NO. X Y M
1 25 0.000E+00 -0.100E+04 0.000E+00
$\hspace{2em}$図6.10 荷重デー夕の出力結果
図6.11 は支点条件で,上から $x$ 方向拘束要素番号,$y$ 方向拘束要素番号,$\theta$ 回転拘束要素番号を示している.本例題では⑫要素に対し,$(u,v,\theta)$ の自由度を拘束している.
SUPPORT D.O.F.:
NO. ELEM.NO. DIREC.
1 12 1
2 12 2
3 12 3
$\hspace{2em}$図6.11 支点デー夕の出力結果
本節では
6.1節 で説明したデータを基に,本サンプル・プログラムにより解析した結果を示す.
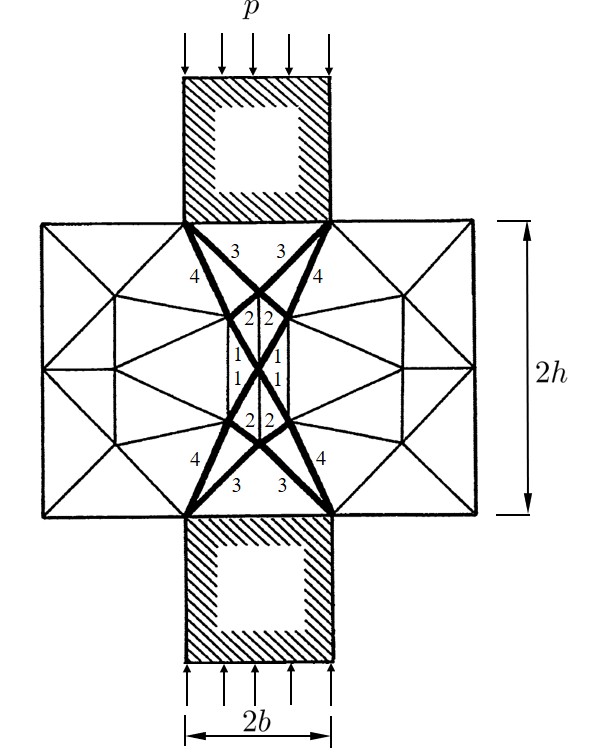
RBSMを用いた離散化極限解析における特徴の1つはすべり線が得られることである.従来の有限要素法では,降伏した要素を塗りつぶしたりすることによって塑性化領域を表現していたが,すべり線の場合は要素自身ではなく,要素境界辺の塑性化であるため,有限要素法とは表現方法が異なる.いろいろな表現方法が考えられるが,本書では太線によりすべり線を表現している.
図6.12 は本例題に関するすべり線の発達状況を表したものである.図中の数字はすべりの発生した荷重増分ステップ番号を示している.
$\hspace{2em}$図6.12 すべり線の発達状況
計算された荷重増分率及び載荷荷重が
表6.2 に整理されている.$p$ は作用荷重値 $(P)$ を載荷幅 $2.5 {\rm cm}$ で割つた単位面積当りの値である.また,表の最後に示した $p/2c$ は単位面積当りの載荷荷重をせん断強さにより無次元化した値である.
表6.2 荷重増分率と載荷荷重
荷重増分ステップ
$r_{\rm min}$
$p ({\rm MPa})$
$p/2c$
1
0.14256
5.7024
0.95 2
0.15376
6.1504
1.02 3
0.1642
6.5768
1.10 4
0.18526
7.4104
1.23
一方,変位については載荷板の変位 $\delta$ を
図6.13(a) に示すようにとり,載荷幅の半分 $b$ により無次元化を行う.このように無次元化された載荷荷重と変位により載荷-変位曲線を描いたものが
図6.13(b) に示されている.解析解が $(p/2c = 1.22)$ で,計算による解が $(p/2c = 1,23)$であり,約1%程度の誤差で極限荷重が求められている.
$\hspace{1em}$(a)載荷板の変位 $(\delta)$
$\hspace{6em}$(b)荷重-変位曲線図6.13 すべり線の発達状況
最後に出力結果に対する説明を行う.荷重増分計算の場合,繰り返し計算が必要であり,繰り返し回数が多くなれば,それに伴い出力量も増える.本例題では4回の操り返し計算により崩壊荷重が得られている.したがって,出力は4ステップ分の量があるが,ここでは,最終ステップのみ取り上げ,説明を行う.
図6.14 は各計算ステップにおける荷重増分率の値であり,出力は左から以下のような内容となっている.
STEP NO.= 荷重増分ステップ番号
STEP = 今回の荷重増分率
RMIN = 累積荷重増分率
例題の出力では4ステップ目の荷重増分率が $0.020843で$,今回迄の累積荷重増分率が $0.l8526$ となっている.本例題では㉕要素に $1000{\rm kN}$ の外力を与えているため,4ステップ迄に作用した全荷重は
\[
P_4 = P \times r_{\rm min} = 1000 \times 0.18526 = 185.26 \; {\rm kN}
\]
となる.例題では $2b=2.5 {\rm cm}$ であるから,単位面積当りの荷重は
\[
p_4 = P_4 / 2b = 7.4104 \; {\rm MPa}
\]
となり,$p/2c=1.23$ が求められる.
OUTPUT DATA :
STEP NO.= 4 STEP = 0.20843E-01 RMIN = 0.18526E+00
$\hspace{2em}$図6.14 荷重増分率の出力結果
図6.15 は変位に関する出力結果である.結果は
の順に表示される.単位は入力された単位系を採用している.
< DISPLACEMENT >
ELEM.NO. U V T
1 -0.18932E-06 -0.93465E-06 -0.84964E-05
2 -0.25413E-06 -0.90764E-06 -0.56882E-05
3 -0.25413E-06 -0.94281E-06 0.56882E-05
4 -0.18932E-06 -0.91581E-06 0.84964E-05
5 -0.10952E-06 -0.83835E-06 -0.11964E-04
6 -0.18047E-06 -0.69563E-06 -0.14106E-04
7 -0.23824E-06 -0.82900E-06 -0.52235E-05
8 -0.18870E-06 -0.92523E-06 0.17881E-18
9 -0.23824E-06 -0.10215E-05 0.52235E-05
10 -0.18047E-06 -0.11548E-05 0.14106E-04
11 -0.10952E-06 -0.10121E-05 0.11964E-04
12 0.00000E+00 0.00000E+00 0.00000E+00
13 -0.12384E-21 -0.11468E-06 -0.13893E-19
14 -0.16650E-06 -0.43699E-06 -0.73944E-05
15 0.16650E-06 -0.43699E-06 0.73944E-05
16 -0.83037E-08 -0.68908E-06 -0.46589E-06
17 0.83037E-08 -0.68908E-06 0.46589E-06
18 -0.13915E-06 -0.92523E-06 0.12481E-18
19 0.13915E-06 -0.92523E-06 0.30687E-19
20 -0.83037E-08 -0.11614E-05 0.46589E-06
21 0.83037E-08 -0.11614E-05 -0.46589E-06
22 -0.16650E-06 -0.14135E-05 0.73944E-05
23 0.16650E-06 -0.14135E-05 -0.73944E-05
24 0.47928E-20 -0.17358E-05 0.13809E-18
25 0.53720E-20 -0.18505E-05 0.14672E-18
26 0.10952E-06 -0.83835E-06 0.11964E-04
27 0.18047E-06 -0.69563E-06 0.14106E-04
28 0.23824E-06 -0.82900E-06 0.52235E-05
29 0.18870E-06 -0.92523E-06 -0.10252E-19
30 0.23824E-06 -0.10215E-05 -0.52235E-05
31 0.18047E-06 -0.11548E-05 -0.14106E-04
32 0.10952E-06 -0.10121E-05 -0.11964E-04
33 0.18932E-06 -0.93465E-06 0.84964E-05
34 0.25413E-06 -0.90764E-06 0.56882E-05
35 0.25413E-06 -0.94281E-06 -0.56882E-05
36 0.18932E-06 -0.91581E-06 -0.84964E-05
$\hspace{2em}$図6.15 変位の出力結果
次に,単位面積当りの表面力と仮想ひずみ及び降伏判定フラッグを
図6.16 に示す.ただし,出力内容は左から以下のようになっており,降伏しているばねのフラッグは1となっている.
ばね番号
降伏判定フラッグ(YIELD)
垂直応力 SIG-N
せん断応力 TAU-S
垂直ひずみ EPS-N
せん断ひずみGAM-S
ここで,ひずみは,単位長さあたりの相対変位のことである.
< STRESS & STRAIN >
SPRING.NO. YIELD SIG-N TAU-S EPS-N GAM-S
1 0 -0.51704E+02 -0.33083E+02 -0.19204E-06 -0.21504E-06
2 0 -0.33083E+02 0.51704E+02 -0.12288E-06 0.33608E-06
3 0 -0.37052E+03 -0.23243E-11 -0.13762E-05 -0.15108E-19
4 0 -0.18621E+02 0.28573E+03 -0.69164E-07 0.18573E-05
5 0 -0.51704E+02 0.33083E+02 -0.19204E-06 0.21504E-06
6 0 -0.18621E+02 -0.28573E+03 -0.69164E-07 -0.18573E-05
7 0 -0.33083E+02 -0.51704E+02 -0.12288E-06 -0.33608E-06
8 0 0.51704E+02 0.33083E+02 0.19204E-06 0.21504E-06
9 0 -0.32409E+04 -0.16493E+03 -0.12038E-04 -0.10721E-05
10 1 -0.23068E+04 0.30000E+04 -0.85682E-05 0.19500E-04
11 0 -0.22530E+04 -0.17343E+04 -0.83684E-05 -0.11273E-04
12 0 -0.22530E+04 0.17343E+04 -0.83684E-05 0.11273E-04
13 0 0.16010E+04 -0.17846E-12 0.59466E-05 -0.11600E-20
14 0 -0.32409E+04 0.16493E+03 -0.12038E-04 0.10721E-05
15 0 0.51704E+02 -0.33083E+02 0.19204E-06 -0.21504E-06
16 1 -0.23068E+04 -0.30000E+04 -0.85682E-05 -0.19500E-04
17 0 -0.74104E+04 0.24352E-11 -0.27524E-04 0.15829E-19
18 1 -0.44104E+04 0.30000E+04 -0.16381E-04 0.41897E-04
19 1 -0.44104E+04 -0.30000E+04 -0.16381E-04 -0.41897E-04
20 1 -0.33656E+04 -0.30000E+04 -0.12501E-04 -0.34575E-04
21 1 -0.33656E+04 0.30000E+04 -0.12501E-04 0.34575E-04
22 1 -0.23068E+04 -0.30000E+04 -0.85682E-05 -0.19500E-04
23 0 0.14104E+04 -0.94466E-11 0.52385E-05 -0.61403E-19
24 1 -0.65647E+02 0.30000E+04 -0.24383E-06 0.54489E-04
25 1 -0.65647E+02 -0.30000E+04 -0.24383E-06 -0.54489E-04
26 1 -0.65647E+02 -0.30000E+04 -0.24383E-06 -0.54489E-04
27 1 -0.65647E+02 0.30000E+04 -0.24383E-06 0.54489E-04
28 0 0.16010E+04 0.62612E-11 0.59466E-05 0.40698E-19
29 0 0.14104E+04 -0.36529E-11 0.52385E-05 -0.23744E-19
30 1 -0.33656E+04 0.30000E+04 -0.12501E-04 0.34575E-04
31 1 -0.33656E+04 -0.30000E+04 -0.12501E-04 -0.34575E-04
32 1 -0.44104E+04 -0.30000E+04 -0.16381E-04 -0.41897E-04
33 1 -0.44104E+04 0.30000E+04 -0.16381E-04 0.41897E-04
34 1 -0.23068E+04 0.30000E+04 -0.85682E-05 0.19500E-04
35 0 -0.74104E+04 -0.14341E-12 -0.27524E-04 -0.93213E-21
36 0 0.51704E+02 -0.33083E+02 0.19204E-06 -0.21504E-06
37 0 -0.33083E+02 -0.51704E+02 -0.12288E-06 -0.33608E-06
38 0 -0.32409E+04 0.16493E+03 -0.12038E-04 0.10721E-05
39 0 -0.22530E+04 0.17343E+04 -0.83684E-05 0.11273E-04
40 0 -0.18621E+02 -0.28573E+03 -0.69164E-07 -0.18573E-05
41 0 -0.22530E+04 -0.17343E+04 -0.83684E-05 -0.11273E-04
42 0 -0.32409E+04 -0.16493E+03 -0.12038E-04 -0.10721E-05
43 0 -0.18621E+02 0.28573E+03 -0.69164E-07 0.18573E-05
44 0 0.51704E+02 0.33083E+02 0.19204E-06 0.21504E-06
45 0 -0.33083E+02 0.51704E+02 -0.12288E-06 0.33608E-06
46 0 -0.51704E+02 0.33083E+02 -0.19204E-06 0.21504E-06
47 0 -0.37052E+03 -0.38112E-11 -0.13762E-05 -0.24773E-19
48 0 -0.51704E+02 -0.33083E+02 -0.19204E-06 -0.21504E-06
$\hspace{2em}$図6.16 応力,ひずみ及び降伏判定フラッグの出力結果
本例題では内部摩擦角を0としているため,破壊は垂直応力の如何に関わらず,せん断応力がせん断強度 $c$ に達した段階で生じている.すなわち,すべり破壊しているばねでは降伏判定フラッグが1となり,せん断力の項が±30と表示されている.
ばねが降伏し,構造が崩壊機構条件を満たすと,最終的に連立方程式を解くことができなくなる.この時点で構造物は崩壊したとしてメッセージを出力して計算を終了させる.一方,計算誤差などの関係により,メカニズムに達していながら変位が求まってしまうこともある.しかし,それ以後の計算には意味が無いので,許容値以上の変位が生じていたならば
図6.17 に示すよう,計算された最大変位と許容値を出力し,計算を終了させる.ただし,局所破壊などのように,部分的にメカニズムを形成した場合も同様なメッセージが出力され計算が終了してしまうので注意が必要である.
********************************************
COLLAPS !! DMAX = 0.42280E+10 ( 0.10000E+04 )
********************************************
$\hspace{2em}$図6.17 変位が大きくなった場合のメカニズム・メッセージ