5.離散化解極限解析の変位・表面力計算
- 5-1 プログラム構造
- 5-2 ばね係数の作成
- 5-3 構成行列の作成
- 5-4 ばね剛性行列の作成
- 5-5 全体剛性行列の作成
- 5-6 表面力の計算
- 5-7 除荷・負荷の判定
- 5-8 荷重増分率の計算
- 5-9 全体剛性行列の作成
5-1 プログラム構造
RBSMを理解する上で弾性解析用のプログラム作成することは重要ではあるが,本来,RBSMは極限解析用のモデルであり,その特徴を理解するためには非線形解析法を含めた形で考えてゆかなければならない.したがって,ある程度FEMで非線形解析のプログラムを作成した経験があった方がより理解しやすいが,そのような経験がなくてもかまわない.さて,本書におけるサンプル・プログラムは
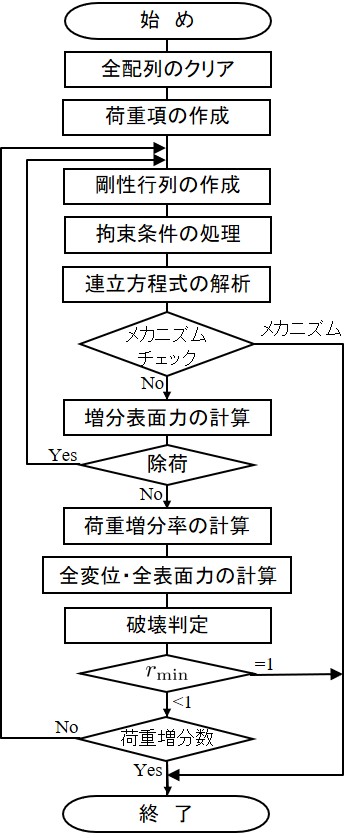
一方,離散化極限解析では各種の判定や,荷重増分に伴ういくつかの繰り返し計算が必要となる.図に示す荷重増分に関するループは本来なくてもよいもので,$r_{\rm min}$ が1になるまで繰り返し計算を行つていればよい.このようなループを設けた理由は がなかなか1にならない場合に計算が暴走するのを防ぐためである.
次に,剛性行列を解いて変位を求めるが,剛性行列の作成ではすべりの生じたばねとそうでないばねと分けて考える必要がある.また,得られた変位は仮の増分変位で,実際には荷重増分率がかかった値が今回の増分変位となる.これは,
構造物が崩壊機構を形成すれば,連立方程式が解けなくなり,計算を終了させることができるが,そのような状態に至らないまでも変位が急増し,その後の計算にあまり意味がないような場合には計算を強制的に終了させた方がよい.このようなメカニズム・チェックの方法には最大変位を調べる方法や,荷重変位曲線の勾配を調べる方法などがあるが,本サンプル・プログラムでは前者の最大変位をチェックしている.この方法を用いる場合は $r_{\rm min}$ 倍された後の全変位で行わない方がよい.これは,仮の増分変位が大きくても荷重増分率が極端に小さいと,両者を掛け合わせた今回の増分変位が小さくなり,前回の変位に増分変位を加えた全変位が前回とあまり変わらなくなるためである.崩壊荷重時近傍ではこのような現象がたびたび生じるため,メカニズム・ チェックは何らかの方法で必ず組み込んでおいた方がよいであろう.
非線形解析のもう一つの特徴として,除荷,負荷がある.この過程を設けていないと崩壊荷重や極限荷重が実際と異なって求まることがある.特にRBSMではばねを切断したりするため,除荷を認めておかないと,除荷が発生した場合,本来と異なった構造を解いていることになる.通常の単調載荷の場合にはあまり除荷は発生しないが,得られる解の信頼性を増すためにもこの過程は組み込んでおく必要がある.なお,本プログラムでは除荷発生後,ばねを弾性状態に戻して再計算を行うようにしている.
最後に,荷重増分率を計算し,全変位及び全表面力を求め,それを今回の値として破壊状態を調べる.荷重増分率の累計が1になったら,全荷重が作用し終わったものとして計算を終了させる.荷重増分率が1以下ならさらに載荷を行い上記と同様な手順を繰り返す.
このような計算の流れをプログラム化したものが
524 !=============================================================================== 525 SUBROUTINE Analysis( Node, Element, Material, Spring, Load, Boundary, & 526 Nonlinear, Solver, File) 527 528 TYPE(typeNode), INTENT(IN) :: Node 529 TYPE(typeElement), INTENT(INOUT) :: Element 530 TYPE(typeMaterial), INTENT(IN) :: Material 531 TYPE(typeSpring), INTENT(INOUT) :: Spring 532 TYPE(typeLoad), INTENT(IN) :: Load 533 TYPE(typeBoundary), INTENT(IN) :: Boundary 534 TYPE(typeNonLinear),INTENT(INOUT) :: NonLinear 535 TYPE(typeBand), INTENT(INOUT) :: Solver 536 TYPE(typeFile), INTENT(IN) :: File 537 538 INTEGER :: iste,jramc,jramd,error 539 540 Nonlinear%rmin = 0.D0 541 CALL ClearArray(Element,Spring) 542 CALL formLoad(Element,Material,Load) 543 iste = 0 544 Iteration : DO WHILE(.TRUE.) 545 iste = iste + 1 546 jramc = 0 547 jramd = 1 548 ! unloading & loading again iteration ===> 549 Unload : DO WHILE( jramd == 1) 550 Solver%stiff = 0.D0 551 Solver%load = Element%load 552 CALL formStiff(Node,Element,Material,Spring,Solver) 553 CALL setBoundary(Element,Boundary,Solver) 554 CALL Solve(Solver%no,Solver%width,Solver%stiff,Solver%load,error) 555 CALL setDisplacement(Element,Boundary,Solver) 556 IF(.not. MechanismCheck(Element,File,error)) RETURN 557 CALL SpringStress(Node,Element,Material,Spring,jramc,jramd) 558 IF(jramd == 1) CYCLE Unload 559 CALL incRatio(Element,Material,Spring,Nonlinear) 560 CALL totalValue(Element,Spring,Nonlinear) 561 CALL YieldCheck(Element,Material,Spring) 562 CALL OUTPUT(iste,Element,Spring,Nonlinear,File) 563 END DO Unload 564 IF(NonLinear%rmin > 0.998D0) EXIT 565 IF(iste == NonLinear%iteration) EXIT 566 END DO Iteration 567 END SUBROUTINE Analysis
5-2 ばね係数の作成
RBSM独自の表現方法としてばね定数がある.本プログラムでは,ね定数をばね定数は,ばね毎に計算され,643 D = 0.D0 644 h = Spring%hline(1,is) + Spring%hline(2,is) 645 ie1 = Spring%element(1,is) 646 ie2 = Spring%element(2,is) 647 im1 = Element%material(ie1) 648 im2 = Element%material(ie2) 649 E = (Material%young(im1)*Spring%hline(1,is) & 650 + Material%young(im2)*Spring%hline(2,is))/h 651 P = (Material%poisson(im1)*Spring%hline(1,is) & 652 + Material%poisson(im2)*Spring%hline(2,is))/h 653 IF(Element%type == 0) THEN 654 D(1,1) = E*(1.0-P)/(1.0+P)/(1.0-2.0*P) 655 ELSE 656 D(1,1) = E/(1.0-P**2) 657 END IF 658 D(2,2) = E/(1.0+P)
\[ \left. \begin{array}{rl} k_n & \displaystyle \!\!\!\!\! = \frac{(1-\nu)E}{(1-2 \nu)(1+\nu)} \cdot \frac{1}{h_1+h_2} \\[1em] k_s & \displaystyle \!\!\!\!\! = \frac{E}{1+\nu} \cdot \frac{1}{h_1+h_2} \end{array} \right\} \]
\[ \left. \begin{array}{rl} k_n & \displaystyle \!\!\!\!\! = \frac{E}{(1- \nu^2)} \cdot \frac{1}{h_1+h_2} \\[1em] k_s & \displaystyle \!\!\!\!\! = \frac{E}{1+\nu} \cdot \frac{1}{h_1+h_2} \\[1em] \end{array} \right\} \] ここで,$h_1,h_2$ はばねに関係する各要素の垂線である.プログラムの654行~658行がばね定数を計算している箇所である.プログラムを見ると,式とは異なっていることに気づかれたであろう.式では $h=h_1+h_2$ による除算が行われている,プログラムにはそれが組み込まれていない.これは,後で応力を求めたりするときにこの関係を利用するため,便宣上この段階では $h=h_1+h_2$ で除していないためである.
本サンプル・プログラムでは
5-3 構成行列の作成
前節で弾性状態のばね構成行列 $\boldsymbol{D}$ を計算したが, $\boldsymbol{D}$ 行列は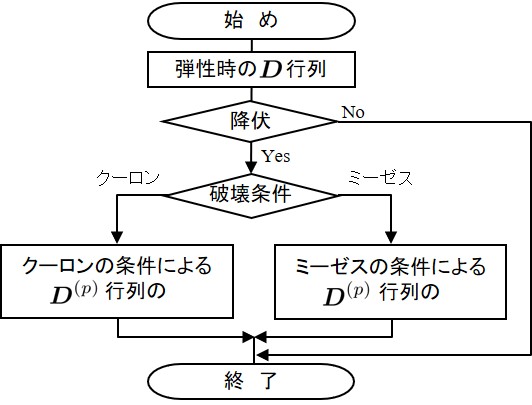
ここで,631 !------------------------------------------------------------------------------- 632 SUBROUTINE formSpring( is, Element, Material, Spring, D ) 633 634 INTEGER, INTENT(IN) :: is 635 TYPE(typeElement), INTENT(IN) :: Element 636 TYPE(typeMaterial), INTENT(IN) :: Material 637 TYPE(typeSpring), INTENT(IN) :: Spring 638 REAL(8), INTENT(INOUT) :: D(:,:) 639 640 REAL(8) :: Dp(2,2),E,P,phi,h 641 INTEGER :: ie1,ie2,im1,im2 642 : : (弾性状態の構成行列D : プログラム5.2参照) : 659 660 IF(Spring%flag(is) == 1) THEN 661 IF(Element%type == 0) THEN 662 phi = (Material%phi(im1)*Spring%hline(1,is) & 663 + Material%phi(im2)*Spring%hline(2,is))/h 664 CALL MohrCoulomb(is,phi,Spring,D,Dp) 665 ELSE 666 CALL vonMises(is,Spring,D,Dp) 667 END IF 668 D = D - Dp 669 END IF 670 END SUBROUTINE formSpring
もし,本書で取り扱つているクーロンの条件やミーゼスの条件以外の破壊条件を利用したい場合はこの
に,それぞれの破壊条件に対する $\boldsymbol{D}^{(p)}$ 行列の作成プログラムを
691行ではせん断力に関する表面力の符号をチェックしている.これは,671 !------------------------------------------------------------------------------- 672 SUBROUTINE MohrCoulomb( is, phi, Spring, D, Dp ) 673 674 INTEGER, INTENT(IN) :: is 675 REAL(8), INTENT(IN) :: phi 676 TYPE(typeSpring), INTENT(IN) :: Spring 677 REAL(8), INTENT(IN) :: D(:,:) 678 REAL(8), INTENT(OUT) :: Dp(:,:) 679 680 REAL(8) :: pt,f,D1,D2 681 INTEGER :: i,j 682 REAL(8) :: PAI = 3.141592654D0 683 684 pt = DTAN(phi*PAI/180.D0) 685 D1 = D(1,1) 686 D2 = D(2,2) 687 f = 1.D0/(D2+D1*pt**2) 688 Dp(1,1) = (D1*pt)**2*f 689 Dp(2,2) = D2*D2*f 690 Dp(1,2) = D1*D2*pt*f 691 IF(Spring%stress(2,is) < 0.D0) THEN 692 Dp(1,2) = -Dp(1,2) 693 END IF 694 Dp(2,1) = Dp(1,2) 695 END SUBROUTINE MohrCoulomb
696 !------------------------------------------------------------------------------- 697 SUBROUTINE vonMises( is, Spring, D, Dp ) 698 699 INTEGER, INTENT(IN) :: is 700 TYPE(typeSpring), INTENT(IN) :: Spring 701 REAL(8), INTENT(IN) :: D(:,:) 702 REAL(8), INTENT(OUT) :: Dp(:,:) 703 704 REAL(8) :: sig,tau,f,D1,D2 705 INTEGER :: i,j 706 707 D1 = D(1,1) 708 D2 = D(2,2) 709 sig = Spring%stress(1,is) 710 tau = Spring%Stress(2,is) 711 f = 1.D0/(D1*sig*sig/4.D0 + 4.D0*D2*tau*tau) 712 Dp(1,1) = D1*D1*sig*sig/4.D0*f 713 Dp(2,2) = 4.D0*D2*D2*tau*tau*f 714 Dp(1,2) = D1*D2*sig*tau*f 715 Dp(2,1) = Dp(1,2) 716 END SUBROUTINE vonMises
5-4 ばね剛性行列の作成
RBSMの場合,弾性時は構成行列の非対角項が0であり,塑性化後には非対角項が非零となるのが一般的である.前者の弾性状態に対して積分を実行した結果得られたばね剛性行列が
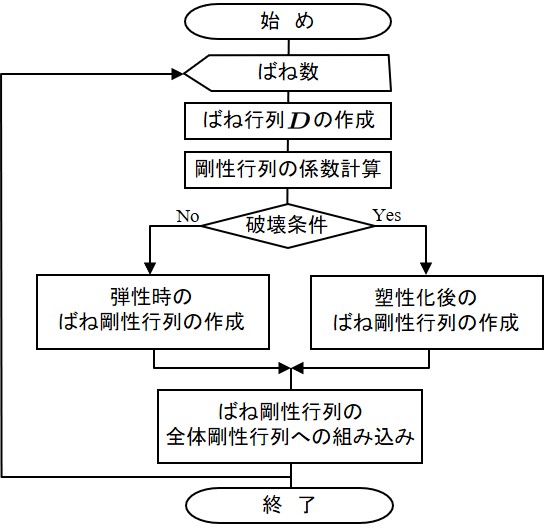
本サブルーチン内において呼び出されるサブルーチンのうち,621行目の608 !------------------------------------------------------------------------------- 609 SUBROUTINE formStiff( Node, Element, Material, Spring, Solver) 610 611 TYPE(typeNode), INTENT(IN) :: Node 612 TYPE(typeElement), INTENT(IN) :: Element 613 TYPE(typeMaterial), INTENT(IN) :: Material 614 TYPE(typeSpring), INTENT(IN) :: Spring 615 TYPE(typeBand), INTENT(INOUT) :: Solver 616 617 REAL(8) :: sfm(6,6),coef(6),D(2,2) 618 INTEGER :: is 619 620 DO is = 1, Spring%no 621 CALL formSpring(is,Element,Material,Spring,D) 622 CALL coefStiff(is,Node,Spring,coef) 623 IF(Spring%flag(is) /= 1) THEN 624 CALL elasticStiff(is,Element,Material,Spring,D,coef,sfm) 625 ELSE 626 CALL plasticStiff(is,Element,Material,Spring,D,coef,sfm) 627 END IF 628 CALL Assemble(is,sfm,Spring,Solver) 629 END DO 630 END SUBROUTINE formStiff
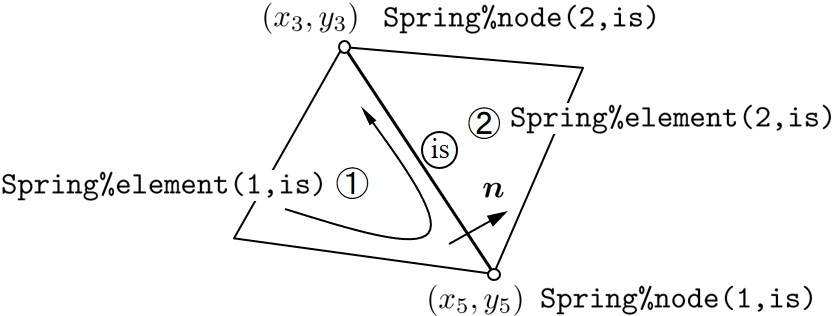
ばね剛性行列を作成するため予め行う係数の計算は
717 !------------------------------------------------------------------------------- 718 SUBROUTINE coefStiff( is, Node, Spring, coef ) 719 720 INTEGER, INTENT(IN) :: is 721 TYPE(typeNode), INTENT(IN) :: Node 722 TYPE(typeSpring), INTENT(IN) :: Spring 723 REAL(8), INTENT(OUT) :: coef(:) 724 725 INTEGER :: ie1,ie2,in1,in2 726 REAL(8) :: x31,x32,x51,x52,y31,y32,y51,y52 727 728 ie1 = Spring%element(1,is) 729 ie2 = Spring%element(2,is) 730 in1 = Spring%node(1,is) 731 in2 = Spring%node(2,is) 732 x31 = Node%coord(1,in2) - Element%center(1,ie1) 733 x32 = Node%coord(1,in2) - Element%center(1,ie2) 734 x51 = Node%coord(1,in1) - Element%center(1,ie1) 735 x52 = Node%coord(1,in1) - Element%center(1,ie2) 736 y31 = Node%coord(2,in2) - Element%center(2,ie1) 737 y32 = Node%coord(2,in2) - Element%center(2,ie2) 738 y51 = Node%coord(2,in1) - Element%center(2,ie1) 739 y52 = Node%coord(2,in1) - Element%center(2,ie2) 740 coef(1) = Node%coord(1,in2) - Node%coord(1,in1) 741 coef(2) = Node%coord(2,in2) - Node%coord(2,in1) 742 coef(3) = 0.5*( coef(1)*(x31+x51) + coef(2)*(y31+y51)) 743 coef(4) = 0.5*( coef(1)*(y32+y52) - coef(2)*(x32+x52)) 744 coef(5) = 0.5*(-coef(1)*(y31+y51) + coef(2)*(x31+x51)) 745 coef(6) = 0.5*(-coef(1)*(x32+x52) - coef(2)*(y32+y52)) 746 END SUBROUTINE coefStiff
769行~771行がばね係数 \[ \left. \begin{array}{l} \displaystyle {\rm Kd} = \frac{k_n}{l} \\ \displaystyle {\rm Ks} = \frac{k_s}{l} \\ \displaystyle {\rm Kr} = \frac{k_n \cdot l^4}{12 l} \end{array} \right\} \] を計算している箇所である.747 !------------------------------------------------------------------------------- 748 SUBROUTINE elasticStiff( is, Element, Material, Spring, D, coef, sfm ) 749 750 INTEGER, INTENT(IN) :: is 751 TYPE(typeElement), INTENT(IN) :: Element 752 TYPE(typeMaterial), INTENT(IN) :: Material 753 TYPE(typeSpring), INTENT(IN) :: Spring 754 REAL(8), INTENT(IN) :: D(:,:) 755 REAL(8), INTENT(IN) :: coef(:) 756 REAL(8), INTENT(OUT) :: sfm(:,:) 757 758 REAL(8) :: h,thick,Kd,Ks,Kr 759 REAL(8) :: x35,y35,D11,D12,D21,D22 760 INTEGER :: ie1,ie2,im1,im2,i,j 761 762 h = Spring%hline(1,is) + Spring%hline(2,is) 763 ie1 = Spring%element(1,is) 764 ie2 = Spring%element(2,is) 765 im1 = Element%material(ie1) 766 im2 = Element%material(ie2) 767 thick = (Material%thick(im1)*Spring%hline(1,is) & 768 + Material%thick(im2)*Spring%hline(2,is))/H 769 Kd = D(1,1)/Spring%length(is)/h*thick 770 Ks = D(2,2)/Spring%length(is)/h*thick 771 Kr = Kd*Spring%length(is)**4/12.D0 772 x35 = coef(1) 773 y35 = coef(2) 774 D11 = coef(3) 775 D12 = coef(4) 776 D21 = coef(5) 777 D22 = coef(6) 778 sfm(1,2) = -(Kd-Ks)*x35*y35 779 sfm(1,3) = Kd*y35*D11 - Ks*x35*D21 780 sfm(1,4) = -(Kd*y35*y35 + Ks*x35*x35) 781 sfm(1,5) = -sfm(1,2) 782 sfm(1,6) = Kd*y35*D22 - Ks*x35*D12 783 sfm(2,3) = -(Kd*x35*D11 + Ks*y35*D21) 784 sfm(2,4) = -sfm(1,2) 785 sfm(2,5) = -(Kd*x35*x35 + Ks*y35*y35) 786 sfm(2,6) = -(Kd*x35*D22 + Ks*y35*D12) 787 sfm(3,4) = -sfm(1,3) 788 sfm(3,5) = -sfm(2,3) 789 sfm(3,6) = Kd*D11*D22 + Ks*D21*D12 - Kr 790 sfm(4,5) = sfm(1,2) 791 sfm(4,6) = -sfm(1,6) 792 sfm(5,6) = -sfm(2,6) 793 DO i = 1, 6 794 DO j = i, 6 795 sfm(j,i) = sfm(i,j) 796 END DO 797 END DO 798 sfm(1,1) = -sfm(1,4) 799 sfm(2,2) = -sfm(2,5) 800 sfm(3,3) = Kd*D11*D11 + Ks*D21*D21 + Kr 801 sfm(4,4) = sfm(1,1) 802 sfm(5,5) = sfm(2,2) 803 sfm(6,6) = Kd*D22*D22 + Ks*D12*D12 + Kr 804 END SUBROUTINE elasticStiff
778行~792行ではばね剛性行列の対角項を除く上半分を計算している.ばね剛性行列は対称行列となるため,下半分は793行~797行に示すよう,入れ替え作業によって設定している.798行~803行は残りの対角項に関する成分を
同様にして,塑性化後のばね剛性行列を作成する
塑性化後,構成行列の非対角項が追加になるため,829行においてその影響(Kds)の設定を行つている.837行~862行において作成している805 !------------------------------------------------------------------------------- 806 SUBROUTINE plasticStiff( is, Element, Material, Spring, D, coef, sfm ) 807 808 INTEGER, INTENT(IN) :: is ! spring number 809 TYPE(typeElement), INTENT(IN) :: Element ! Element Data 810 TYPE(typeMaterial), INTENT(IN) :: Material ! Material Data 811 TYPE(typeSpring), INTENT(IN) :: Spring ! Spring Data 812 REAL(8), INTENT(IN) :: D(:,:) ! Sprin matrix 813 REAL(8), INTENT(IN) :: coef(:) ! coefficient of spring stiffness 814 REAL(8), INTENT(OUT) :: sfm(:,:) ! spring matrix 815 816 REAL(8) :: h,thick,Kd,Ks,Kds,Kr 817 REAL(8) :: x35,y35,D11,D12,D21,D22 818 INTEGER :: ie1,ie2,im1,im2,i,j 819 820 h = Spring%hline(1,is) + Spring%hline(2,is) 821 ie1 = Spring%element(1,is) 822 ie2 = Spring%element(2,is) 823 im1 = Element%material(ie1) 824 im2 = Element%material(ie2) 825 thick = (Material%thick(im1)*Spring%hline(1,is) & 826 + Material%thick(im2)*Spring%hline(2,is))/H 827 Kd = D(1,1)/Spring%length(is)/h*thick 828 Ks = D(2,2)/Spring%length(is)/h*thick 829 Kds = D(1,2)/Spring%length(is)/h*thick 830 Kr = Kd*Spring%length(is)**4/12.D0 831 x35 = coef(1) 832 y35 = coef(2) 833 D11 = coef(3) 834 D12 = coef(4) 835 D21 = coef(5) 836 D22 = coef(6) 837 sfm(1,2) = -(Kd-Ks)*x35*y35 + (y35*y35-x35*x35)*Kds 838 sfm(1,3) = Kd*y35*D11 - Ks*x35*D21 + (x35*D11-y35*D21)*Kds 839 sfm(1,4) = -(Kd*y35*y35 + Ks*x35*x35) -2.0*x35*y35*Kds 840 sfm(1,5) = -sfm(1,2) 841 sfm(1,6) = Kd*y35*D22 - Ks*x35*D12 + (x35*D22-y35*D12)*Kds 842 sfm(2,3) = -(Kd*x35*D11 + Ks*y35*D21) + (x35*D21+y35*D11)*Kds 843 sfm(2,4) = -sfm(1,2) 844 sfm(2,5) = -(Kd*x35*x35 + Ks*y35*y35) + 2.0*x35*y35*Kds 845 sfm(2,6) = -(Kd*x35*D22 + Ks*Y35*D12) + (x35*D12+y35*D22)*Kds 846 sfm(3,4) = -sfm(1,3) 847 sfm(3,5) = -sfm(2,3) 848 sfm(3,6) = Kd*D11*D22 + Ks*D21*D12 - Kr - (D11*D12 + D21*D22)*Kds 849 sfm(4,5) = sfm(1,2) 850 sfm(4,6) = -sfm(1,6) 851 sfm(5,6) = -sfm(2,6) 852 DO i = 1, 6 853 DO j = i, 6 854 sfm(j,i) = sfm(i,j) 855 END DO 856 END DO 857 sfm(1,1) = -sfm(1,4) 858 sfm(2,2) = -sfm(2,5) 859 sfm(3,3) = Kd*D11*D11 + Ks*D21*D21 + Kr - 2.D0*D11*D21*Kds 860 sfm(4,4) = sfm(1,1) 861 sfm(5,5) = sfm(2,2) 862 sfm(6,6) = Kd*D22*D22 + Ks*D12*D12 + Kr - 2.D0*D22*D12*Kds 863 END SUBROUTINE plasticStiff
5-5 全体剛性行列の作成
本サンプル・プログラムでは全体剛性行列をバンド法により解いている.メモリーを効率よく利用するためには全体剛性行列を1次元配列にするとよく,このような方法はFEMにおいても頻繁に行われている.RBSMの場合,ばね剛性行列を全体剛性行列に組み込むことになるが,組み込み方法もFEMにおける節点及び要素を,それぞれ,RBSMの要素とばねに対応させれば,FEMの場合と全く同様である.詳細については他の書物にゆずるとし,ここではどのように全体剛性行列を1次元配列にセットするかについて説明する.さて,全体剛性行列をバンド化すると
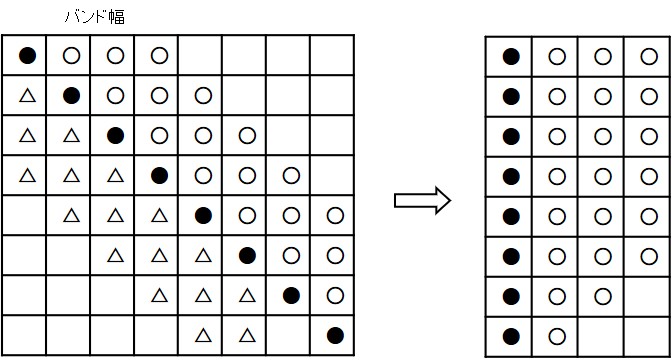
$\hspace{7em}$

以上の考えをもとにプログラム化したものが,
本サプルーチンはバンド法のための全体剛性行列を作成するものであり,連立方程式の解析法を,例えばスカイライン法などに変更する場合には本サブルーチンもそれに対応するよう取り替える必要がある.864 !------------------------------------------------------------------------------- 865 SUBROUTINE Assemble( is, sfm, Spring, Solver) 866 867 INTEGER, INTENT(IN) :: is 868 REAL(8), INTENT(IN) :: sfm(:,:) 869 TYPE(typeSpring), INTENT(IN) :: Spring 870 TYPE(typeBand), INTENT(INOUT) :: Solver 871 872 INTEGER :: ie1,ie2,i,j,k,l,k1,ka,kb,la,lb 873 874 DO i = 1, 2 875 ie1 = Spring%element(i,is) 876 DO j = i, 2 877 ie2 = Spring%element(j,is) 878 DO k = 1, 3 879 k1 = k 880 IF(i /= j) THEN 881 k1 = 1 882 END IF 883 DO l = k1, 3 884 ka = k + (i-1)*3 885 kb = l + (j-1)*3 886 la = k + (ie1-1)*3 887 lb = l + (ie2-1)*3 888 IF(lb < la) THEN 889 kb = k + (i-1)*3 890 ka = l + (j-1)*3 891 lb = k + (ie1-1)*3 892 la = l + (ie2-1)*3 893 END IF 894 lb = lb + (la-1)*Solver%width - la + 1 895 Solver%stiff(lb) = Solver%stiff(lb) + sfm(ka,kb) 896 END DO 897 END DO 898 END DO 899 END DO 900 END SUBROUTINE Assemble
5-6 表面力の計算
変位型のFEMでは,テンソル量としての要素内応力を求める.一方,RBSMでは隣接する2要素間の境界辺上における単位面積当りの表面力を求める.両者の間にこのような相違はあるものの,計算に関する全体のプログラムの流れにはあまり差がない.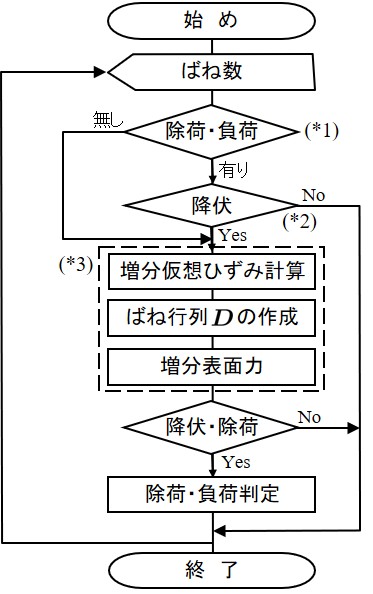
本来の表面力計算に関する部分は(*3)に示す,点線で囲まれた部分であるが,図を見ると単純に表面力を計算する部分のみならず,除荷や負荷の判定が含まれている.このように,山田の方法を用いて非線形計算を行う場合には除荷や負荷の判定を行つておく必要がある.
プログラムを簡単にし,理解しやすいようにするなら,(*3)に示す部分を取り出し,増分表面力計算の部分と除荷,負荷の部分を別なサブルーチンにより処理した方がよいが,ここでは,計算の効率化を考え,同一サブルーチン内で処理している.これは,除荷や負荷が生じた場合,今回の荷重増分計算を無効とし,剛性を変えて再計算するためである.本サンプル・プログラムでは前回のばね状態が降伏状態で今回の増分計算により除荷が発生したならば,剛性を弾性状態に変えて再計算を行つている.また,除荷状態から負荷状態に変われば剛性を降伏状態に変えて再計算を行う.本書では簡単な降伏条件を用いているが,さらに複雜な降伏条件を用いるなら,当然この判定や剛性の考え方は変わってくる.除荷,負荷については次節にゆずるとし,ここでは,おおまかな計算の流れをもう少し考えてみよう.
(*1)に示す判定文では増分計算あるいは再計算過程において除荷あるいは負荷が発生したばねが存在するか否かのチェックを行つている.もし,一箇所以上のばねに除荷もしくは負荷が発生していたなら,以後,降伏しているばねについてのみ $\lambda$ 計算のための増分計算をおこない,再計算を行う準備を行う.この降伏の判定文が(*2)である.除荷,負荷が発生していなければ通常の(*3)に示す増分計算を行う.
この計算の流れをプログラム化したものが
974 !------------------------------------------------------------------------------- 975 SUBROUTINE SpringStress( Node, Element, Material, Spring, jramc, jramd ) 976 977 TYPE(typeNode), INTENT(IN) :: Node 978 TYPE(typeElement), INTENT(IN) :: Element 979 TYPE(typeMaterial), INTENT(IN) :: Material 980 TYPE(typeSpring), INTENT(INOUT) :: Spring 981 INTEGER, INTENT(INOUT) :: jramc 982 INTEGER, INTENT(INOUT) :: jramd 983 984 REAL(8) :: D(2,2),ww 985 INTEGER :: is,jbit,i,j 986 987 jramd = 0 988 DO is = 1, Spring%no 989 IF(jramd == 1 .AND. Spring%flag(is) == 0) CYCLE 990 IF(jramd == 1 .AND. Spring%flag(is) == -2) CYCLE 991 CALL Strain(is,Node,Element,Spring) 992 CALL formSpring(is,Element,Material,Spring,D) 993 DO i = 1, 2 994 ww = 0.0 995 DO j = 1, 2 996 ww = ww + D(i,j)*Spring%dstrain(j,is) 997 END DO 998 Spring%dstress(i,is) = ww 999 END DO 1000 IF(jramc < 2) THEN 1001 IF(Spring%flag(is) == 1 .OR. Spring%flag(is) == 2) THEN 1002 jbit = 0 1003 IF(Spring%flag(is) == 2) jbit = 1 1004 CALL Unload(is,Element,Material,Spring,D,jramd,jbit) 1005 END IF 1006 END IF 1007 END DO 1008 jramc = jramc + 1 1009 END SUBROUTINE SpringStress
また,1002行に示す
1000行及び1008行に示す
次ぎに,
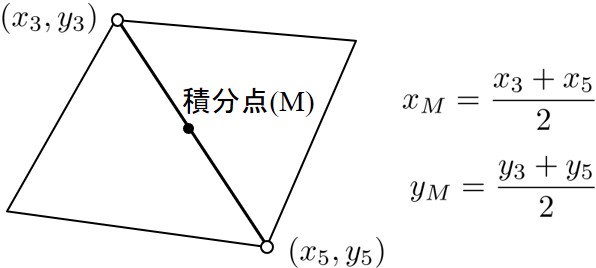
この結果,仮想ひずみ増分は1040 !------------------------------------------------------------------------------- 1041 SUBROUTINE Bmatrix( is, Node, Element, Spring, BB ) 1042 1043 INTEGER, INTENT(IN) :: is 1044 TYPE(typeNode), INTENT(IN) :: Node 1045 TYPE(typeElement), INTENT(IN) :: Element 1046 TYPE(typeSpring), INTENT(IN) :: Spring 1047 REAL(8), INTENT(OUT) :: BB(:,:) 1048 1049 REAL(8) :: yl1,yl2,ym1,ym2,x,y 1050 INTEGER :: in1,in2,ie1,ie2 1051 1052 in1 = Spring%node(1,is) 1053 in2 = Spring%node(2,is) 1054 ie1 = Spring%element(1,is) 1055 ie2 = Spring%element(2,is) 1056 yl1 = (Node%coord(2,in2)-Node%coord(2,in1))/Spring%length(is) 1057 yl2 = (Node%coord(1,in2)-Node%coord(1,in1))/Spring%length(is) 1058 ym1 =-yl2 1059 ym2 = yl1 1060 x = (Node%coord(1,in1)+Node%coord(1,in2))/2.D0 1061 y = (Node%coord(2,in1)+Node%coord(2,in2))/2.D0 1062 BB(1,1) = -yl1 1063 BB(1,2) = -ym1 1064 BB(1,3) = -yl1*(y-Element%center(2,ie1)) + ym1*(x-Element%center(1,ie1)) 1065 BB(1,4) = -BB(1,1) 1066 BB(1,5) = -BB(1,2) 1067 BB(1,6) = yl1*(y-Element%center(2,ie2)) - ym1*(x-Element%center(1,ie2)) 1068 BB(2,1) = -yl2 1069 BB(2,2) = -ym2 1070 BB(2,3) = -yl2*(y-Element%center(2,ie1)) + ym2*(x-Element%center(1,ie1)) 1071 BB(2,4) = -BB(2,1) 1072 BB(2,5) = -BB(2,2) 1073 BB(2,6) = yl2*(y-Element%center(2,ie2)) - ym2*(x-Element%center(1,ie2)) 1074 END SUBROUTINE Bmatrix
仮想ひずみ増分が計算できれば,表面力が以下のように計算できる. \[ \boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\varepsilon} \] この計算は1010 !------------------------------------------------------------------------------- 1011 SUBROUTINE Strain( is, Node, Element, Spring ) 1012 1013 INTEGER, INTENT(IN) :: is 1014 TYPE(typeNode), INTENT(IN) :: Node 1015 TYPE(typeElement), INTENT(IN) :: Element 1016 TYPE(typeSpring), INTENT(INOUT) :: Spring 1017 1018 REAL(8) :: uu(2*Element%dof),BB(2,2*Element%dof),h,ww 1019 INTEGER :: ie,i,j,ii,jj 1020 1021 ii = 0 1022 DO i = 1, 2 1023 ie = Spring%element(i,is) 1024 DO j = 1, 3 1025 ii = ii + 1 1026 jj = j + (ie-1)*Element%dof 1027 uu(ii) = Element%ddisp(jj) 1028 END DO 1029 END DO 1030 CALL Bmatrix(is,Node,Element,Spring,BB) 1031 h = Spring%hline(1,is) + Spring%hline(2,is) 1032 DO i = 1, 2 1033 ww = 0.D0 1034 DO j = 1, 2*Element%dof 1035 ww = ww + BB(i,j)*uu(j) 1036 END DO 1037 Spring%dstrain(i,is) = ww/h 1038 END DO 1039 END SUBROUTINE Strain
要素内応力と隣接する2要素間の表面力という差はあるが,基本的にはFEMの計算過程と同じであることに気づかれたであろう.この後,FEMでは主応力の計算を行うが,RBSMではベクトルとしての表面力をそのまま取り扱うため,主応力のような計算はない.
5-7 除荷・負荷の判定
前節で,単位面積当りの表面力を計算する過程において,除荷,負荷の判定が必要であることを述べた.本節ではこのことについて説明する.完全弾塑性体を考えた場合,除荷は
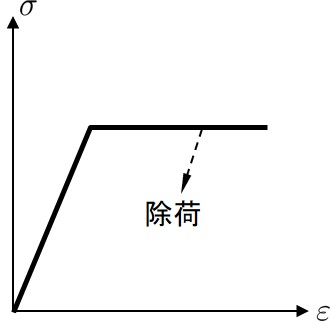
$\hspace{4em}$
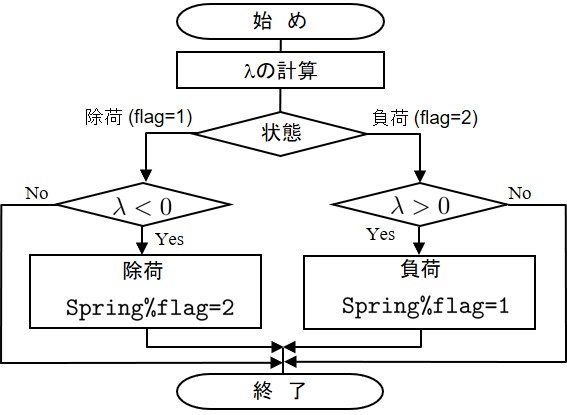
除荷状態 → $\lambda > 0$ → 負荷発生 → Spring%flag = 1 以上の判定をプログラム化したものが
1075 !------------------------------------------------------------------------------- 1076 SUBROUTINE Unload( is, Element, Material, Spring, D, jramd, jbit) 1077 1078 INTEGER, INTENT(IN) :: is 1079 TYPE(typeElement), INTENT(IN) :: Element 1080 TYPE(typeMaterial), INTENT(IN) :: Material 1081 TYPE(typeSpring), INTENT(INOUT) :: Spring 1082 REAL(8), INTENT(IN) :: D(:,:) 1083 INTEGER, INTENT(INOUT) :: jramd 1084 INTEGER, INTENT(IN) :: jbit 1085 1086 REAL(8) :: lam ! lambda 1087 1088 lam = Lambda(is,Element,Material,Spring,D) 1089 IF(jbit /= 1) THEN 1090 IF(lam < 0.D0) THEN 1091 Spring%flag(is) = 2 1092 jramd = 1 1093 END IF 1094 ELSE 1095 IF(lam > 0.D0) THEN 1096 Spring%flag(is) = 1 1097 jramd = 1 1098 END IF 1099 END IF 1100 END SUBROUTINE Unload
このサブルーチンに現れる $\lambda$ の計算は
クーロンの条件の場合,$\lambda$ の計算式に強度定数が含まれている.本書のサンプル・プログラムでは,この強度定数に対しても垂線を重みとして平均値をとるよう考えている.この平均値の計算は1101 !------------------------------------------------------------------------------- 1102 FUNCTION Lambda( is, Element, Material, Spring, D ) RESULT( lam ) 1103 1104 INTEGER, INTENT(IN) :: is 1105 TYPE(typeElement), INTENT(IN) :: Element 1106 TYPE(typeMaterial), INTENT(IN) :: Material 1107 TYPE(typeSpring), INTENT(IN) :: Spring 1108 REAL(8), INTENT(IN) :: D(:,:) 1109 REAL(8) :: lam 1110 1111 REAL(8) :: cm,phi,pt 1112 REAL(8) :: PAI = 3.141592654D0 1113 1114 lam = 0.0 1115 IF(Element%type == 0) THEN 1116 CALL strength(is,Element,Material,Spring,cm,phi) 1117 pt = DTAN(phi*PAI/180.D0) 1118 lam = D(2,2)*Spring%stress(2,is)*Spring%dstrain(2,is) & 1119 + D(1,1)*(cm-Spring%stress(1,is)*pt)*pt*Spring%dstrain(1,is) 1120 ELSE 1121 lam = 2.0*D(2,2)*Spring%stress(2,is)*Spring%dstrain(2,is) & 1122 + 0.5*D(1,1)*Spring%stress(1,is)*Spring%dstrain(1,is) 1123 END IF 1124 END FUNCTION Lambda
1143,1144行における1125 !------------------------------------------------------------------------------- 1126 SUBROUTINE strength( is, Element, Material, Spring, cm, phi ) 1127 1128 INTEGER, INTENT(IN) :: is 1129 TYPE(typeElement), INTENT(IN) :: Element 1130 TYPE(typeMaterial), INTENT(IN) :: Material 1131 TYPE(typeSpring), INTENT(IN) :: Spring 1132 REAL(8), INTENT(OUT) :: cm 1133 REAL(8), INTENT(OUT) :: phi 1134 1135 REAL(8) :: h 1136 INTEGER :: ie1,ie2,im1,im2 1137 1138 h = Spring%hline(1,is) + Spring%hline(2,is) 1139 ie1 = Spring%element(1,is) 1140 ie2 = Spring%element(2,is) 1141 im1 = Element%material(ie1) 1142 im2 = Element%material(ie2) 1143 cm = (Material%c(im1)*Spring%hline(1,is) & 1144 + Material%c(im2)*Spring%hline(2,is))/h 1145 phi = (Material%phi(im1)*Spring%hline(1,is) & 1146 + Material%phi(im2)*Spring%hline(2,is))/h 1147 END SUBROUTINE strength
なお,本サンプル・プログラムでは除荷時の再計算におけるばね剛性行列に弾性剛性を,また,負荷時の剛性行列には塑性化後の剛性を用いている.
5-8 荷重増分率の計算
山田の方法により増分計算を行う場合,荷重増分率はプログラム内部で自動的に計算される.本節では,このことについて若干の補足をしょう.塑性流れ則に従えば,すでに降伏しているばね表面力は,除荷が発生しない限り
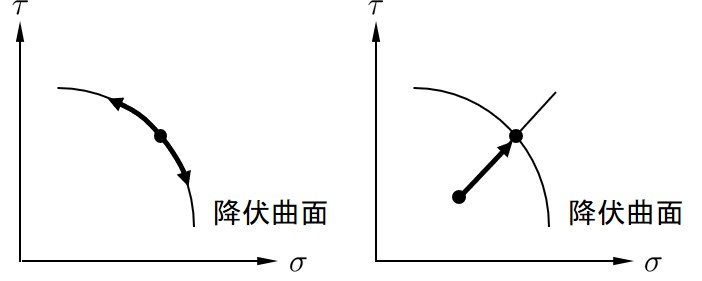
$\hspace{7em}$
これらの関係をプログラム化したものが
2次方程式の根は1148 !------------------------------------------------------------------------------- 1149 SUBROUTINE incRatio( Element, Material, Spring, Nonlinear ) 1150 1151 TYPE(typeElement), INTENT(IN) :: Element 1152 TYPE(typeMaterial), INTENT(IN) :: Material 1153 TYPE(typeSpring), INTENT(IN) :: Spring 1154 TYPE(typeNonLinear),INTENT(INOUT) :: NonLinear 1155 1156 REAL(8) :: minStep,step,cm,phi,pt,a,b,c 1157 INTEGER :: is 1158 REAL(8) :: PAI = 3.141592654D0 1159 1160 minStep = 9999.D0 1161 DO is = 1, Spring%no 1162 CALL strength(is,Element,Material,Spring,cm,phi) 1163 IF(Element%type == 0) THEN 1164 pt = DTAN(phi*PAI/180.D0) 1165 a = Spring%dstress(2,is)**2 - (Spring%dstress(1,is)*pt)**2 1166 b = 2.D0*(Spring%stress(2,is)*Spring%dstress(2,is) & 1167 + (cm-Spring%stress(1,is)*pt)*Spring%dstress(1,is)*pt) 1168 c = Spring%stress(2,is)**2 - (cm-Spring%stress(1,is)*pt)**2 1169 ELSE 1170 a = (Spring%dstress(1,is)**2)/4.D0 + Spring%dstress(2,is)**2 1171 b = Spring%stress(1,is)*Spring%dstress(1,is)/2.D0 & 1172 + 2.D0*Spring%stress(2,is)*Spring%dstress(2,is) 1173 c = (Spring%stress(1,is)**2)/4.D0 + Spring%stress(2,is)**2 & 1174 - cm**2 1175 END IF 1176 step = ratio(a,b,c) 1177 IF(minStep > step) THEN 1178 minStep = step 1179 END IF 1180 END DO 1181 NonLinear%step = minStep 1182 NonLinear%rmin = NonLinear%rmin + minStep 1183 IF(NonLinear%rmin > 0.9998D0) THEN 1184 NonLinear%step = NonLinear%step - NonLinear%rmin + 1.D0 1185 NonLinear%rmin = 1.D0 1186 END IF 1187 END SUBROUTINE incRatio
数値計算では丸め誤差など,各種の誤差が混入するため,厳密に荷重増分率の累計が1.0となることはまれである.そこで1183行に示すよう,倍精度計算の場合NonLinear%rminが0.9998以上であればほぼ100%の荷重が作用したものとみなし,1185行のように強制的にNonLinear%rminを1にセットする.このとき,最後の
以上のようにして荷重増分率が決定されたなら,今回までの全変位及び全表面力が以下のように求められる. \[ \left. \begin{array}{l} \boldsymbol{u}^{n+1} = \boldsymbol{u}^{n} + \Delta \boldsymbol{u}^{n+1} \cdot {\rm step} \\ \boldsymbol{\sigma}^{n+1} = \boldsymbol{\sigma}^{n} + \Delta \boldsymbol{\sigma}^{n+1} \cdot {\rm step} \\ \boldsymbol{\varepsilon}^{n+1} = \boldsymbol{\varepsilon}^{n} + \Delta \boldsymbol{\varepsilon}^{n+1} \cdot {\rm step} \end{array} \right\} \] ここで上付きの(n)が前回までの全変位及び全表面力で(n+1)が今回の量であることを示す.1188 !------------------------------------------------------------------------------- 1189 FUNCTION ratio( a, b, c ) RESULT( step ) 1190 1191 REAL(8), INTENT(IN) :: a,b,c 1192 REAL(8) :: step 1193 1194 REAL(8) :: r1,r2,b1 1195 REAL(8) :: eps = 1.0D-8 1196 1197 step = 9999.D0 1198 IF(DABS(a) <= eps) THEN 1199 IF(DABS(b)>= eps) THEN 1200 r2 = -c/b 1201 IF(r2 >0.D0) THEN 1202 step = r2 1203 END IF 1204 END IF 1205 ELSE 1206 b1 = b**2 - 4.D0*a*c 1207 IF(b1 >= eps) THEN 1208 r1 = (-b+DSQRT(b1))/(2.D0*a) 1209 r2 = (-b-DSQRT(b1))/(2.D0*a) 1210 IF(r1 < 0.D0) THEN 1211 IF(r2 > 0.D0) THEN 1212 step = r2 1213 END IF 1214 ELSE 1215 IF(r2 < 0.D0) THEN 1216 step = r1 1217 ELSE 1218 IF(r1 < r2) THEN 1219 step = r1 1220 ELSE 1221 step = r2 1222 END IF 1223 END IF 1224 END IF 1225 END IF 1226 END IF 1227 END FUNCTION ratio
この関係をもとにプログラム化したものが
1228 !------------------------------------------------------------------------------- 1229 SUBROUTINE totalValue( Element, Spring, Nonlinear ) 1230 1231 TYPE(typeElement), INTENT(INOUT) :: Element 1232 TYPE(typeSpring), INTENT(INOUT) :: Spring 1233 TYPE(typeNonLinear),INTENT(IN) :: NonLinear 1234 1235 Element%disp = Element%disp + Element%ddisp*NonLinear%step 1236 Spring%strain = Spring%strain + Spring%dstrain*NonLinear%step 1237 Spring%stress = Spring%stress + Spring%dstress*NonLinear%step 1238 END SUBROUTINE totalValue
5-9 破壊判定
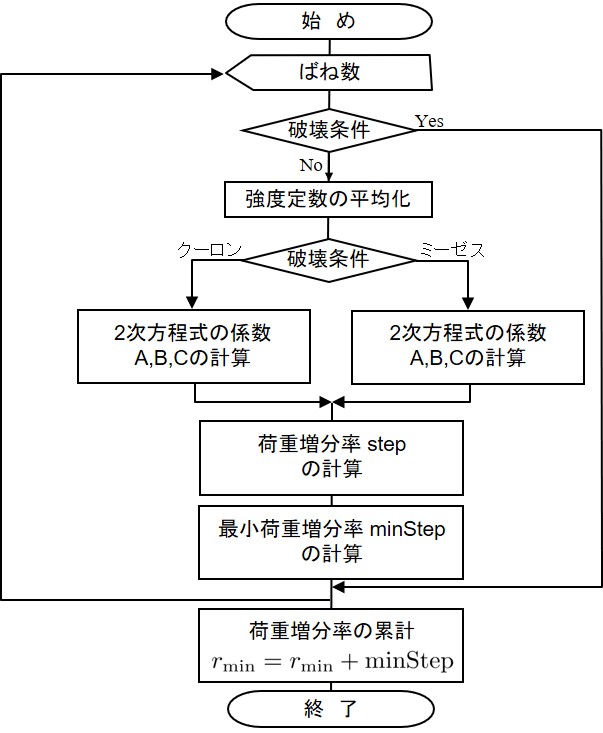
山田の方法を用いた荷重増分計算では増分計算毎に塑性化したばねの剛性行列を作成し直す.このためには,前回のばね状態が弾性状態か塑性状態か,あるいは除荷状態か負荷状態かを把握しておく必要がある.この判定の流れを示したものが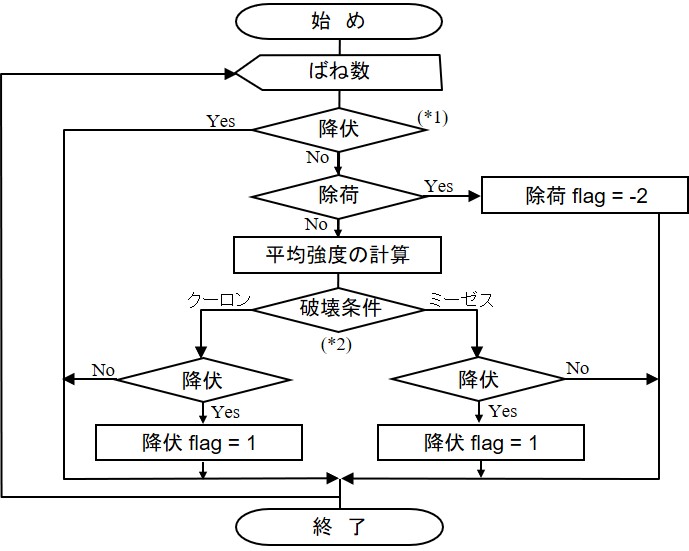
Spring%flag = 1 : 降伏状態
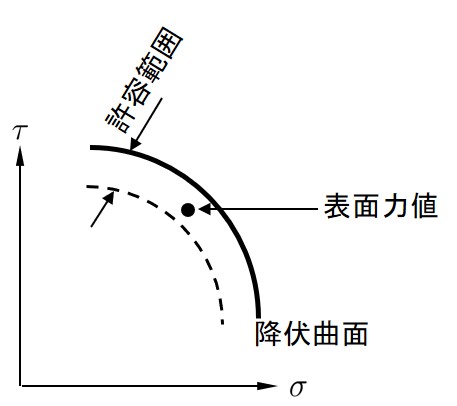
Spring%flag = -2 : 除荷状態 図に示す(*1)の判定は,すでに降伏状態にあるばねか否かを判定している.降伏状態にあれば除荷が発生しない限り塑性状態を継続するものとしてフラッグの変更を行わない.もし,ばねが降伏状態でなければ除荷状態か否かを判定し,除荷状態であるば以後弾性と見なし,フラッグをSpring%flag = -2にセットする.(*2)の判定文は今回の表面力が降伏しているか否かの判定で,もし,降伏していればフラッグを1とし,以後,塑性としての取り扱いをする.このフローをプログラム化したものが
この判定で注意してほしいことは1257行と1264行においてせん断強さに0.998を掛けていることである.厳密にはこのようなことを行う必要はないが,実数計算の場合,丸め誤差等により本来1となるべき解が0.99…となってしまうことが度々ある.前節で説明した全表面力の計算も実数計算であるから,表面力が降伏曲面上に完全に一致することは少ない.1239 !------------------------------------------------------------------------------- 1240 SUBROUTINE YieldCheck( Element, Material, Spring ) 1241 1242 TYPE(typeElement), INTENT(IN) :: Element ! Element Data 1243 TYPE(typeMaterial), INTENT(IN) :: Material ! Material Data 1244 TYPE(typeSpring), INTENT(IN) :: Spring ! Spring Data 1245 1246 INTEGER :: is 1247 REAL(8) :: cm,phi,pt,tau 1248 REAL(8) :: PAI = 3.141592654D0 1249 1250 DO is = 1, Spring%no 1251 IF(Spring%flag(is) /= 1) THEN 1252 IF(Spring%flag(is) ==2) THEN 1253 Spring%flag(is) = -2 1254 ELSE 1255 CALL strength(is,Element,Material,Spring,cm,phi) 1256 IF(Element%type == 0) THEN 1257 cm = cm*0.998D0 1258 pt = DTAN(phi*PAI/180.0) 1259 tau = ABS(Spring%stress(2,is))+Spring%stress(1,is)*pt 1260 IF(tau > cm) THEN 1261 Spring%flag(is) = 1 1262 END IF 1263 ELSE 1264 cm = cm**2*0.998D0 1265 tau = Spring%stress(1,is)**2/4.D0 + Spring%stress(2,is)**2 1266 IF(tau > cm) THEN 1267 Spring%flag(is) = 1 1268 END IF 1269 END IF 1270 END IF 1271 END IF 1272 END DO 1273 END SUBROUTINE YieldCheck
そこで,
もちろん,読者の判断によりこの値を変更しても差し支えないし,入力にする方法もあるであろう.