４．離散化解極限解析の入力データ

４－１　入力デー夕の種類

 これまで，面内変形平面問題におけるRBSMの理論的背景をFEMと比較しながら説明してきた．ここでは，これらの考え方をもとにプログラムを作成し実行する上で必要となる入力データについて説明する．
 現在，FEM解析は研究目的のみならず，設計計算から現場管理などの実用的な問題にも適用され，研究者から現場の技術者まで利用者の技術程度にかかわらず，数多くのユーザーが利用している．このようにユーザー層の据野が広がった理由は，その有効性のみならず扱い易さの点もあるであろう．良いか悪いかは別として，とにかくデータを入力しさえすれば答えがかえってくる．もちろん，要素分割はコンピュー夕ーが行つてくれるし，その要素分割が悪ければ修正まで自動的に行つてくれるプログラムもある．このようにユーザー層の広がりは数多くのデー夕加工処理プログラムを生み，その結果，さらにFEMに関するユーザー層が拡大していった．
 一方，RBSMは比較的新しい考え方であるため，専用のデータ加工処理プログラムはほとんどないに等しい．もし，FEM解析で育まれた膨大なソフトという財産を利用できれば，新たに開発してゆく時間や手間も省け，都合がよい．さらに，RBSMのデー夕構造をFEMのそれとできるだけ一致させ，RBSM独特のデー夕につていては可能なかぎり内部処理や後から付加するよう配慮すれば，利用者に余分な手間をかけないですみ，FEMとのデー夕の共有化が可能となる．
 そこで，このような点を考慮して，これまでの理論展開に基づき，離散化極限解析を行う際に必要となる入力データを整理してみよう．
（１）座標デー夕
 FEMと同様，RBSMにおいても解析領域を有限な要素に分割し，この要素を利用して離散化極限解析を行う．したがって，それらの要素を構成している節点の座標を入力しておかなければ要素形状を認識することはできない．RBSMの場合，節点に自由度を設けるわけではないので，有限要素法における節点の使われ方とは異なるが，単にデー夕構造としてこの節点データを捕らえた場合，FEMと全く同じと考えてよい．
 上のように，RBSMにおいても節点における $x$ 座標，$y$ 座標をFEMと同様に入力しなければならない．
 
$\hspace{5em}$図4.1　節点座標
（２）要素デー夕
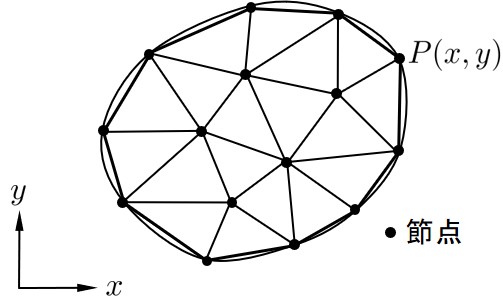
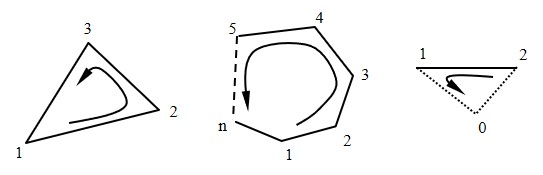
 要素の形状を認識するためには，各要素がどの節点から構成されているか要素を構成している節点番号を入力する必要がある．要素形状が図4.2(a)のように三角形の場合にはFEMにおける定ひずみ要素のデー夕構造と全く同じになる．
 
$\hspace{2em}$(a)三角形要素 $\hspace{3em}$(b)n角形要素 $\hspace{3em}$(c)境界用要素
$\hspace{7em}$図4.2　要素構成節点番号の読み方
 しかし，RBSMでは図(b)に示すようなn角形要素や，図(c)のような境界や載荷面に用いる境界用要素も使用できる．この場合にはFEMのデー夕構造と異なるが，特別な理由がないかぎりRBSMにおいても三角形や四角形要素を利用し，境界用の要素についてはインデックスを作成して後から付加する．このようにすると，要素データを作成する段階ではFEMのデータ構造と同じになる．
（３）材料データ
 弾性係数やポアソン比，強度定数など，RBSMにおいても要素単位で材料定数を指定する．ば ね定数や2要素間の強度定数については2.6節で示したように垂線を重みとしてプログラム内部で平均化し利用するため，FEMの場合と同じデータ構造となる．
（４）境界条件デー夕
 FEMでは通常，節点に変位の自由度を設定し，変位に関する拘束があればこの節点の変位を拘束する．一方，RBSMでは変位を拘束したい箇所に境界用要素を設け，その自由度を拘束することが通常行われている．したがって，FEMと全く異なったデータ構造となるが，流通しているデー夕加工処理プログラムの中には分布荷重を処理するため要素境界辺を指定できるプログラムもある．この技術を応用すればデータ構造は異なるがデー夕加工処理プログラムにより入力することができる．
（５）荷重デー夕
 境界条件デー夕と同様，通常，要素図心に荷重を載荷するため，節点に載荷するFEMとはデータ構造が異なる．しかし，境界条件に関する項でも述べたように分布荷重を処理する機能を利用すれば，デー夕加工処理プログラムにより作成は可能となる．
（６）ばねデータ
 RBSMでは2要素間の相対変位を利用してばね剛性行列を誘導しているが，このためには，各要素境界辺を共有する要素番号や節点番号を認識しておかなければならない．これはFEMには見られないデー夕である．しかし，このデー夕は要素データを基にプログラム内部で作成可能なデー夕であるため，入力の必要は無い．ただし，FEMにおけるジョイント要素のように接触面や不違続面の表現に使用する場合は，ばね定数を直接入力する必要が生じる．
（７）図心データ
 RBSMでは要素内の任意位置に自由度を設定する．本書ではその位置を要素図心にとっている．したがって，図心デー夕というより，むしろ，要素内の自由度設定位置と考えた方がよい．通常は図心という一定の規則を設けているため，プログラム内部で作成することができる．しかし，部分的にパラメー夕設定位置を変えたい場合には入力しなければならない．
（８）垂線データ
 仮想ひずみなどを計算する場合に必要となるデー夕で，よほど特別な理由がない限りプログラム内部で作成する．
 このように入力データの整理を行つてみると，FEMと同様なデー夕が多く，RBSM独特なデー夕についてはほとんどがプログラム内部で処理可能であるか，後から付加することが可能である．したがって，FEMにおけるデー夕加工処理プログラムの一部を修正したりすることによって，入力処理の半自動化が行える．
 
$\hspace{7em}$図4.3　入力部のフロー
 次に，離散化極限解析におけるデー夕処理部の簡単なプログラムフローを作成してみよう．図4.3に示す基本データの入力形式についてはプログラムを参照してほしい．この入力形式によるプログラムは8章のリスト142行～210行に掲載されているサブルーチン(InputData)である．読者なりの書式に変更したい場合にはこのサブルーチンを差し替えればよい．図4.3に従いプログラム化したものがプログラム4.1である．
 プログラム4.1　データ作成コントロール(Prepocessing) 

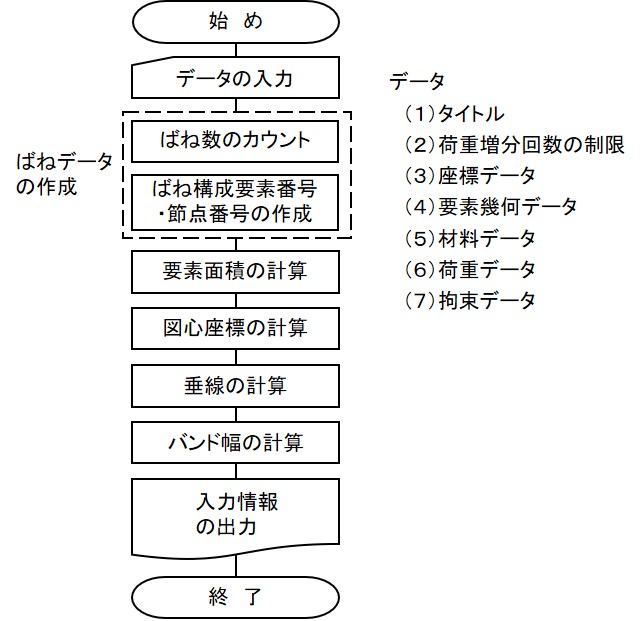
116	!===============================================================================
117	  SUBROUTINE Prepocessing( Title, Node, Element, Material, Spring, Load, &
118	                           Boundary, Nonlinear, Solver, File)
119	
120	    CHARACTER*80,       INTENT(OUT) :: Title
121	    TYPE(typeNode),     INTENT(OUT) :: Node
122	    TYPE(typeElement),  INTENT(OUT) :: Element
123	    TYPE(typeMaterial), INTENT(OUT) :: Material
124	    TYPE(typeSpring),   INTENT(OUT) :: Spring
125	    TYPE(typeLoad),     INTENT(OUT) :: Load
126	    TYPE(typeBoundary), INTENT(OUT) :: Boundary
127	    TYPE(typeNonLinear),INTENT(OUT) :: NonLinear
128	    TYPE(typeBand),     INTENT(OUT) :: Solver
129	    TYPE(typeFile),     INTENT(IN)  :: File
130	
131	    CALL InputData(Title,Node,Element,Material,Load,Boundary,Nonlinear,Solver,File)
132	    Spring%no = noSpring(Element)
133	    CALL SpringData(Element,Spring)
134	    CALL Area(Node,Element)
135	    CALL gCenter(Node,Element)
136	    CALL Perpendicular(Node,Element,Spring)
137	    Solver%width = BandWidth(Element,Spring)
138	    CALL PrintData(Title,Node,Element,Material,Spring,Load,Boundary,Nonlinear, &
139	                   Solver,File)
140	  END SUBROUTINE Prepocessing
 それぞれのサブルーチンの役割は8章に示してある．関数(noSpring)及びサブルーチン(SpringData)でばねデータが作成される．このことについては次節においてさらに詳しく述べることにする．
 サブルーチン(Area)は三角形の要素面積を計算するためのプログラムで，FEMでも利用されているのでここでは説明を省略する．ただし，329行（8章参照）にあるIF文で境界用要素を識別し，もし境界用の要素であれば面積を0としている．

４－２　ばねデータの作成

 構造物や地盤などの崩壊解析を行う際に問題となるのが破壊基準の考え方である．先にも述べたようにRBSM特有のデー夕として，ばねの位置を認識するデー夕があげられる．このデータを手作業で入力することは，当然のこととして手間がかかるし，それにも増して入力ミスを誘い易いため，できるだけプログラム内部で作成したほうがよい．本書に掲載したサンプル・プログラムでは，このようなばねデー夕の作成を2つのプログラムにより行っている．
 一つは関数(noSpring)で，このプログラムではばね数をカウントしている．よほど特殊な場合でないかぎり，一つのばねは2つの要素のみ共有する．プログラム4.2はその例である．229行において2つの要素が共有する節点数を(same)という変数により調べ，この値が2のときばねが存在すると考える．もし，この値が3であれば，それは2つの要素が全く同じ要素構成節点番号を持っていることになり，明らかに要素デー夕にミスがある．また，1以下の場合はデータのミスではなく，共有する要素境界辺が存在していないことを意味する．
 プログラム4.2　ばね数のカウント(noSpring) 

211	!-------------------------------------------------------------------------------
212	  FUNCTION noSpring( Element ) RESULT( no )
213	
214	    TYPE(typeElement), INTENT(IN) :: Element
215	    INTEGER :: no
216	
217	    INTEGER :: ie,je,same,edge,error,i,j
218	
219	    no    = 0
220	    error = 0
221	    DO ie = 1, Element%no - 1 
222	      edge = 0 
223	      DO je = ie+1, Element%no
224	        same = 0
225	        DO i = 1, 3
226	          IF(Element%node(i,ie) /= 0) THEN
227	            DO j = 1, 3
228	              IF(Element%node(i,ie) == Element%node(j,je)) THEN
229	                same = same + 1
230	              END IF
231	            END DO
232	          END IF
233	        END DO
234	        IF(same > 2) THEN
235	          error = error + 1
236	          PRINT 6000, ie,je
237	          6000 FORMAT(/,' *** ERROR *** SAME NODE  ELEM. NO.(',I3,',',I3,')')
238	         ELSE IF(same == 2) THEN
239	          no = no + 1
240	          edge = edge + 1
241	        END IF
242	      END DO
243	      IF(edge > 3) THEN
244	        error = error + 1
245	        PRINT 6010, ie,(Element%node(i,ie),i=1,3)
246	        6010 FORMAT(/,' *** ERROR *** NODE DATA  ELEM. NO.',I3, &
247	                      '  NODE NO.(',I3,',',I3,',',I3,')')
248	      END IF
249	    END DO    
250	    IF(error == 0) RETURN
251	    STOP 100
252	  END FUNCTION noSpring
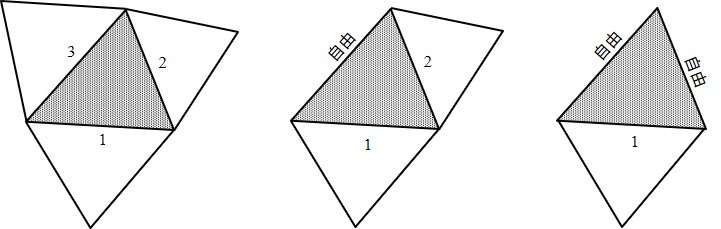
 本プログラムでは境界用の要素の他は，三角形要素のみを考えている．したがって，一つの要素において，要素境界辺は3以下でなければならない．このことを図に示したものが図4.4である．図に示すように，境界用要素と三角形要素のみ利用する場合はばねが生ずる位置として図(a)(b)(c)の3ケースが考えられる．もし，3以上の要素境界辺が有つたならそれは明かにデータに誤りがあることになる．なお，本プログラムではばね数を(Spring%no)という変数により表現している．その他の変数については，8章のプログラムリストを参照してほしい．
 
$\hspace{1em}$(a)3辺共有 $\hspace{4em}$(b)2辺共有 $\hspace{3em}$(c)1辺共有
$\hspace{2em}$図4.4　ある要素が共有する境界辺のタイプ
 ばねは要素境界辺を共有する2つの要素番号とその辺を構成する節点番号で特定する．前者のデータは(Spring%element)という配列に，後者のデータは，(Spring%node)という配列に格納している．これらの作業はプログラム4.3に示すサブルーチン(SpringData)により行っている．2次元問題の場合，ばね構成節点数は2であり，そり以上でも以下でもない．ここで，注意をしなければいけないことは図4.5に示すように，ばね構成節点番号における順番がばね構成要素番号の1番目の要素に支配されていることである．すなわち，(Spring%element)に格納された1番目の要素に着目し，その要素からみ見て反時計回りにばね構成節点番号を作成しなければならない．なぜこのように考えるかというと，相対変位や表面力を計算する場合に使用する，要素境界辺上に設けた法線方向をこの(Spring%no)から決定するからである．このように考えておけば，得られる表面力は引っ張りが正，圧縮が負となる．
 
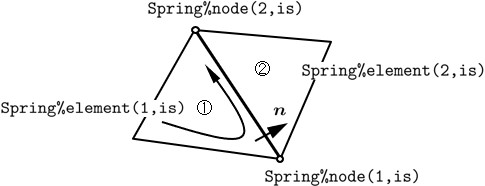
$\hspace{8em}$図4.5　ばね構成節点番号の考え方
 プログラム4.3　ばねデータ（ばね構成要素・節点番号の作成）(SpringData) 

253	!-------------------------------------------------------------------------------
254	  SUBROUTINE SpringData( Element, Spring ) 
255	
256	    TYPE(typeElement),  INTENT(IN)    :: Element
257	    TYPE(typeSpring),   INTENT(INOUT) :: Spring
258	
259	    INTEGER :: no,is,ie,je,in,jn,n1,n2,same,i,j,ibit
260	
261	    ALLOCATE( Spring%node(2,Spring%no) )
262	    ALLOCATE( Spring%element(2,Spring%no) )
263	    ALLOCATE( Spring%length(Spring%no) )
264	    ALLOCATE( Spring%hline(2,Spring%no) )
265	    ALLOCATE( Spring%flag(Spring%no) )
266	    ALLOCATE( Spring%strain(2,Spring%no) )
267	    ALLOCATE( Spring%dstrain(2,Spring%no) )
268	    ALLOCATE( Spring%stress(2,Spring%no) )
269	    ALLOCATE( Spring%dstress(2,Spring%no) )
270	
271	    no = 0
272	    DO ie = 1, Element%no - 1
273	      DO je = ie+1, Element%no
274	        same = 0
275	        DO i = 1, 3
276	          IF(Element%node(i,ie) /= 0) THEN
277	            DO j = 1, 3
278	              IF(Element%node(i,ie) == Element%node(j,je)) THEN
279	                same = same + 1 
280	              END IF
281	            END DO
282	          END IF
283	        END DO
284	        IF(same == 2) THEN
285	          no = no + 1
286	          Spring%element(1,no) = ie
287	          Spring%element(2,no) = je
288	        END IF
289	      END DO
290	    END DO    
291	    Loop : DO is = 1, Spring%no
292	      ie = Spring%element(1,is)
293	      je = Spring%element(2,is)
294	      DO i = 1, 3
295	        in = Element%node(i,ie)
296	        ibit = 0
297	        DO j = 1, 3
298	          jn = Element%node(j,je)
299	          IF(in == jn) THEN
300	            ibit = 1
301	          END IF
302	        END DO
303	        IF(ibit == 0) THEN
304	          n1 = i + 1
305	          n2 = i + 2
306	          IF(n1 > 3) n1 = n1 - 3
307	          IF(n2 > 3) n2 = n2 - 3
308	          Spring%node(1,is) = Element%node(n1,ie)
309	          Spring%node(2,is) = Element%node(n2,ie)
310	          CYCLE Loop
311	        END IF
312	      END DO
313	    END DO Loop
314	  END SUBROUTINE SpringData
 本書に掲載したばね発生プログラムは参考例であり，他にも考え方はあるであろう．必要に応じて読者なりのプログラムを開発したらよい．ただし，先に示したばね構成節点番号の付け方に対しては十分な注意が必要である．

４－３　図心の計算

 FEMでは各節点に自由度を設定するため，座標デー夕として節点の座標値を読み込むことで必然的に自由度の位置が入力されたのと同じことになるが，RBSMでは要素内の任意の位置に自由度を設定するため，その位置を指定しておかなければならない．本書ではその位置を図心にとっている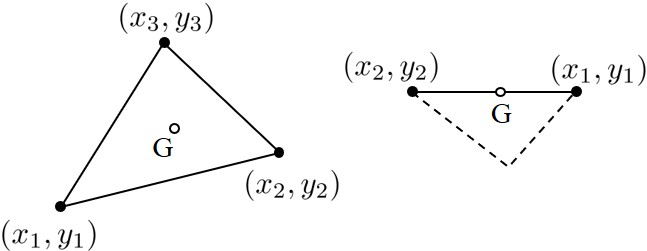．プログラム4.4は各要素の図心を計算するプログラムである．変数(Element%center)が要素の図心座標を示しており，三角形の場合，図4.6より以下のように計算される．
 
$\hspace{3em}$(a)三角形要素 $\hspace{5em}$(b)境界用要素
$\hspace{8em}$図4.6　図心の計算
 プログラム4.4　図心座標の計算(gCenter) 

349	!-------------------------------------------------------------------------------
350	  SUBROUTINE gCenter( Node, Element )
351	
352	    TYPE(typeNode),     INTENT(IN)    :: Node
353	    TYPE(typeElement),  INTENT(INOUT) :: Element
354	
355	    INTEGER :: ie,n,i
356	    REAL(8) :: ww,wx,wy
357	
358	    DO ie = 1, Element%no
359	      ww = 0.0
360	      wx = 0.0
361	      wy = 0.0
362	      DO i = 1, 3
363	        n = Element%node(i,ie)
364	        IF(n /= 0) THEN
365	          ww = ww + 1
366	          wx = wx + Node%coord(1,n)
367	          wy = wy + Node%coord(2,n)
368	        END IF
369	      END DO
370	      Element%center(1,ie) = wx/ww
371	      Element%center(2,ie) = wy/ww
372	    END DO
373	  END SUBROUTINE gCenter
\[{\rm (4.1)}   x_{_G}=\frac{x_1+x_2+x_3}{3} \;\;\;\; y_{_G}=\frac{y_1+y_2+y_3}{3} \]
ただし，境界用の要素については364行の判定文により以下のように考える． \[{\rm (4.2)}   x_{_G}=\frac{x_1+x_2}{2} \;\;\;\; y_{_G}=\frac{y_1+y_2}{2} \]
境界用要素では3番目の節点が存在しないため，このように中点をとる．もし，境界用の要素における自由度の設定位置を目的に応じて入力するか，あるいは別な方法により計算で求める場合には本サブルーチン(gCenter)を変更すればよい．以上からも理解されるように，図心座標は通常要素単位で計算される．

４－４　垂線の計算

 RBSMではばね定数を決定するため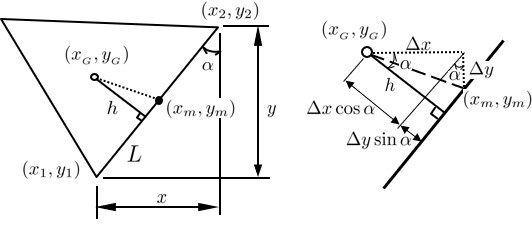，2.3節で説明したように垂線を利用している．このような計算はFEMでは見られない．垂線は1つの要素境界辺に対して2つの要素が関係しているため，各要素境界辺に対し①要素側と②要素側の2つを計算しなければならない．図4.7はこの計算過程を図化したものである．
 
$\hspace{8em}$図4.7　垂線の計算
 初めに要素境界辺の傾きを以下の式により求める．ここで，$L$ は境界辺の長さである．
\[{\rm (4.3)}   m=\sin \alpha=\frac{x}{L} \;\;\;\; l=\cos \alpha=\frac{y}{L} \]
次に，要素図心の座標 $(x_G, y_G)$ から要素境界辺上の中点 $(x_m, y_m)$ に結んだ線 $\overline{GM}$ の $x$ 方向成分，$y$ 方向成分を
\[{\rm (4.4)}   \Delta x=x_{_m} - x_{_G} \;\;\;\; \Delta y=y_{_m} - y_{_G} \]
のごとく計算し，この成分をさらに法線方向へ座標変換することによって垂線を以下のように計算することができる．
\[ h = \Delta x \cdot l - \Delta y \cdot m \]
 これをプログラム化したものがプログラム4.5のサブルーチン(Perpendicular)である．変数(Spring%hline)には垂線の値が記憶されており，396行～398行で①要素側の垂線 $h_1$ を計算し，399行～401行で②要素側の垂線 $h_2$ を計算している．
 プログラム4.5　垂線の計算(Perpendicular) 

374	!-------------------------------------------------------------------------------
375	  SUBROUTINE Perpendicular( Node, Element, Spring ) 
376	
377	    TYPE(typeNode),    INTENT(IN)    :: Node
378	    TYPE(typeElement), INTENT(IN)    :: Element
379	    TYPE(typeSpring),  INTENT(INOUT) :: Spring 
380	
381	    INTEGER :: is,n1,n2,e1,e2
382	    REAL(8) :: sl,sm,xm,ym,h1,h2,x,y,xl,yl
383	
384	    DO is = 1, Spring%no
385	      n1 = Spring%node(1,is)
386	      n2 = Spring%node(2,is)
387	      x  = Node%coord(1,n2) - Node%coord(1,n1)
388	      y  = Node%coord(2,n2) - Node%coord(2,n1)
389	      Spring%length(is) = DSQRT(x*x+y*y)
390	      sl = y/Spring%length(is)
391	      sm = x/Spring%length(is)
392	      xm = (Node%coord(1,n1) + Node%coord(1,n2)) /2.D0
393	      ym = (Node%coord(2,n1) + Node%coord(2,n2)) /2.D0
394	      e1 = Spring%element(1,is)
395	      e2 = Spring%element(2,is)
396	      xl = xm - Element%center(1,e1)
397	      yl = ym - Element%center(2,e1)
398	      h1 = sl*xl - sm*yl
399	      xl = Element%center(1,e2) - xm
400	      yl = Element%center(2,e2) - ym
401	      h2 = sl*xl - sm*yl
402	      Spring%hline(1,is) = ABS(h1)
403	      Spring%hline(2,is) = ABS(h2)
404	    END DO
405	  END SUBROUTINE Perpendicular
 本プログラムでは図心に自由度を設定した場合の垂線を計算しているが，図心以外に自由度を設けた場合は変数(Element%center)にその点の座標を入れておけば，そのまま本サブルーチンにより垂線を計算することができる．また，垂線の考え方を変えたい場合はこのサブルーチンを変更すればよい．

４－５　バンド幅の考え方

 本プログラムでは連立方程式の計算に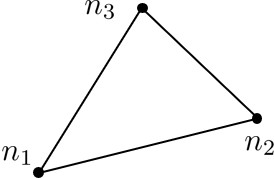変形コレスキー法を用いたバンド法を利用している．このためには，バンド幅の計算が必要になる．ここでは，このことについて補足しておく．
 
図4.8　三角形の頂点における節点番号
 FEMの定ひずみ要素では三角形の頂点における節点番号を図4.8に示すよう $(n1,n2,n3)$とした場合，バンド幅は以下のように計算される．
\[{\rm (4.5)}   バンド幅 = \left\{ {\rm max(n_1,n_2,n_3) - min(n_1,n_2,n_3) } + 1 \right\} \times 2 \]
ここで，最後の2は各節点で $(u,v)$ の2自由度を持つているためである．
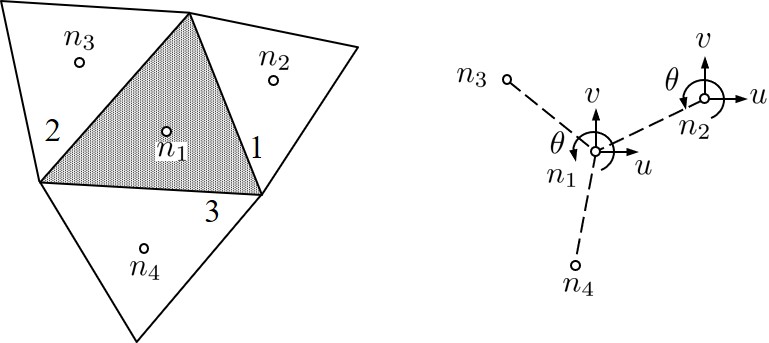
 ところが，RBSMでは剛体変位場を仮定しているため，節点ではなく要素内の任意の位置に $(u,v,\theta)$ の3自由度を考える．そして，2要素間の境界辺に設けたばねにより2つの要素を関係付け，要素剛性行列を作成する．したがって，FEMにおける節点に対応するのが要素内に設けた自由度点であり，これを図4.9(b)に示すように模式化して考えるとRBSMにおけるバンド幅が以下のように計算できる．
 
$\hspace{3em}$(a)自由度設定位置 $\hspace{5em}$(b)ばねの自由度
$\hspace{7em}$図4.9　RBSMにおけるバンド幅
\[{\rm (4.6)}   バンド幅 = \left( \left| {\rm n_1 - n_2} \right| + 1 \right) \times 3 \]
ここで，最後の3は各要素の自由度が3であることを意味している．すなわち，ばねに関係する2要素の要素番号の差に対する絶対値に対角項分1を加え，その数に各要素の自由度3を掛けたものがバンド幅と定義される．もちろん，系全体のバンド幅を考えるべきであるから，実際のバンド幅は式(4.6)をすべてのばねについて求め，その内の最大のものとなる．このバンド幅を用いた剛性行列の組立については次章においてさらに説明を加える．
 以上の関係をプログラム化したものがプログラム4.6の関数(BandWidth)である．ばねに関係する要素番号が変数(Spring%element)に格納されているから，この配列を利用して416行に示すよう，バンド幅を計算する．この計算を全てのばねについて行い，一番大きな値をもって，その系におけるバンド幅とする．プログラムでは変数(Solver%width)により系全体のバンド幅を定義している．
 プログラム4.6　バンド幅の計算(BandWidth) 

406	!-------------------------------------------------------------------------------
407	  FUNCTION BandWidth( Element, Spring ) RESULT( width )
408	
409	    TYPE(typeElement), INTENT(IN) :: Element
410	    TYPE(typeSpring),  INTENT(IN) :: Spring
411	
412	    INTEGER :: width,is,wd
413	
414	    width = 0
415	    DO is = 1, Spring%no
416	      wd = Spring%element(2,is) - Spring%element(1,is)
417	      IF(wd > width) THEN
418	        width = wd
419	      END IF
420	    END DO
421	    width = (width+1)*Element%dof
422	    ALLOCATE( Solver%stiff(Solver%no*width) )
423	    ALLOCATE( Solver%load(Solver%no) )
424	  END FUNCTION BandWidth