３．非線形解析法

３－１　破壊条件

 構造物や地盤などの崩壊解析を行う際に問題となるのが破壊基準の考え方である．最近では実験技術の進歩に伴い，理論的な破壊基準以外にも実験式的な基準が数多く提案されている．これらの基準をすべて数値解析に取り入れることができるかというと，アルゴリズムとの適合性などから必ずしもそうでないモデルもあるようである．本書ではRBSMによる離散化極限解析に破壊条件をどのように取り込むかを主に説明するため，代表的な二三の破壊条件を示し，それらに対してどのように構成式を誘導するかを説明する．基本的には最近発表されている多くの破壊基準式に対しても同様な手法により導入することが可能である．
 RBSMではFEMのように要素内応力ではなく，要素境界辺上における垂直方向及びせん断方向に関する2つの単位面積当りの表面力を取り扱う．したがって，破壊条件としては合力で与えられる式を直接利用する．すなわち，FEMではテンソル量としての応力から主応力などを利用して破壊条件式を考えるのに対し，RBSMではベクトル量としての合力によって破壊条件を表す．この点さえ注意を行えば，その後の展開はFEMにおける取り扱いと大差ない．
 以下に本書で取り扱う破壊条件式を整理しておき，詳細についての説明は専門書に譲る．
（１）トレス力の条件
 図3.1(a)に示されているように，トレスカの条件ではせん断応力 $\tau$ が垂直応力 $\sigma$ に関係なく，せん断強度 $C$ を越えたら破壊するものと考える．この関係を式で表すと，降伏関数を $f$ として以下のようになる．
\[{\rm (3.1)}   \left. \begin{array}{l} \tau = \pm C \\ f = \tau^2 - C^2 \end{array} \right\} \]
 
$\hspace{0em}$(a)トレスカの条件 $\hspace{4em}$(b)クーロンの条件
$\hspace{3em}$図3.1　平面ひずみ状態の降伏条件
（２）クーロンの条件
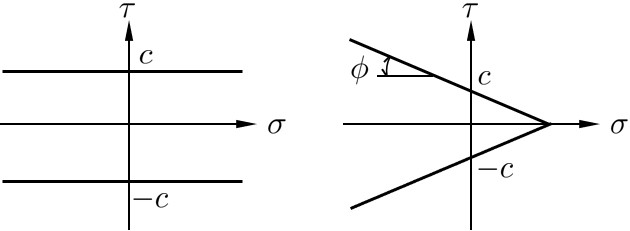
 クーロンの条件は図3.1(b)に示すように，せん断応力 $\tau$ が垂直応力 $\sigma$ の1次関数となっている場合で，内部摩擦角を $\phi$ としたとき以下のように与えられる．
\[{\rm (3.2)}   \left. \begin{array}{l} \tau = \pm ( C - \tan \phi \cdot \sigma) \\ f = \tau^2 - (C-\tan \phi \cdot \sigma)^2 \end{array} \right\} \]
ただし，式(3.2)では引っ張り方向の垂直応力を正と考えている．なお，上記二つの降伏条件は平面ひずみ状態を仮定した場合の式である．
（３）ミーゼスの条件
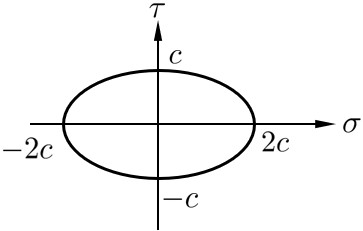
 次に，平面応力状態の代表的な降伏条件として以下のようなミーゼスの条件を示す． \[{\rm (3.3)}   \left. \begin{array}{l} \displaystyle \tau^2 + \frac{1}{4} \sigma^2 = C^2 \\[1em] \displaystyle f = \tau^2 + \frac{1}{4}\sigma^2 - C^2 \end{array} \right\} \]
ここに，$C$ はせん断降伏応力である．
 なお，本書では面内変形平面問題を対象としているため，3次元問題や軸対称問題，梁要素に関する降伏条件については省略する．
 
図3.2　ミーゼスの降伏条件

３－２　構成方程式

 RBSMで取り扱う垂直及びせん断に関する表面力は2種類のばねを通して各要素に伝わる．一旦，このばねの受け持つ力が前節で示した降伏条件に達するとすべりなどの破壊が発生し，その後，破壊条件を満足しながら表面力が増加，減少する．本節ではこのような現象を表現するための構成式について説明する．塑性理論においては，降伏面を応力空間の表面として定義する降伏関数と塑性ひずみ増分の成分を定義する塑性ポテンシャル関数の二つの関数が存在していると仮定している．
 前者の降伏面は弾性ひずみが生ずる応力状態と弾性ひずみと塑性ひずみの両者が混在する応力状態の境界に存在し，一般に
\[{\rm (3.4)}   f( \boldsymbol{\sigma} , \boldsymbol{\varepsilon}^p ) = 0 \]
と表される．
 一方，後者の塑性ポテンシャルは，その勾配によってひずみ増分の方向を定義しており，一般には
\[{\rm (3.5)}   Q( \boldsymbol{\sigma} )= 0 \]
と書き表せる．通常，降伏関数と塑性ポテンシャルが等しいとする関連流れ則を用いているが，土のダイラタンシーを表現する場合などでは，これらが等しくないとする非関連流れ則を用いる必要がある．この場合は構成式が対称行列にならず，数値計算上何らかの対策が必要である．本書では，問題の簡略化のため，式(3.6)に示す条件を満足する関連流れ則を用いる．
\[{\rm (3.6)}   f \equiv Q \]
 いま，塑性ポテンシャル $Q$ を
\[{\rm (3.7)}   Q( \boldsymbol{\sigma} ) = 0    \boldsymbol{\sigma} = \left(\sigma_n, \tau \right) \]
とすれば，塑性流れ則に従い，塑性化後のひずみ増分 $\Delta \boldsymbol{\varepsilon}^{(p)}$ は
\[{\rm (3.8)}   \Delta \boldsymbol{\varepsilon}^{(p)} = \lambda \frac{\partial Q}{\partial \boldsymbol{\sigma}} = \left( \varepsilon_n^{(p)} , \gamma^{(p)} \right) \]
と表せる．ここで，上付きの $(p)$ は塑性状態の量を，$\Delta$ は増分量であることを示す．$\lambda$ は比例定数で，関連流れ則に従うならばひずみの方向は塑性ポテンシャル $Q$ に対して，すなわち，降伏面 $f$ に対して垂直になる．
 また，弾性状態の量を上付きの $(e)$ で表せば，ひずみは
\[{\rm (3.9)}   \Delta \boldsymbol{\varepsilon}^{(e)} = \Delta \boldsymbol{\varepsilon} - \Delta \boldsymbol{\varepsilon}^{(p)} \]
と表せる．ここで，$\boldsymbol{\varepsilon}$ は全ひずみを示している．
 一方，弾性時における応力とひずみの間には次の関係が成立している．
\[{\rm (3.10)}   \boldsymbol{\sigma} = \boldsymbol{D}^{(e)} \cdot \boldsymbol{\varepsilon}^{(e)} \]
 したがって，式(3.10)は式(3.8)，式(3.9)より増分形式により次のように表せる．
\[{\rm (3.11)}   \Delta \boldsymbol{\sigma} = \boldsymbol{D}^{(e)} \left( \Delta \boldsymbol{\varepsilon} - \lambda \frac{\partial Q}{\partial \boldsymbol{\sigma}} \right) \]
さらに，式(3.l1)を塑性条件
\[{\rm (3.12)}   \frac{\partial f}{\partial \boldsymbol{\sigma}} \Delta \boldsymbol{\sigma} = 0 \]
に代入し，$\lambda$ について解くと以下の関係が得られる．
\[{\rm (3.13)}   \lambda = \frac{\displaystyle \frac{\partial f}{\partial \boldsymbol{\sigma}} \cdot \boldsymbol{D}^{(e)} \cdot \Delta \boldsymbol{\varepsilon} } {\displaystyle \frac{\partial f}{\partial \boldsymbol{\sigma}} \boldsymbol{D}^{(e)} \frac{\partial Q}{\partial \boldsymbol{\sigma}} } \]
式(3.13)を式(3.11)に代入すれば，次のような増分表面力の関係式が得られる．
\[{\rm (3.14)}   \Delta \boldsymbol{\sigma} = \left( \boldsymbol{D}^{(e)} - \frac{\displaystyle \boldsymbol{D}^{(e)} \frac{\partial f}{\partial \boldsymbol{\sigma}} \frac{\partial Q}{\partial \boldsymbol{\sigma}} \boldsymbol{D}^{(e)} } {\displaystyle \frac{\partial f}{\partial \boldsymbol{\sigma}} \boldsymbol{D}^{(e)} \frac{\partial Q}{\partial \boldsymbol{\sigma}} } \right) \Delta \boldsymbol{\varepsilon} \]
なお，本式にはひずみ硬化などの影響は含まれていない．式(3.14)は破壊条件に対する表面力と相対変位の比例関係のような取り扱いとなっている．
 式(3.l4)から塑性化後のばね行列を成分表示すると，
\[{\rm (3.15)}   K_{ij}^{(p)} = K_{ij}^{(e)} \cdot \delta_{ij} - \frac{1}{\sum K_i^{(e)} \cdot f_i^2} f_i \cdot f_j \cdot K_i^{(e)} \cdot K_j^{(e)} \]
\[\hspace{7em} f_i = \frac{\partial f}{\partial \sigma_i}    \sigma_i = \left(\sigma_n, \tau \right) \]
となる．ここで，$\delta_{ij}$ はクロネッカーのデル夕であり，$K_{ij}^{(e)}$ は弾性時におけるばねの成分を表している．
 塑性解析では除荷過程を取り入れる必要がある．この判定を厳密に行うためには塑性仕事増分を用いて行わなければならないが，近似的には $\lambda \lt 0$ により行つてもよい．
 以下にそれぞれの破壊条件を用いた場合の構成式を誘導する．
（１）トレス力の条件
  降伏関数 $\hspace{4em}$ $ f = \tau^2 - C^2$
  降伏条件 $\hspace{4em}$ $ f = 0$
  塑性流れ則 $\hspace{3em}$ $ \Delta \varepsilon_n^{(p)} = \lambda \frac{\displaystyle \partial f}{\displaystyle \partial \sigma_n} $ $\hspace{2em}$ $ \Delta \gamma^{(p)} = \lambda \frac{\displaystyle \partial f}{\displaystyle \partial \tau} $
  ひずみ増分 $\hspace{3em}$ $ \Delta \varepsilon_n^{(e)} = \Delta \varepsilon_n - \Delta \varepsilon_n^{(p)} $
$\hspace{10em}$ $ \Delta \gamma^{(e)} = \Delta \gamma - \Delta \gamma^{(p)} $
  応力－ひずみ関係（力－相対変位関係）
\[\hspace{8em} \left\{ \begin{array}{c} \Delta \sigma_n \\ \Delta \tau \end{array} \right\} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \left\{ \begin{array}{c} \Delta \varepsilon_n^{(e)} \\ \Delta \gamma^{(e)} \end{array} \right\} \]   塑性条件 $\hspace{4em}$ $ \frac{\displaystyle \partial f}{\displaystyle \partial \sigma_n} \cdot \Delta \sigma_n + \frac{\displaystyle \partial f}{\displaystyle \partial \tau} \cdot \Delta \tau = 0 $
以上を整理すると，$\lambda$ が以下のように計算される．
\[\hspace{2em} \lambda = \frac{\Delta \gamma}{2 \tau} \]
したがって，塑性化後の構成式は以下のようになる．
\[{\rm (3.16)}   \Delta \boldsymbol{\sigma} = \boldsymbol{D}^{(p)} \cdot \Delta \boldsymbol{\varepsilon} \] \[\hspace{6em} \boldsymbol{D}^{(p)} = \boldsymbol{D}^{(e)} - \boldsymbol{S} \]
\[\hspace{6em} \boldsymbol{D}^{(e)} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \hspace{2em} \boldsymbol{S} = \left[ \begin{array}{cc} 0 & 0 \\ 0 & E_2 \end{array} \right] \]
式(3.16)をよく眺めると，塑性化後にせん断ばねを切断すればよいことがわかる．RBSMではこのように簡単な手続きで塑性解析が可能となる．なお，式(3.l6)に現れる $E_1$，$E_2$ は平面ひずみ及び平面応力状態により，それぞれ，式(2.12)，式(2.13)に示す値を取る．また，ばねとの関係は以下の通りである．
\[\hspace{2em} k_n = \frac{E_1}{h_1+h_2} \hspace{2em} k_s = \frac{E_2}{h_1+h_2} \]
ここで， $h_1, h_2$ は各要素の垂線である．
（２）ク一口ンの条件
  降伏関数 $\hspace{4em}$ $ f=\tau^2 - (C-\tan \phi \cdot \sigma_n)^2 $
  降伏条件 $\hspace{4em}$ $ f=0 $
  塑性流れ則 $\hspace{3em}$ $ \Delta \varepsilon_n^{(p)} = \lambda \displaystyle \frac{\partial f}{\partial \sigma_n} $ $\hspace{2em}$ $ \Delta \gamma^{(p)} = \lambda \displaystyle \frac{\partial f}{\partial \tau} $
  ひずみ増分 $\hspace{3em}$ $ \Delta \varepsilon_n^{(e)} = \Delta \varepsilon_n - \Delta \varepsilon_n^{(p)} $
$\hspace{10em}$ $ \Delta \gamma^{(e)}=\Delta \gamma - \Delta \gamma^{(p)} $
  応力－ひずみ関係（力－相対変位関係）
\[\hspace{8em} \left\{ \begin{array}{c} \Delta \sigma_n \\ \Delta \tau \end{array} \right\} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \left\{ \begin{array}{c} \Delta \varepsilon_n^{(e)} \\ \Delta \gamma^{(e)} \end{array} \right\} \]   塑性条件 $\hspace{4em}$ $ \displaystyle \frac{\partial f}{\partial \sigma_n} \cdot \Delta \sigma_n + \frac{\partial f}{\partial \tau} \cdot \Delta \tau = 0 $
以上を整理すると，$\lambda$ が以下のように計算される．
\[\hspace{2em} \lambda = \frac{1}{F} \left\{ E_2 \cdot \tau \cdot \Delta \gamma + E_1 ( c - \tan \phi \cdot \sigma_n) \tan \phi \cdot \Delta \varepsilon_n \right\} \] \[\hspace{4em} F = E_2 \cdot \tau^2 + E_1 \left\{ (c-\tan \phi \cdot \sigma_n) \tan \phi \right\}^2 \]
したがって，塑性化後の構成式は以下のようになる．
\[{\rm (3.17)}   \Delta \boldsymbol{\sigma} = \boldsymbol{D}^{(p)} \cdot \Delta \boldsymbol{\varepsilon} \] \[\hspace{6em} \boldsymbol{D}^{(p)} = \boldsymbol{D}^{(e)} - \boldsymbol{S} \]
\[\hspace{6em} \boldsymbol{D}^{(e)} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \] \[\hspace{6em} \boldsymbol{S} = \frac{1}{F} \left[ \begin{array}{cc} E_1^2 \left\{ C-\tan \phi \cdot \sigma_n) \tan \phi \right\}^2 & E_1 E_2 \tau ( C-\tan \phi \cdot \sigma_n) \tan \phi \\ {\rm sym.} & E_2^2 \cdot \tau^2 \end{array} \right] \]
（３）ミーゼスの条件
  降伏関数 $\hspace{4em}$ $ f = \tau^2 + \frac{1}{4}\sigma^2 - C^2 $
  降伏条件 $\hspace{4em}$ $ f = 0 $
  塑性流れ則 $\hspace{3em}$ $ \Delta \varepsilon_n^{(p)} = \lambda \displaystyle \frac{\partial f}{\partial \sigma_n} $ $\hspace{2em}$ $ \Delta \gamma^{(p)} = \lambda \displaystyle \frac{\partial f}{\partial \tau} $
  ひずみ増分 $\hspace{3em}$ $ \Delta \varepsilon_n^{(e)} = \Delta \varepsilon_n - \Delta \varepsilon_n^{(p)} $
$\hspace{10em}$ $ \Delta \gamma^{(e)}=\Delta \gamma - \Delta \gamma^{(p)} $
  応力－ひずみ関係（力－相対変位関係）
\[\hspace{8em} \left\{ \begin{array}{c} \Delta \sigma_n \\ \Delta \tau \end{array} \right\} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \left\{ \begin{array}{c} \Delta \varepsilon_n^{(e)} \\ \Delta \gamma^{(e)} \end{array} \right\} \]   塑性条件 $\hspace{4em}$ $ \displaystyle \frac{\partial f}{\partial \sigma_n} \cdot \Delta \sigma_n + \displaystyle \frac{\partial f}{\partial \tau} \cdot \Delta \tau = 0 $
以上を整理すると，$\lambda$ が以下のように計算される．
\[\hspace{2em} \lambda = \frac{1}{F} \left( E_1 \cdot \frac{\sigma_n}{2} \cdot \Delta \varepsilon_n + 2 E_2 \cdot \tau \cdot \Delta \gamma \right) \] \[\hspace{4em} F = \left( \frac{1}{4} E_1 \cdot \sigma_n^2 + 4 E_2 \cdot \tau^2 \right) \]
したがって，塑性化後の構成式は以下のようになる．
\[{\rm (3.17)}   \Delta \boldsymbol{\sigma} = \boldsymbol{D}^{(p)} \cdot \Delta \boldsymbol{\varepsilon} \] \[\hspace{6em} \boldsymbol{D}^{(p)} = \boldsymbol{D}^{(e)} - \boldsymbol{S} \]
\[\hspace{6em} \boldsymbol{D}^{(e)} = \left[ \begin{array}{cc} E_1 & 0 \\ 0 & E_2 \end{array} \right] \] \[\hspace{6em} \boldsymbol{S} = \frac{1}{F} \left[ \begin{array}{cc} \frac{1}{4} E_1^2 \cdot \sigma_n^2 & E_1 \cdot E_2 \cdot \tau \cdot \sigma_n \\[1em] {\rm sym.} & 4E_2^2 \cdot \tau^2 \end{array} \right] \]
 トレスカの条件ではせん断ばねを切断する，すなわち， $k_s=0$ とすることによって塑性化後の構成式を表現することができた．しかし，一般的には構成式の非対角項が0でなくなるため，2章で示した剛性行列を使用できなくなる．
 そこで，塑性化後の剛性行列も弾性時の剛性行列と同様，陽な形で求めておく必要がある．これについては8章に結果のみを示しておく．

３－３　非線形計算法

 非線形性には材料的なものと幾何学的なものの2種類がある．前者の材料非線形性においても，クリープなどに代表される時間依存性の問題とそうでない問題に分けられる．本書ではこれらのうち時間に依存しない材料非線形問題の取り扱いについて述べる．
 材料非線形問題の数値計算法については，これまで多くの方法が提案されてきた．特にマトリックスを用いるFEMでは，その性質を巧みに利用した研究も数多く発表されている．どの方法を用いるかは解析モデルとの適応性や問題の性質にもよるため，一概に述べることはできないが，少なくとも，数値計算を行う場合には組織的なアルゴリズムとなるよう心がけなければならない．
 一般的な非線形計算法は大きく以下の3つに分類することができる．
 (1)の荷重増分法では，目的とする荷重をいくつかの小さな増分に分割し，各荷重増分段階において，剛性を変えることなく線形計算を行う．各荷重増分段階で得られた増分変位及び増分ひずみ，増分応力はそれまでの値に加えられ，今回の全変位，全ひずみ，全応力とする．剛性は1つ前の，すなわち，前回の荷重増分段階の応力状態から決定する．このように荷重増分法は非線形問題を近似的に線形問題の積み重ねとして解析する方法である．
 一方，(2)の反復法は全荷重下で解がつり合い状態を満足するまで収束計算を行う方法である．この方法は構造物などが崩壊する荷重値近傍では収束性が悪くなるが，部分的な塑性域を調べるためには有効な方法である．このような欠点を補うため，修正Newton-Raphson法などのような改良が行われている．ただし，全荷重を一度に作用させるため，荷重増分に伴う応力や変形の経路を知ることはできない．
 これら，両者の欠点を補った方法が混合法であり，増分法と反復法を組み合わせたものとなっている．
 以上のような非線形計算法については専門書に譲り，本書ではあまり深く触れない．
 さて，RBSMでは崩壊荷重や破壊パターンの解析を主な目的としている．すなわち，多少変位が犠牲となったとしても，むしろ，より厳密に崩壊荷重を求め，また，各荷重レベルにおける破壊箇所を調べることに重点を置いている．このような考え方に基づいた場合，荷重増分法はRBSMにおける非線形解析法として適した方法の1つであるといえる．RBSMによる反復法や混合法を用いた解析も行われているが，本書ではRBSMによる離散化極限解析でよく利用されている荷重増分法について説明する．荷重増分法における代表的なアルゴリズムとしてはRunge-Kuttaの中点法や，山田の方法，Marcalの方法などがあるが，ここでは山田の方法を取り上げる．
 山田の方法は各荷重増分段階で要素を一つずつ降伏させ，要素を降伏させるために必要な荷重増分量を自動的に定める方法である．この方法は要素数が多く，破壊が進行すると，それに伴い計算時間もかかつてくるが，載荷途中の破壊状況を検討したり崩壊荷重をより厳密に求めるのに適しており，RBSMの特徴や解析目的と良く適合する．
 山田の方法はFEM解析のために開発されているが，RBSMによる離散化極限解析に対しても多少の変更により適用することができる．RBSMによりこの手法を考えた場合，ばねを一つずつすべらせ，それに必要な荷重増分を自動的に決定するといった様に，FEMにおける要素をばねに置き換えて考えればよい．
 ここで，山田の方法を用いた場合の解析の流れを簡単にまとめておく．
 塑性変形を伴う問題において，上記のような解析の流れでは，弾性状態のばねがいつ降伏し塑性状態になるかに重点が置かれている．すなわち，荷重増分率 $r_{\rm min}$ をいかに求めるかという点に特徴がある．
 図3.3はその簡単な説明図である．(n)が前回までの表面力に関する位置で，(n+1)が今回求まった増分表面力 $\boldsymbol{\Delta \sigma}$ を前回までの表面力に加え合わせた位置である．すなわち，今回の増分表面力 $\boldsymbol{\Delta \sigma}$ は $\overline{PR}$ である．$R$ が明らかに初期降伏曲面上の点 $Q$ を越えていれば $\overline{QR}$ という余分な表面力が作用していることになる．そこで，$R$ を $Q$ の位置まで戻し，$\overline{PQ}$ で示される弾性部分のみ取り残すことを考える．
 
図3.3　荷重増分率 $r_{\rm min}$
いま，
\[{\rm (3.19)}   r = \frac{\overline{PQ}}{\overline{PR}} \]
なる荷重増分率 $r$ を計算し，これを増分表面力 $\boldsymbol{\Delta \sigma}$ に掛け合わせた値を前回までの，すなわち，(n)ステップ目における表面力に加え合わせれば余分な表面力を持たないことになる．この $r$ を降伏していないすべてのばねについて計算し，そのうち最小の値を示す $r$ を $r_{\rm min}$ として今回の荷重増分率とする．
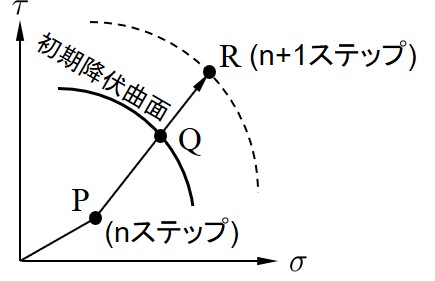
 以上のように，荷重増分率 $r_{\rm min}$ を計算することによって，全荷重の $r_{\rm min}$ 倍の荷重が作用したときの破壊状況を知ることができる． $r_{\rm min}$ は全ばねのうち最小のものから決定されてゆくため，ばねは一つずつ降伏してゆくことになる．なお，全荷重が作用し終わると $r_{\rm min}$ の合計は1となる．
 ここで，$r_{\rm min}$ の別な利用法を考えてみよう．例えば，設計においてある荷重 $P$ を想定していたとしよう．このとき，構造物が $P$ という荷重により崩壊しないように安全率を考慮しているのが普通である．そこで，設計荷重の何倍の荷重が作用したときその構造物が崩壊するかを知つておく必要がある．このような計算では $r_{\rm min}$ が1になっても計算を終了させず，構造物がメカニズムを形成するまで計算する．その結果，得られた荷重増分率 $r_{\rm min}$ の合計は，構造物が破壊するときの設計荷重に対する倍率になる．設計の段階でこの計算を行っておけば，構造物の安全性や経済性のチェックができる．山田の方法をRBSMによる離散化極限解析に適用した場合の各種降伏条件に対する荷重増分率 $r_{\rm min}$ の計算法を以下に示す．
（１）トレス力の条件
 前回までの表面力，すなわち，(n)ステップ目の表面力を $(\sigma_n, \tau)$ とし，新しい荷重増分に対する増分表面力を $(\Delta \sigma_n, \Delta \tau)$としたとき，(n+1)ステップ目の，すなわち，今回の表面力が降伏曲面上にあるためには，以下の式を満足していなければならない．
\[{\rm (3.20)}   ( \tau + r \cdot \Delta \tau)^2 = C^2 \]
ここで，$r$ は荷重増分率であり，今回の増分表面力を $r$ 倍し，前回までの表面力に加え合わせたとき，その全表面力が降伏曲面上にあることを示している．このような計算は，一つの荷重増分の段階で近似的に線形問題として解いているため可能となる．
 式(3.20)を $r$ について整理すると，
\[{\rm (3.21)}   \Delta \tau^2 \cdot r^2 + 2 \tau \cdot \Delta \tau \cdot r + (\tau^2 - C^2) = 0 \]
となる．したがって，$r$ は，2根のうち物理的意味を考慮して次のように求められる．
\[{\rm (3.22)}   r = \frac{-B+\sqrt{B^2 - 4AC}}{2A} \]
ここで，$A$，$B$，$C$ は以下に示す通りである．
\[{\rm (3.23)}   \left. \begin{array}{l} A = \Delta \tau^2 \\ B = 2 \tau \cdot \Delta \tau \\ C = \tau^2 - C^2 \end{array} \right\} \]
（２）ク一口ンの条件
 (1)のトレスカの条件と同様，前回までの表面力を $(\Delta \sigma_n, \Delta \tau)$ とし，今回の荷重増分に対する増分表面力を $(\Delta \sigma_n, \Delta \tau)$ として，表面力が降伏曲面上にある条件を求めると，
\[{\rm (3.24)}   \left( \tau + r \cdot \Delta \tau \right)^2 = \left\{ C - (\sigma_n + r \cdot \Delta \sigma_n) \tan \phi \right\}^2 \]
となる．これを $r$ について整理すると，
\[{\rm (3.25)}   \left\{ \Delta \tau^2 - ( \Delta \sigma_n \tan \phi)^2 \right\} r^2 + 2 \left\{ \tau \cdot \Delta \tau + (C-\sigma_n \tan \phi) \Delta \sigma_n \tan \phi \right\} r \]
\[\hspace{24em} + \left\{ \tau^2 - (C - \sigma_n \tan \phi)^2 \right\} = 0 \]
となる．したがって，$r$ は式(3.22)を解くことによって得られる．ここで，係数$A$，$B$，$C$ はそれぞれ以下の通りである．
\[{\rm (3.26)}   \left. \begin{array}{l} A = \Delta \tau^2 - ( \Delta \sigma_n \tan \phi)^2 \\ B = 2 \left\{ \tau \cdot \Delta \tau + (C-\sigma_n \tan \phi) \Delta \sigma_n \tan \phi \right\} \\ C = \tau^2 - (C - \sigma_n \tan \phi)^2 \end{array} \right\} \]
（３）ミーゼスの条件
 (l)(2)同様，荷重増分率を　$r$ として，
\[{\rm (3.27)}   \frac{1}{4} \left( \sigma_n + r \cdot \Delta \sigma_n \right)^2 + \left( \tau + r \cdot \Delta \tau \right)^2 = C^2 \]
と考えることができる．これを $r$ について整理すると，
\[{\rm (3.28)}   \left( \frac{1}{4} \Delta \sigma_n^2 + \Delta \tau^2 \right) r^2 + \left( \frac{1}{2} \sigma_n \Delta \sigma_n + 2 \tau \cdot \Delta \tau \right) r + \left( \frac{1}{4} \sigma_n^2 + \tau^2 - C^2 \right) = 0 \]
となる．これより，$r$ は式(3.22)を解くことによって求めることができる．ここで，係数$A$，$B$，$C$ は以下の通りである．
\[{\rm (3.29)}   \left. \begin{array}{l} \displaystyle A = \frac{1}{4} \Delta \sigma_n^2 + \Delta \tau^2 \\ \displaystyle B = \frac{1}{2} \sigma_n \Delta \sigma_n + 2 \tau \cdot \Delta \tau \\ \displaystyle C = \frac{1}{4} \sigma_n^2 + \tau^2 - C^2 \end{array} \right\} \]
 上記のように荷重増分率 $r$ を求める計算を，前回の計算で弾性状態もしくは除荷状態にあるすべてのばねについて行い，それらのうち最小の $r$ を今回の荷重増分率 $r_{\rm min}$ とする．RBSMにおける離散化極限解析においては，ここに記していない降伏条件に対しても上記3つの方法と全く同様に合力 $(\sigma_n, \tau)$ によって定式化を行えば荷重増分率を求めることができる．