RBSMでは剛体変位場を仮定している.このため,面内変形要素について考えた場合,$x,y$ 方向の平行変位 $(u,v)$ と剛体回転角 $(\theta)$ の3成分により,各要素の剛体運動を表現することができる.
剛体の自由度を理解するため,
図2.1に示すような長方形をした剛体を考えてみよう.この剛体は面内運動のみ生じ,面外運動は発生しないものとする.このとき,剛体 ABCD が $x$ 方向に並進運動を起こせば,剛体は A'B'C'D' の位置に移動する.ところで,剛体の基本的な特徴は運動が生じても剛体内部における2点間の距離に変化がないことであるから,並進運動が発生した後でも剛体に変形は生じない.同様に回転運動が生じ,$\theta$ だけ回転して剛体が A"B"C"D" となっても形状そのものは元のままである.
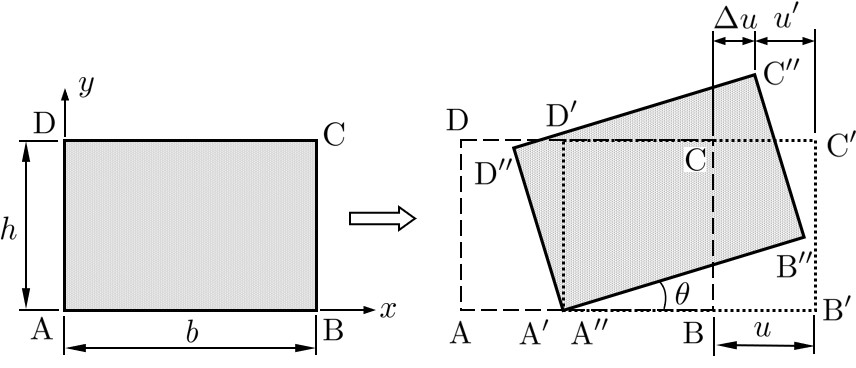
$\hspace{3em}$図2.1 剛体変位場における任意点の移動量
さて,仮にA点に剛体の自由度 $(u, v, \theta)$ を設定したとする.このとき,C点の位置は $x$ 方向への並進運動により C'点へと移動する.さらに,その後,剛体回転を起こせば,C'点は C" 点へと移る.ここで,C 点が C" 点に移動した場合の $x$ 方向の移動量 $\Delta u$ は,
\[
\Delta u = u - u'
\]
と計算することができる.$u$ は並進運動による $x$ 方向の移動量であり,$u'$ は剛体回転によって生じた $x$ 方向の変位成分である.剛体回転角の正方向を反時計回りにとれば,$u'$ は
\[
u'= h \cdot \sin \theta + b \cdot (1-\cos \theta)
\approx h \cdot \theta
\]
となる.ここで,重要なことは,$\sin \theta \approx \theta$,$\left(1-\cos \theta \right) \approx 0$ となるような微小剛体回転角を考えていることである.もし,回転量が大きくなるような場合には,このような近似を行わず有限回転に対する定式化を行う必要がある.
以上から,C点の $x$ 方向移動量 $\Delta u$ は,
\[{\rm (2.1)}
\Delta u = u - h \cdot \theta
\]
と計算できる.同様にして,C点の $y$ 方向移動量を求めると,
\[{\rm (2.2)}
\Delta v = v + b \cdot \theta
\]
となる.
式(2.1)と
式(2.2)の相違点は符号が異なっていること,$h$ の代わりに $b$ となっていることの2点である.
以上の式の展開において,基準点をA点にとったが,要素内変形の生じない剛体変位場では,この点を任意の位置に設定できる.しかし,各々の要素が勝手に基準点を設けているとプログラミング上都合が悪いので,なんらかの法則を設けておいた方が便利である.通常はこの法則として要素の図心を考え,その点に自由度を設定している.以後の展開は特に断わらない限り,図心に自由度 $(u, v, \theta)$ を設けたものとする.
ここで,話をRBSMに戻そう.RBSMにより平面問題の解析を行おうとする場合,FEMと同様,解析領域を有限な領域に分割しなければならない.FEMでは内挿関数に応じて,三角形や四角形などを用いるが,RBSMでは剛体変位場を仮定しているため, 要素形状に何ら制限がない.しかし,一般には計算精度上,凸角形を用いた方がよく,特別な理由がない限り凹角形の使用は避けるべきであろう.話を簡単にするため,また,FEMにおける定ひずみ要素と比較するため,ここでは要素形状を三角形とする.
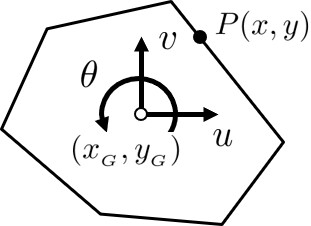
図2.2 面内変形平面要素の自由度
さて,要素図心に平行変位成分 $(u,v)$,及び,剛体回転成分 $(\theta)$ を
図2.2のようにとる.このとき,先の
式(2.1),
式(2.2)と同様,要素境界辺上の任意点 $P$ に関する移動量は図心の剛体変位パラメータにより表すことができる.
いま,図心の座標値を $(x_G, y_G)$ とし,$P$ 点の座標値を $(x,y)$ とすれば,
式(2.1),
式(2.2)における $h$ と $b$ は
図2.2の場合,
\[
h = y - y_{_G} \;,\; b = x - x_{_G}
\]
と考えることができる.したがって,$P$ 点の $x$ 方向, $y$ 方向移動量 $(U,V)$ は,図心の剛体変位により,以下のように表すことができる.
\[{\rm (2.3)}
\left.
\matrix{
U &=& u - (y-y_{_G}) \cdot \theta \cr
V &=& v + (x-x_{_G}) \cdot \theta
}
\right\}
\]
式(2.3)をマトリックスにより表現すれば,以下のようになる。
\[{\rm (2.4)}
\left\{
\matrix{
U \cr
V
}
\right\}
=
\left[
\begin{array}{ccr}
1 & 0 & -(y-y_{_G}) \\
0 & 1 & (x-x_{_G})
\end{array}
\right]
\left\{
\matrix{
u \cr
v \cr
\theta
}
\right\}
\]
RBSMによる面内変形平面間題の解析では,以上のように変位パラメ一夕として,要素図心における剛体変位 $(u, v, \theta)$ の3成分を考えるため,拘束条件を含む系全体の総自由度数は $(要素数) \times 3$となる.定ひずみ要素を用いたFEMにおける全自由度数が節点に依存しているのに対し,異なる点の1つである.
前節ではある一つの要素に着目し,剛体変位場における変位パラメータについて説明した.ここでは,その関係を利用して,2要素間の相対変位について考えてみる.
FEM(変位法)では各要素間に共有節点が存在し,全体剛性行列の重ね合わせはこの節点を基に行われる.一方,RBSMでは要素内に自由度を設けているため,FEMでいうところの節点ではなく,要素図心に設けられた剛体変位により重ね合わせが行われる.しかし,要素内に自由度があるたえめ,要素毎に独立な変位場となり,FEMのような重ね合わせは行えないように思える.
そこで,RBSMでは隣接する2要素間の相対変位を利用し,この相対変位と各要素境界辺上に設けたばねより,各々の要素間に蓄えられるエネルギーを計算することによって各要素間に関連性をもたせ,FEMと同様な重ね合わせを行う.このように,相対変位はRBSMにとって重要な役割を担い,RBSMにおける特徴の一つとなっている.
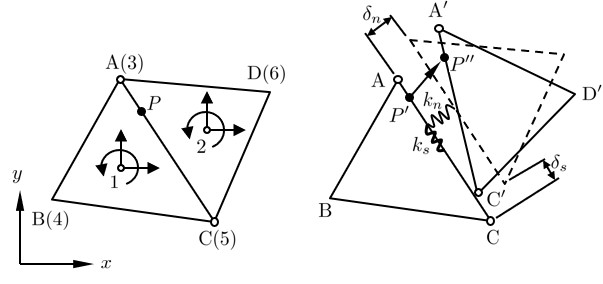
$\hspace{6em}$(a)変形前
$\hspace{8em}$(b)変形後
$\hspace{8em}$図2.3 2要素間の相対変位
さて,2要素間の相対変位を計算するため,
図2.3に示す2枚の剛三角形板を考える.剛三角形板における任意の点 $P(x,y)$ の変位は図心の剛体変位,すなわち,$(u,v,\theta)$ の3成分によって表されることはすでに述べた.これらの剛三角形板がなんらかの外力の作用により,①要素側の $P$ 点が $P'$ 点に,また,②要素側の $P$ 点が $P"$ に移動したとする.このとき,
式(2.4)の関係を使うことで,それぞれの要素における $P$ 点の平行変位 $\boldsymbol{U}=\lfloor U_{\rm I} \; V_{\rm I} \; ; \; U_{\rm II} \; V_{\rm II} \rfloor^t$ が以下のように計算できる.
\[{\rm (2.5)}
\boldsymbol{U}=\boldsymbol{Q \cdot u}
\]
\[\hspace{6em}
\boldsymbol{U}=
\lfloor
U_{\rm I} \; V_{\rm I} \; ; \;
U_{\rm II} \; V_{\rm II}
\rfloor^t
\]
\[\hspace{6em}
\boldsymbol{Q}=
\left[
\begin{array}{c|c}
\begin{array}{ccr}
1 & 0 & -(y-y_{_{G_1}}) \\
0 & 1 & (x-x_{_{G_1}})
\end{array}
& \boldsymbol{0} \\ \hline
\boldsymbol{0} &
\begin{array}{ccr}
1 & 0 & -(y-y_{_{G_2}}) \\
0 & 1 & (x-x_{_{G_2}})
\end{array}
\end{array}
\right]
\]
\[\hspace{6em}
\boldsymbol{u}=
\lfloor
u_1 \; v_1 \; \theta_1 \; ; \;
u_2 \; v_2 \; \theta_2
\rfloor^t
\]
ここで,下付きの添字1,2あるいは ${\rm I,II}$ は,それぞれ,①要素と②要素の物理量であることを,また,${\rm G}$ は図心に関する物理量であることを示している.
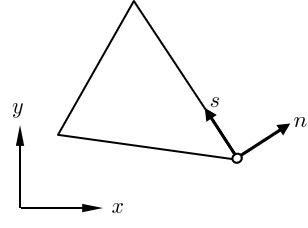
$\hspace{0em}$図2.4 要素境界辺上の局所座標系
式(2.5)における は全体座標系に関する $x$ 方向,$y$ 方向変位であるため,相対変位を計算する上で
図2.4に示すような要素境界辺に沿つた局所座標系に変換しておくと都合がよい.これは,
図2.3からも理解できるように,2要素間の相対変位が要素境界辺に沿つた局所座標系により考えられているためである.いま,座標変換行列を $\boldsymbol{R}$ とし,局所座標系における任意点 $P$ の変位を $\overline{\boldsymbol{U}}$ とすれば,全体座標系における平行変位 $\boldsymbol{U}$ との間に次の関係が成立する.
\[{\rm (2.6)}
\overline{\boldsymbol{U}} = \boldsymbol{R} \cdot \boldsymbol{U}
\]
\[\hspace{6em}
\boldsymbol{R}=
\left[
\begin{array}{c|c}
\begin{array}{ccr}
l_1 & m_1 \\
l_2 & m_2
\end{array}
& \boldsymbol{0} \\ \hline
\boldsymbol{0} &
\begin{array}{ccr}
l_1 & m_1 \\
l_2 & m_2
\end{array}
\end{array}
\right]
\]
\[\hspace{6em}
\begin{array}{rcccl}
l_1 &\!\!\!=\!\!\!& \cos(n,x) &\!\!\!=\!\!\!& y_{35}/l_{35} \\
l_2 &\!\!\!=\!\!\!& \cos(s,x) &\!\!\!=\!\!\!& x_{35}/l_{35} \\
m_1 &\!\!\!=\!\!\!& \cos(n,y) &\!\!\!=\!\!\!& x_{35}/l_{35} \\
m_2 &\!\!\!=\!\!\!& \cos(s,y) &\!\!\!=\!\!\!& y_{35}/l_{35} \\
\end{array}
\]
ここで,$l_1, m_1, l_2, m_2$ は方向余弦であり,$l_{35}$ は
図2.3に示す $\overline{AC}$,すなわち,辺 $\overline{35}$ の長さである.また,$x_{ij}$,$y_{ij}$ は
\[
x_{ij} = x_i - x_j \;,\; y_{ij} = y_i - y_j
\]
であることを意味する.
このようにして,局所座標系における任意点 $P$ の変位 $(\overline{U}, \overline{V})$ が求まれば,2要素間の相対変位は
式(2.7)に示すよう,単純計算によって求めることができる.
\[{\rm (2.7)}
\boldsymbol{\delta} = \boldsymbol{M} \cdot \overline{\boldsymbol{U}}
\]
\[\hspace{5em}
= \left\{
\matrix{
(\overline{P'P''})_n \cr
(\overline{P'P''})_s
}
\right\}
=
\left\{
\matrix{
\delta_n \cr
\delta_s
}
\right\}
=
\left[
\begin{array}{cccc}
-1 & 0 & 1 & 0 \\
0 & -1 & 0 & 1
\end{array}
\right]
\left\{
\matrix{
\overline{U}_{\rm I} \cr
\overline{V}_{\rm I} \cr
\overline{U}_{\rm II} \cr
\overline{V}_{\rm II}
}
\right\}
\]
式(2.7)に
式(2.5),
式(2.6)を代入すれば2要素間の相対変位ベクトル $\boldsymbol{\delta}$ は要素図心の剛体変位 $\boldsymbol{u}$ より以下のように計算することができる.
\[{\rm (2.8)}
\boldsymbol{\delta}
= \boldsymbol{M} \cdot \boldsymbol{R} \cdot \boldsymbol{Q} \cdot \boldsymbol{u}
= \boldsymbol{B} \cdot \boldsymbol{u}
\]
\[\hspace{1em}
\boldsymbol{B}=\boldsymbol{M} \cdot \boldsymbol{R} \cdot \boldsymbol{Q}
\]
\[\hspace{2em}
=
\left[
\begin{array}{c|c|c|c|c|c}
-l_1 & -m_1 & l_1(y-y_{_{G_1}})-m_1(x-x_{_{G_1}}) &
l_1 & m_1 &-l_1(y-y_{_{G_2}})+m_1(x-x_{_{G_2}}) \\
-l_2 & -m_2 & l_2(y-y_{_{G_1}})-m_2(x-x_{_{G_1}}) &
l_2 & m_2 &-l_2(y-y_{_{G_2}})+m_2(x-x_{_{G_2}})
\end{array}
\right]
\]
以上のようにして隣接する2要素間の図心に関する剛体変位と相対変位を関連付けるための $\boldsymbol{B}$ マトリックスを求めることができた.ここで注意をしておきたいことは,$\boldsymbol{B}$ マトリックスが座標値 $(x,y)$ の関数となっていることである.剛性行列を求める際,エネルギー積分を行うが,この場合にこの座標値が積分に影響を与える.詳細については剛性行列作成の節で説明する.
RBSMでは隣接する2要素間にばねを設定し,そのばねを通して力が伝わるものと考えている.ばねとしては,面内変形平面要素の場合,
図2.5に示すように垂直方向の相対変位 $\delta_n$ に抵抗するばね $k_n$ と,せん断方向のずれに対応する相対変位 $\delta_s$ に抵抗するばね $k_s$ の2種類を考える.
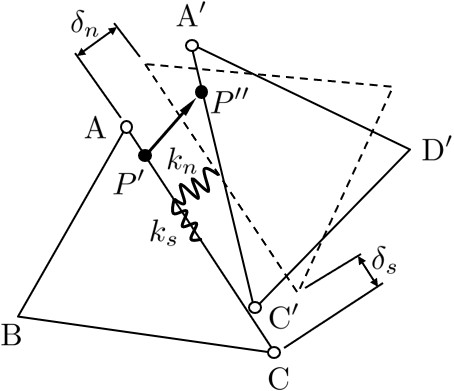
$\hspace{2em}$図2.5 2要素間の分布ばね $(k_n,k_s)$
ばね系の力学では力と変位が
\[
P = k \cdot \delta
\]
なる関係を持つていることは良く知られていることであるが,RBSMでも同様に相対変位 $(\delta_n, \delta_s)$ と単位面積当りの表面力との間に以下の関係が成立しているものと仮定する.
\[{\rm (2.9)}
\left.
\matrix{
\sigma_n &\!\!\!\!\!= k_n \cdot \delta_n \cr
\tau &\!\!\!\!\!= k_s \cdot \delta_s
}
\right\}
\]
ここで,$(\sigma_n,\tau)$ は,それぞれ,垂直とせん断方向における単位面積当りの表面力である.FEM(変位法)では,通常,要素内応力を考えているが,この応力はテンソル量として扱われる.しかし,RBSMでは,
式(2.9)のように単位面積当りの表面力をベクトル量として扱う.このため,材料非線形問題に対する構成式の取り扱い方がFEMとRBSMとでは多少異なつてくる.このような非線形問題に対する構成式の取り扱い方については次章において説明する.
後の式の展開のため,
式(2.9)を行列で以下のように表しておく.
\[{\rm (2.10)}
\boldsymbol{\sigma} = \boldsymbol{D \cdot \delta}
\]
\[\hspace{5em}
\boldsymbol{\sigma} = \lfloor \sigma_n , \tau \rfloor^t
\;,\;
\boldsymbol{D} =
\left[
\matrix{
k_n & 0 \cr
0 & k_s
}
\right]
\;,\;
\boldsymbol{\delta} = \lfloor \delta_n , \delta_s \rfloor^t
\]
さて,
式(2.10)におけるばね定数 を決定するに当り,相対変位成分に対応する仮想ひずみ成分を仮定する.ここで,仮想ひずみ成分とことわったのは,FEMで扱うひずみがテンソル量であるのに対し,RBSMでのそれは単に,単位長さ当りの相対変位という意味であり,それを強調したいためである.
図心間の垂線を基準に単位長さ当たりの相対変位を考えた場合,仮想ひずみ成分は垂直方向を $\varepsilon_n$,せん断方向を $\gamma_s$ として,
\[{\rm (2.11)}
\boldsymbol{\varepsilon}
=
\left\{
\matrix{
\varepsilon_n \cr
\gamma_s
}
\right\}
=
\frac{1}{h_1+h_2}
\left\{
\matrix{
\delta_n \cr
\delta_s
}
\right\}
=
\frac{1}{h}
\boldsymbol{\delta}
\]
と表すことができる.ここで,$h=h_1+h_2$ であり,$h_1, h_2$ は
図2.6に示されているように,それぞれ,三角形要素の図心 $(x_G, y_G)$ から要素境界辺上に下した垂線の高さを表している.この垂線の高さを基礎として相対変位に関する仮想ひずみ成分を定義することに対しては,いまだ議論の余地が残されている.
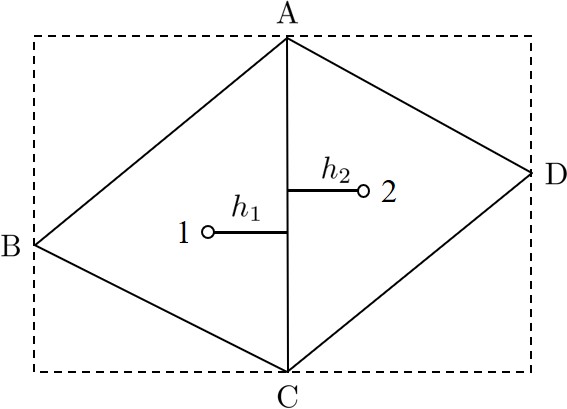
$\hspace{4em}$図2.6 垂線の定義
次に,一軸状態を想定し,各要素境界辺上における単位面積当りの表面力を仮定する.弾性係数を $E$,ポアソン比を $\nu$ として,平面ひずみ状態及び平面応力状態を考えると,以下のように応力とひずみの関係が得られる.
(平面ひずみ状態)
\[{\rm (2.12)}
\left.
\begin{array}{rl}
\sigma_n &
\displaystyle \!\!\!\!\!
= \frac{(1-\nu)E}{(1-2 \nu)(1+\nu)} \varepsilon_n \\[1em]
\tau &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu} \gamma_s
\end{array}
\right\}
\]
(平面応力状態)
\[{\rm (2.13)}
\left.
\begin{array}{rl}
\sigma_n &
\displaystyle \!\!\!\!\!
= \frac{E}{(1- \nu^2)} \varepsilon_n \\[1em]
\tau &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu} \gamma_s
\end{array}
\right\}
\]
以上の関係から,平面ひずみ状態及び平面応力状態のばね定数が以下のように決定される.
(1)平面ひずみ状態のばね定数
式(2.12)に
式(2.11)を代入し,整理すると,
\[{\rm (2.14)}
\left.
\begin{array}{rl}
\sigma_n &
\displaystyle \!\!\!\!\!
= \frac{(1-\nu)E}{(1-2 \nu)(1+\nu)}
\cdot \frac{\delta_n}{h_1+h_2} \\[1em]
\tau &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{\delta_s}{h_1+h_2}
\end{array}
\right\}
\]
となる.ここで,
式(2.14)と
式(2.9)を比較することにより相対変位と単位面積当りの表面力を結び付けるばね定数 $(k_n,k_s)$ が以下のように得られる.
\[{\rm (2.15)}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{(1-\nu)E}{(1-2 \nu)(1+\nu)}
\cdot \frac{1}{h_1+h_2} \\[1em]
k_s &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{1}{h_1+h_2}
\end{array}
\right\}
\]
(2)平面応力状態のばね定数
平面ひずみ状態と同様,
式(2.13)に
式(2.11)を代入し,整理すると,
\[{\rm (2.16)}
\left.
\begin{array}{rl}
\sigma_n &
\displaystyle \!\!\!\!\!
= \frac{E}{(1- \nu^2)}
\cdot \frac{\delta_n}{h_1+h_2} \\[1em]
\tau &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{\delta_s}{h_1+h_2} \\[1em]
\end{array}
\right\}
\]
となる.ここで,先と同様,
式(2.16)と
式(2.9)を比較することにより,ばね定数 $(k_n,k_s)$ が以下のように得られる.
\[{\rm (2.17)}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{E}{(1- \nu^2)}
\cdot \frac{1}{h_1+h_2} \\[1em]
k_s &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{1}{h_1+h_2} \\[1em]
\end{array}
\right\}
\]
このようにしてばね定数を一義的に決定してきたが,この方法は便宜上の方法であり他に幾つかの方法が考えられる.例えば,実験,実測などのデータから推定するのもその一つの方法であろう.特に,岩盤などに見られる断層面の評価を行う場合は実測から推定した方がよい.
本来,RBSM は極限解析用のモデルであり,崩壊荷重や破壊パ夕一ンを求めることを目的としているため,弾性解析には適していない.構造物が崩壊する荷重値の近傍では,むしろ弾性的なひずみより剛体的な移動のほうが卓越するものと思われるため,弾性時の挙動を多少犠牲にしてもよいのであれば,先の近似は十分な精度を持つてるものと見なせる.
これまで述べてきた結果を利用して,RBSMにおける要素剛性行列を導くことにする.ただし,要素といってもいわゆるFEMにおける要素と異なり,隣接する2要素間の境界辺に対して剛性行列が導かれる.すなわち,要素境界辺上に分布しているばねを要素と考え,ここに蓄えられるエネルギーを評価することによって剛性行列を求める.このような理由により,FEMにおける要素剛性行列と区別するため,ここではこの剛性行列をばね剛性行列と呼ぶ.
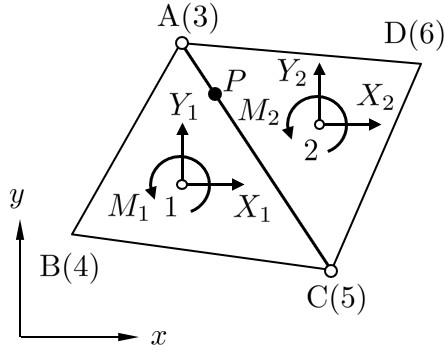
$\hspace{1em}$図2.7 要素図心の節点外力
ばね剛性行列を導くに当り,代表的な2つの剛三角形板に挟まれた要素境界辺 を取り出す.この要素は
図2.7に示すよう要素図心に作用する外力 $\boldsymbol{F}$ に対し,つり合い状態にある.このとき,各図心に関する仮想剛体変位を $\boldsymbol{u}^*$ とすれば,外力の成す仮想仕事は以下のようになる.
\[{\rm (2.18)}
W_o = {}^t\boldsymbol{u}^* \cdot \boldsymbol{F}
\]
\[\hspace{6em}
\boldsymbol{u}^*
=
\lfloor
u_1^* \; v_1^* \; \theta_1^* \;;\;
u_2^* \; v_2^* \; \theta_2^*
\rfloor^t
\]
\[\hspace{6em}
\boldsymbol{F}
=
\lfloor
X_1 \; Y_1 \; M_1 \;;\;
X_2 \; Y_2 \; M_2
\rfloor^t
\]
一方,要素境界辺上の表面力の成す仮想仕事は,
式(2.8),
式(2.10)を用い,仮想相対変位を $\boldsymbol{\delta}^*$ として
\[{\rm (2.19)}
W_I = \int{}^t \boldsymbol{\delta}^* \cdot \boldsymbol{\sigma} ds
= \int{}^t \boldsymbol{\delta}^* \cdot\boldsymbol{D \cdot \delta} ds
\]
\[\hspace{6.5em}
= {}^t \boldsymbol{u}^*
\int \left( \boldsymbol{B}^t \boldsymbol{\cdot D \cdot B} \right) ds
\boldsymbol{u}
\]
\[\hspace{7em}
\left( \because \boldsymbol{\delta}^* = \boldsymbol{B \cdot u}^* \right)
\]
と表すことができる.仮想仕事の原理は外力の成す仮想仕事と内力の成す仮想仕事が等しいということであるから,
式(2.18)及び
式(2.19)より以下の関係が得られる.
\[{\rm (2.20)}
W_o = W_I
\]
\[\hspace{6em}
{}^t\boldsymbol{u}^* \cdot \boldsymbol{F}
=
{}^t \boldsymbol{u}^*
\int \left( \boldsymbol{B}^t \boldsymbol{\cdot D \cdot B} \right) ds
\boldsymbol{u}
\]
ここで,仮想変位 $\boldsymbol{u}^*$ は任意であるから,最終的に
式(2.20)は次式のごとく変形される.
\[{\rm (2.21)}
\boldsymbol{F}
=
\int \left( \boldsymbol{B}^t \boldsymbol{\cdot D \cdot B} \right) ds
\boldsymbol{u}
=
\boldsymbol{K \cdot u}
\]
結局,
式(2.21)における $\boldsymbol{K}$ がばね剛性行列となる.この行列のサイズは(6×6)となり,FEMにおける定ひずみ要素の剛性行列と同じサイズとなっている.
ところで,$\boldsymbol{B}$ マトリックスは座標の関数となっているため,ばね剛性行列を陽な形式で表現しておくためには線積分(2次元問題の場合)を行わなければならない.線積分については
7章にゆずり,ここでは,その結果のみ記す.
\[{\rm (2.22)}
\boldsymbol{K}
=
\left[
\begin{array}{cccccc}
K_{11} & K_{12} & K_{13} & K_{14} & K_{15} & K_{16} \\
& K_{22} & K_{23} & K_{24} & K_{25} & K_{26} \\
& & K_{33} & K_{34} & K_{35} & K_{36} \\
& & & K_{44} & K_{45} & K_{46} \\
&{\rm sym.}& & & K_{55} & K_{56} \\
& & & & & K_{66}
\end{array}
\right]
\]
\[
\left\{
\begin{array}{l}
K_{11} = k_n y_{35}^2 + k_s x_{35}^2 \\
K_{12} = -(k_n-k_s) y_{35}x_{35} \\
K_{13} = -k_ny_{35} \Delta_{11} + k_s x_{35}\Delta_{21} \\
K_{14} = -K_{11} \\
K_{15} = -K_{12} \\
K_{16} = -k_ny_{35} \Delta_{22} + k_s x_{35}\Delta_{12}
\end{array}
\right.
\hspace{3em}
\left\{
\begin{array}{l}
K_{22} = k_n x_{35}^2 + k_s y_{35}^2 \\
K_{23} = k_nx_{35} \Delta_{11} + k_s y_{35}\Delta_{21} \\
K_{24} = -K_{12} \\
K_{25} = -K_{22} \\
K_{26} = k_nx_{35} \Delta_{22} + k_s y_{35}\Delta_{12}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{33} = k_n \Delta_{11}^2 + k_s \Delta_{21}^2 + k_n l_{35}^4/12\\
K_{34} = -K_{13} \\
K_{35} = -K_{23} \\
K_{36} = k_n \Delta_{11} \Delta_{22}
+ k_s \Delta_{21} \Delta_{12}
- k_n l_{35}^4/12
\end{array}
\right.
\hspace{3em}
\left\{
\begin{array}{l}
K_{44} = K_{11} \\
K_{45} = K_{12} \\
K_{46} =-K_{16}
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
K_{55} = K_{22} \\
K_{56} =-K_{26}
\end{array}
\right.
\hspace{3em}
K_{66} = k_n \Delta_{22}^2
+ k_s \Delta_{12}^2
+ k_n l_{35}^4/12
\hspace{4em}
\left( \times 1/l_{35} \right)
\]
\[
\left\{
\begin{array}{l}
2 \Delta_{11} = x_{35}(x_{31}+x_{51})
+ y_{35}(y_{31}+y_{51}) \\
2 \Delta_{12} = x_{35}(y_{32}+y_{52})
- y_{35}(x_{32}+x_{52}) \\
2 \Delta_{21} =-x_{35}(y_{31}+y_{51})
+ y_{35}(x_{31}+x_{51}) \\
2 \Delta_{22} =-x_{35}(x_{32}+x_{52})
- y_{35}(y_{32}+y_{52})
\end{array}
\right.
\]
\[\hspace{2em}
\left( x_{ij} = x_i - x_j , y_{ij} = y_i - y_j \right)
\]
このようにして作成されたばね剛性行列をもとに全体剛性行列を組み立てる.重ね合わせの手順としては要素図心の剛体変位 $(u,v,\theta)$ をパラメータとして行えばよい.FEMに精通している読者は,FEMにおける要素をRBSMの要素境界辺に,また,FEMでいうところの節点変位を要素図心の剛体変位に置きなおして考えればよい.
FEMにおける定ひずみ要素では,要素構成節点数が3で,各節点における自由度が2であるのに対し,RBSMではばね構成要素数が2(各要素境界辺に関係する要素が2であることを意味する)で,各要素の自由度が3である.このように考えれば,全体剛性行列の作成はFEMの場合と何等変わるところがなく,アルゴリズム的にはFEMの場合と同様となる.
さらに,得られた全体剛性行列を解く手法はFEMにおける連立方程式解析のためのライブラリがそのまま利用できる.
前節では剛性行列の作成法について述べた.実際にこの連立方程式を解いて要素図心の剛体変位を求めるためには支点条件の導入,及び荷重条件の処理を行わなければならない.ここでは,支点条件の処理方法について述べる.
FEMでは,節点毎に変位に関する自由度を設定するため,通常,
図2.8に示すような変位境界条件を用いる.
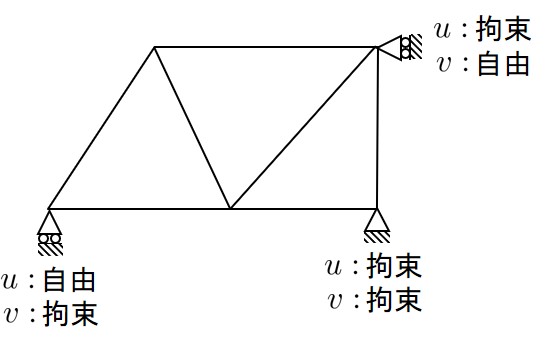
$\hspace{1em}$図2.8 FEMにおける拘束条件
一方,RBSMでは,変位自由度として $(u,v,\theta)$ の3自由度を考えるため,剛体回転角 $(\theta)$ についても何等かの拘束条件を与える必要がある.このことは,変形法を用いた骨組構造解析を思い起こせば理解できるであろう.また,自由度の位置が要素図心に設けられていることもFEMの場合と大きく異なる点の一つである.しかも,要素を剛体としているため,
図2.9(a)のようなケースにおいて
図2.9(b)のように①要素を固定すると図のように本来のモデルと異なった構造になる.
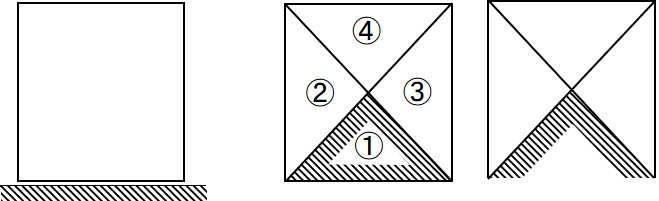
$\hspace{1em}$(a) 本来のモデル
$\hspace{4em}$(b) 誤つた拘束条件
$\hspace{6em}$図2.9 誤つた拘束条件の処理
このような点に着目して開発されたのが境界用の要素である.いま,
図2.9と同様なモデルを考え,拘束したい位置に
図2.10に示す①のような要素を考える.この要素は3番目の節点が存在せず,当然,質量も面積も持たない.自由度のみ三角形(2-1-0)の図心,すなわち,辺 $\overline{21}$ の中点に存在する.このような状態で,①要素を拘束すれば,実際のモデルにより近い状態となる.
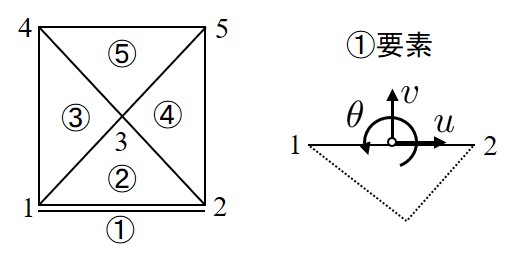
$\hspace{4em}$図2.10 RBSMの境界用要素
それでは,①②要素間の境界辺におけるばね剛性行列を作成する場合にはどのようにしたらよいであろうか.このような場合には,
図2.11に示すように,境界用の要素①の垂線 $h_1$ を単純に0と仮定し,前節で得られた剛性行列をそのまま利用すればよい.
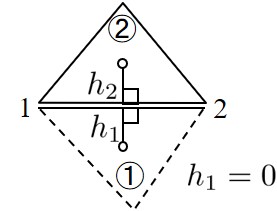
$\hspace{1em}$図2.11 境界用要素の垂線
このように考えれば,特別な剛性行列を用意する必要がなく,プログラミングも簡単になる.ただし,有限要素法のよう,ある節点のみを固定することはできず,
図2.12に示すような,構造物に対し剛板を添えた状態となる.

図2.12 RBSMの境界条件
以上のようにして境界用の要素自由度に拘束条件を果たすことにより種々の境界条件を処理すれば,その後の全体剛性行列に対する支点条件の処理は,FEMの場合と同様な扱いとなる.
以下に拘束条件の種類を示しておく.
① 自由 固定 固定
② 自由 固定 自由
③ 固定 自由 固定
④ 固定 自由 自由
⑤ 固定 固定 固定
⑥ 固定 固定 自由
ここで,$(u,v)$ はそれぞれ,$x$ 方向及び $y$ 方向の平行変位であり,$(\theta)$ は剛体回転角である.$x$ 方向に対して対称条件を用いるなら③の条件を,また,$y$ 方向に対して対称条件を用いるなら①の条件を用いればよい.
このように,RBSMでは節点を拘束したい場合に多少の不便を伴う.そこで,次に節点を拘束したい場合の処理について説明する.もともと,RBSMでは剛体変位場を仮定しているため,要素の図心に自由度を置く必要性は全くない.プログラミング上の簡便さから図心位置に設定したにすぎないため,その考え方を変えて別の位置に自由度を持つてきても差し支えない.そこで,
図2.13に示すよう,境界用の要素に関する自由度を拘束したい側に移動する.図は節点1側に移動した例である.もし,$x$ 方向自由,$y$ 方向拘束としたければ,
② 自由 固定 自由
とする.ここで注意をしなければならないことは,剛体回転角 $(\theta)$ を固定してはならないことである.もし, $(\theta)$ を固定してしまえば境界用の要素は回転できなくなり,先の図心に関する境界条件①と同じ結果となってしまう.このように,節点に対して拘束条件を考える場合は常に剛体回転角 $(\theta)$ は自由としておかなければならない.
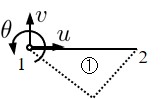
図2.13 境界用要素の自由度の移動
最後に斜め境界について考えてみよう.有限要素法では
図2.14(a)に示すよう,全体座標系 $(x-y)$ に対し,局所座標系 $(\overline{x}-\overline{y})$ を考え,対応する剛性行列における自由度設定位置に座標変換を施す.その結果に対して拘束条件を導入すれば斜め境界を扱える.
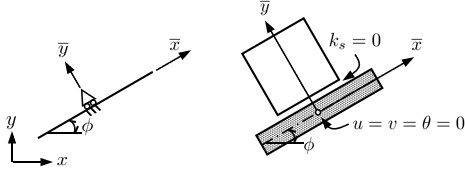
$\hspace{5em}$(a) FEM
$\hspace{7em}$(b) RBSM
$\hspace{6em}$図2.14 斜め境界の処理
RBSMでも同様な手法を用いることもできるが,さらに簡単に処理することもできる.もともと,RBSMでは要素境界辺上に沿つた座標系を考え,相対変位とばねから表面力を計算しているため,
図2.14(b)のように境界用要素の自由度を拘束し,せん断に抵抗するばねを $k_s=0$ とする.このように設定するとせん断方向に抵抗するものがなくなるため,これに沿つた方向の変位は目由になり,剛板上の要素はそれに沿つてスライドする.これは,$\overline{x}$ 方向に対して自由,$\overline{y}$ 方向に対して拘束した状態と同じである.すなわち,$k_s=0$ とすることで自動的に斜め境界を導入したことになる.煩わしい座標変換も無く,プログラミングも簡単になる.
境界用の要素を用いる利点はもう一つある.それは,無限領域を扱う場合,境界要素法の考え方をそのままRBSMの境界要素に適用できることである.この点に関しては今後の成果に期待したいところである.
地盤の内部は種類の異なる材料が層状になり,複雑な様相を成している.また,鋼構造物においても板厚の異なる材料が接合されているなど,異なった種類の要素が隣接することも多々ある.これらの問題を解析しようとする場合,FEMと同様,RBSMにおいても,その材料定数の変わり目で要素分割を行つておく必要がある.ここでは,このような材料の種類が2要素間で異なる場合の処理について述べる.
さて,RBSMでは隣接する2要素間の境界辺上にばねを設け,そのばねを通して力が伝わるものと考える.したがって,隣接する要素が同一材料で,同じ板厚なら問題はないのだが,これらが異なっていた場合,どちらの材料あるいは板厚によりばね定数と強度定数を設定するか検討しなければならない.強度定数については弱い方の定数を用いるという考え方もできるが,ばね定数については必ずしもこのような方法が良いとは限らない.
図2.15に示すような板厚が異なる場合も同様である.
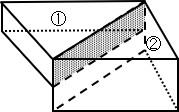
図2.15 板厚が異なる2要素が隣接した場合
このような問題に対処する第1の方法は,隣接する2要素の材料定数に関する平均値を利用することである.平均値といっても単純平均ではなく,隣接する三角形の各垂線を重みとして考えた方がより良い.例えば①要素の垂線 $h_1$,②要素の垂線 $h_2$ とし,問題としている材料定数を,それぞれ,$E_1$,$E_2$ としたとき,その材料定数の平均値 $E_{\rm mean}$ を
\[{\rm (2.23)}
E_{\rm mean}
=
\frac{h_1 E_1 + h_2 E_2}{h_1+h_2}
\]
として求める.この方法は変形に係わる定数,例えば弾性係数やポアソン比などについては良い近似を与えるものと思われるが,強度定数に用いた場合,極端に悪い結果となる場合もある.
図2.16はそのよい例であろう.
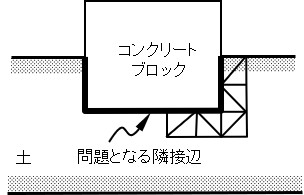
図2.16 材料定数の異なる隣接辺
コンクリートと土の強度とではオーダー的にも大きく異なるため,平均値を採用すれば中間値程度の強度となり,実際の現象とは異なってしまう.もし,強度が明らかに大きいか小さいか判明していれば,変形に関係する材料定数については平均値を,強度に係わる材料定数については弱い方を採用するといった方法も考えられる.しかし,破壊条件の違いにより,強度の大小が応力状態によって変わる場合などはそのときの状態によって異なる.
第2の方法は,材料の異なる要素境界辺に前節で説明した境界用の要素を用いることである.この境界用の要素には材料定数を与えず,
図2.17に示すよう,①要素側については①要素の材料定数を,また,②要素側については②要素の材料定数を用いる.このようにすれば,多少自由度は増えるものの,応力状態を意識せずに破壊条件を導入することができる.ただし,この場合注意しなければならないことは,境界用要素に関する構成節点番号の考え方である.
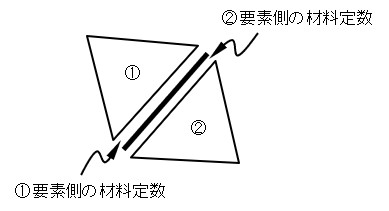
図2.17 異なる材料定数処理のための境界用要素
①要素側から見た場合,境界用要素の構成節点番号は
図2.18に示すように4→3となるし,②要素側から見た場合,3→4となる.もし,この区別を行わなかった場合,法線方向の定義がばらばらとなり,本来,同じ応力状態になければならないにもかかわらず,大きさは同じであるが,符号の異なった応力値が得られる.応力の符号が異なれば,当然,非線形解析を行った場合不都合が生じる.これを避ける方法は,法線方向の決定に際し,①要素から③要素に,また,②要素から③要素に向かうよう考え,ばねの構成節点番号を①要素あるいは②要素の要素構成節点番号から決めればよい.このように考えれば,常に反時計回りの方向にばね構成節点番号が決定され,統一性が保たれる.
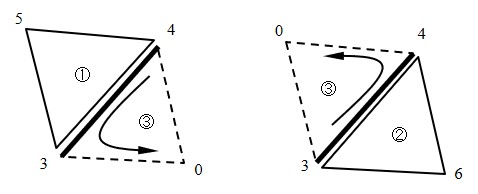
$\hspace{2em}$(a) ①要素側
$\hspace{6em}$(b) ②要素側
$\hspace{6em}$図2.18 斜め境界の処理
第2の方法はよい近似を与える一方で,多少プログラムが複雜になる傾向にある.そこで,第3の方法として,材料の異なる要素境界辺上のばね定数を直接入力することが考えられる.定数の直接入力であるから,値としては何を入力してもかまわないため,変形にかかわる定数については平均値を,また,強度関係の定数については支配的な値を入力するということもできる.
材料定数が徐々に変化するようなケースでは第1の平均値を用いる方法を,また,板厚が異なるようなケースでは第2の方法を,合成構造の継ぎ目や岩盤などの断層面では第3の方法を用いるとよい.いずれにせよ,解析する問題に応じて選択すべきであろう.
RBSMの自由度設定位置は便宣上要素図心にとっている.荷重も自由度と同じ位置に載荷することが原則である.
図2.19は要素図心に載荷された $x$ 方向荷重 $X$,$y$ 方向荷重 $Y$,モーメント荷重 $M$ を示したものである.FEMと異なる点は $x$,$y$ 方向荷重の他,モーメント荷重が存在していることである.モーメント荷重を使用するケースは少ないが,後で若干の説明を行う.
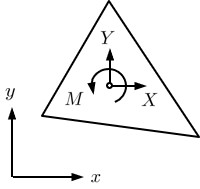
図2.19 要素図心に作用する外力
さて,
図2.20(a)に示すよう,等分布荷重が作用した場合について考えてみよう.FEMでは分布荷重を
図2.20(b)に示すよう,等価節点外力に置き直して考える.一方,RBSMでは要素図心に外力が作用するため,FEMのように節点に外力を与えることはできない.そこで,
図2.20(c)に示すよう,境界用要素を導入し,その要素の図心に外力を与える.このようにすると,要素境界辺上に分布ばねがあるため,境界用要素①から辺 $\overline{12}$ 上に分布したばねを通して②要素に伝わる.①要素も剛体運動を起こすため,①要素の図心に与えた集中荷重は辺 $\overline{12}$ 上に分布して作用した場合と同じ結果となり,
図2.20(a)のモデルを再現できる.
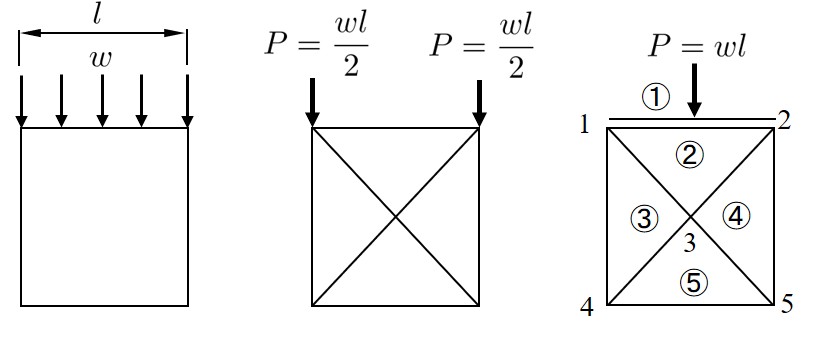
$\hspace{1em}$(a) モデル
$\hspace{6em}$(b) FEM
$\hspace{6em}$(c) RBSM
$\hspace{8em}$図2.20 等分布荷重の処理
また,
図2.21(a)に示すよう,台形分布荷重が作用した場合どうであろうか.この場合は荷重を
図2.21(b)のように分解して考えると理解しやすい.
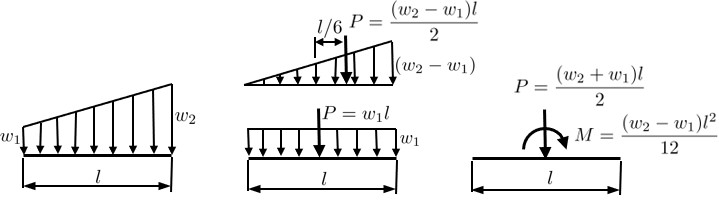
$\hspace{2em}$(a) モデル
$\hspace{5em}$(b) 荷重の分解
$\hspace{3em}$(c) 等価外力
$\hspace{8em}$図2.21 台形分布荷重の処理
台形分布荷重による鉛直方向の全荷重は以下のように計算できる.
\[
P = \frac{w_1 + w_2}{2} \cdot l
\]
しかし,合力が境界用要素の図心,すなわち,辺 $\overline{12}$ の中点ではなく偏心して作用する.この偏心による効果をRBSMでは以下のようにモーメント荷重として取り込む.
\[
M = \frac{w_1 - w_2}{12} \cdot l^2
\]
以上のように等価外力を考え,
図2.21(c)に示すような集中荷重を境界用要素図心に作用させる.このようにすると等分布荷重の場合と同様,辺 $\overline{12}$ に分布したばねを通して台形分布荷重を作用させることができる.
一方,集中荷重の場合はどうであろうか.FEMでは節点上に荷重を作用させるため,分布荷重と比べ簡単に処理できる.しかし,RBSMでは要素図心に自由度があるため,簡単に集中荷重を扱うことはできない.このような問題に対処するため,支点条件のところで説明したように,境界用要素の図心位置を
図2.22(a)に示すよう移動する方法が考えられが,このように処理した場合においても境界用要素が剛体であるため,集中荷重 は辺 $\overline{12}$ 上に分布する.
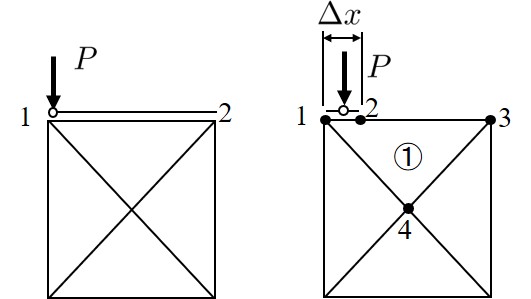
$\hspace{0em}$(a) 図心をずらした場合
$\hspace{1em}$(b) 微小境界用要素を用いた場合
$\hspace{6em}$図2.22 集中荷重の処理
そこで,
図2.22(b)に示すような微小境界用要素を考え,その要素に集中荷重を作用させる.この場合,辺 $\overline{12}$ 上に集中荷重は分布するが,境界辺 $\overline{12}$ の長さ $\Delta x$ を微小にとれば,近似的に集中荷重を取り扱うことができる.このとき,要素①の形状は三角形であるが,その構成節点数は(1-4-3- 2)のごとく4節点となることに注意しなければならない.RBSMでは剛体変位場を仮定しており,原則的には任意多角形を用いることができるため,前記のような考え方も可能となるのである.
地盤解析などでは頻繁に物体力を扱う場合が現れるが,次に,この物体力について考えてみる.FEMでは,要素内に作用する物体力を等価節点力に置き直し要素構成節点に振り分けるが,RBSMではもともと図心に外力が作用するため,要素面積に単位体積重量を掛け合わせ,得られた集中荷重を外力として要素図心に作用させればよい.
以上述べたように,RBSMは分布荷重や物体力に対しては取り扱いが簡単であるが,集中荷重の場合は多少面倒になる.しかし,実際の載荷試験などの状態を考えたとき,先に述べた近似的集中荷重による方法でも,取り扱い方さえ注意すれば実務上差し支えない程度に使用することができる.





















