1.散化極限解析の概要
1-1 極限解析とRBSM
鋼構造物,鉄筋コンクリート構造物,基礎構造物などに代表されるあらゆる構造物を構築する場合,安全性を確保することは必ず達成しなくてはならない目標の一つである.もちろん,安全性と同時に経済性も無視することはできない.いくら安全性の高い丈夫な構造物を作つたとしても,採算性がなければその構造物が建造される可能性は少ないであろうし,また,経費を節約したがために,壊れやすい構造物になってしまったのでは現実的ではない.採算性には金銭的なことも含まれるであろうし,公共性などの利用価値的な金額には現れないようなことも含まれる.このような場合には,どのような荷重状態まで安全性を確保するかといった,安全性の程度までが問題となつてくるため,総合的な意味で経済性や安全性の両者を満足させることは決してたやすいことではない.
安全性とは何を基準に考えたらよいのであろうか.一つには,構造物に重大な変形や塑性が発生しないよう,応力に対して安全率を考えることができよう.このような考え方に対する代表的な方法として,許容応力度設計法がある.しかし,鋼材などのように,ある荷重状態までは弾性と見なすことができるような特性を持つ材料なら比較的に考えやすいが,土や岩盤などのように,初めから非線形挙動を示す材料では許容応力度設計法を適用しにくいこともある.そこで,もう一つの方法として,構造物が崩壊するような荷重値に対し設計荷重にどれくらい余裕を持たせるかといった考え方が生まれてくる.すなわち,構造物の限界状態を知り,それから逆算して安全性を検討する方法である.このような設計法には
いずれにせよ,構造物を設計する上で,どの程度の荷重でその構造物が壊れるのか,また,壊れるとしたらどのような崩壊形式を示すのか,それらを理解しておくことは重要なことである.このような現象を理解するために適している手法の一つとして
従来の極限解析法を利用し,構造物を
このような極限解析に対する離散化解析法の一つとして
いま,RBSMを理解するため,
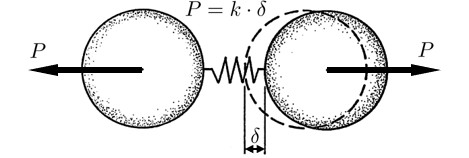
RBSMでは,上記の理由から要素内応力を考えていないが,崩壊機構条件と要素境界面上の表面力に関するつり合条件を満足しているため, 崩壊荷重に対する
RBSMを用いた極限解析用のプログラムを理解し,作成する上で,極限解析手法に関する知識が無くても差し支えないが,基礎的な知識を持っていればより本質的な理解ができる.
1-2 RBSMと有限要素法
航空機構造技術者によって開発され,電子計算機の発達に伴つて驚異的進歩を遂げた本書は,RBSMのプログラミングを理解するためのものであるため,FEM自身については触れず,FEMを理解している読者のために,FEMにおいて最も簡単な
| 項目 | FEM | RBSM |
|---|---|---|
| 要素形状 | 三角形 | 任意多角形 |
| 自由度設定位置 | 三角形の頂点 | 要素内の任意点 (便宜上,図心点にとる) |
| 自由度 | 各節点において$(x,y)$方向の平行変位,2自由度 | 剛体運動を規定する$(x,y)$方向の平行変位と剛体回転の3自由度 |
| 要素剛性行列のサイズ | 要素毎に作成 $(6 \times 6)$ |
要素境界辺毎に作成$(6 \times 6)$ |
| 応力 | 要素内応力 (テンソル量) |
要素境界辺上の表面力 (ベクトル量) |
FEMでは,解析領域を有限な要素(定ひずみ要素の場合は三角形要素)に分割する. 一方,RBSMにおいても,FEMと同様,要素に分割しなければならない. この観点からすると,RBSMもFEMも同じ領域型解法の一つといえる. ただし,RBSMでは要素内変形を無視し,各要素境界辺上の表面力に関するつり合いを考えているため, 要素分割形状をどのように行つても原則的にはかまわない.

$\hspace{5em}$
FEM における定ひずみ要素の場合,
$\hspace{6em}$
しかし,各要素の自由度設定位置がまちまちに設けられていたのではプログラミング上都合が悪いため,通常は
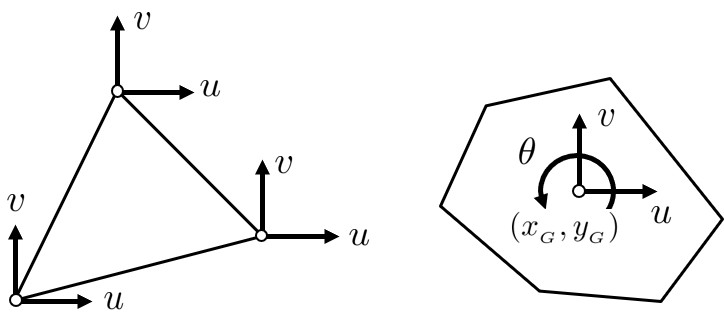
FEMの定ひずみ要素では三角形の各頂点に自由度を設定し,各々の節点に 方向の平行変位 $(u,v)$ の2自由度を考える.
一方,RBSMでは,剛体運動を規定する $x, y$ 方向の
FEMの定ひずみ要素では三角形の各頂点に $x,y$ 方向の変位自由度 $(u,v)$ を設定しているため,要素毎に, 2(各節点の自由度数)× 3(要素構成節点数)= 6 の自由度が存在する.したがって,要素剛性行列のサイズは(6×6)となる.
一方,RBSMは,2つの剛板を垂直方向とせん断方向に抵抗する2種類のばねにより結合し,このばねに蓄えられるエネルギーから要素剛性行列を求める.いま,各要素の自由度が3であり,ばねに関係する要素数が2であるため要素境界辺毎,すなわち,各ばねに対して, 3(要素図心の自由度数)× 2(ばね構成要素数)= 6 の自由度が設定される.このことから,要素剛性行列のサイズは(6×6)となり,FEMの定ひずみ要素と同じ行列サイズとなる.
FEMにおける定ひずみ要素では,
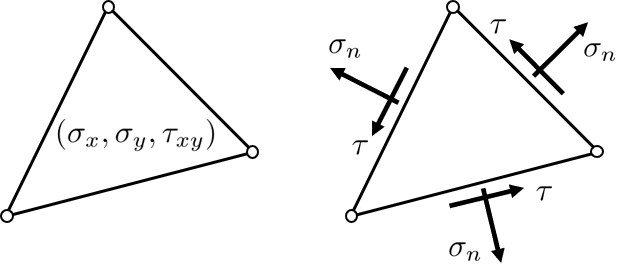
$\hspace{7em}$