5.離散化解析の変位計算
- 5-1 プログラム構造
- 5-2 ペナルティ係数行列の作成
- 5-3 付帯条件に対する塑性化後の構成行列
- 5-4 ペナルティ係数行列の全体係数行列への組み込み
- 5-5 領域の剛性行列の作成
- 5-5 ペナルティ関数を用いた拘束条件の処理
5-1 プログラム構造
1次の変位場を有するHPMの弾性解の精度は,定ひずみ要素によるFEMの変位解と同程度の精度を有しており,弾性解析にも利用することはできる.しかし,HPMは進行型の破壊を扱う強材料非線問題に対する解析用のモデルであり,その特徴を理解するためには非線形解析法を含めて説明する必要がある.さて,本書におけるサンプル・プログラムは
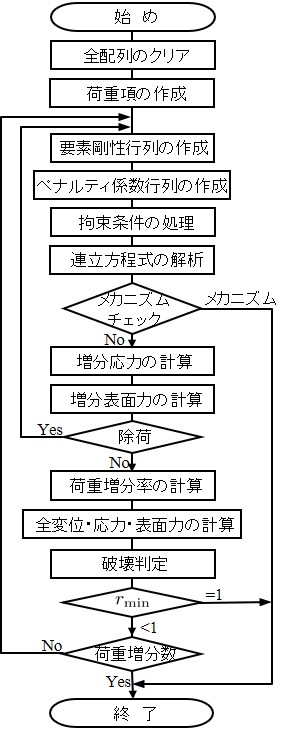
一方,材料非線形解析では各種の判定や,荷重増分に伴ういくつかの繰り返し計算が必要となる.図に示す荷重増分に関するループは本来なくてもよいもので,$r_{\rm min}$ が1になるまで繰り返し計算を行つていればよい.このようなループを設けた理由は,崩壊時近傍の荷重状態において $r_{\rm min}$ が1に収束しにくくなり,計算が暴走するのを防ぐためである.
次に,連立一次方程式を解いて変位を求めるが,この方程式は,領域内の剛性行列と付帯条件によるペナルティ係数行列から構成されている.これらの行列は,
このようにして求まった連立一次方程式を解いて得られた変位は,山田の方法による荷重増分法では仮の増分変位で,求まった値に荷重増分率がかかった値が今回の増分変位となる.これは,
構造物が崩壊機構を形成すれば,連立方程式が解けなくなり,計算を終了させることができるが,そのような状態に至らないまでも変位が急増し,その後の計算にあまり意味がないような場合には計算を強制的に終了させた方がよい.このようなメカニズム・チェックの方法には最大変位を調べる方法や,荷重変位曲線の勾配を調べる方法などがあるが,本サンプルプログラムでは前者の最大変位をチェックしている.この方法を用いる場合は $r_{\rm min}$ 倍された後の全変位で行わない方がよい.これは,仮の増分変位が大きくても荷重増分率が極端に小さいと,両者を掛け合わせた今回の増分変位が小さくなり,前回の変位に増分変位を加えた全変位が前回とあまり変わらなくなるためである.崩壊荷重時近傍ではこのような現象がたびたび生じるため,メカニズム・チェックは何らかの方法で必ず組み込んでおいた方がよいであろう.
非線形解析のもう一つの特徴として,除荷,負荷がある.この過程を設けていないと崩壊荷重や極限荷重が実際と異なって求まることがある.特にHPMではペナルティ境界辺を切断したりするため,除荷を認めておかないと,除荷が発生した場合,本来と異なった構造を解いていることになる.通常の単調載荷の場合にはあまり除荷は発生しないが,得られる解の信頼性を増すためにもこの過程は組み込んでおく必要がある.なお,本プログラムでは除荷発生後,ペナルティ関数を弾性状態に戻して再計算を行うようにしている.
最後に,荷重増分率を計算し,全変位及び全表面力・全応力を求め,それを今回の値として破壊状態を調べる.荷重増分率の累計が1になったら,全荷重が作用し終わったものとして計算を終了させる.荷重増分率が1以下ならさらに載荷を行い上記と同様な手順を繰り返す.
このような計算の流れをプログラム化したものが
本章では,このような解析の流れのうち,全体係数行列を作成し,解析して変位を求める過程を中心として説明し,その後の領域内の応力や,領域境界間の表面力の計算については次章において詳細を説明する.524 !========================================================================== 572 SUBROUTINE Analysis( Node, Element, Material, Spring, Load, Boundary, & 573 Nonlinear, Solver, File) 574 575 TYPE(typeNode), INTENT(IN) :: Node 576 TYPE(typeElement), INTENT(INOUT) :: Element 577 TYPE(typeMaterial), INTENT(IN) :: Material 578 TYPE(typeSpring), INTENT(INOUT) :: Spring 579 TYPE(typeLoad), INTENT(IN) :: Load 580 TYPE(typeBoundary), INTENT(INOUT) :: Boundary 581 TYPE(typeNonLinear),INTENT(INOUT) :: NonLinear 582 TYPE(typeBand), INTENT(INOUT) :: Solver 583 TYPE(typeFile), INTENT(IN) :: File 584 INTEGER :: iste,jramc,jramd,error 585 586 Nonlinear%rmin = 0.D0 587 CALL ClearArray(Element,Spring) 588 CALL formLoad(Node,Element,Material,Load,Boundary,Line) 589 iste = 0 590 Iteration : DO WHILE(.TRUE.) 591 iste = iste + 1 592 jramc = 0 593 jramd = 1 594 ! unloading & loading again iteration ===> 595 Unload : DO WHILE( jramd == 1) 596 Solver%stiff = 0.D0 597 Solver%load = Element%load 598 CALL formElemStiff(Node,Element,Material,Solver) 599 CALL formStiff(Node,Element,Material,Spring,Line,Solver) 600 CALL setBoundary(Node,Element,Spring,Boundary,Line,Solver) 601 CALL Solve(Solver%no,Solver%width,Solver%stiff,Solver%load,error) 602 Element%ddisp = Solver%load 603 IF(.not. MechanismCheck(Element,File,error)) RETURN 604 CALL ElementStress(Element,Material) 605 CALL SpringStress(Node,Element,Material,Spring,Line,jramc,jramd) 606 IF(jramd == 1) CYCLE Unload 607 CALL Reaction(Node,Element,Material,Load,Boundary,Line) 608 CALL incRatio(Element,Material,Spring,Nonlinear) 609 CALL totalValue(Element,Spring,Nonlinear) 610 CALL YieldCheck(Element,Material,Spring) 611 CALL Output(iste,Element,Spring,Nonlinear,File) 612 END DO Unload 613 IF(NonLinear%rmin > 0.998D0) EXIT 614 IF(iste == NonLinear%iteration) EXIT 615 END DO Iteration 616 END SUBROUTINE Analysis
5-2 ペナルティ係数行列の作成
HPMの離散化方程式には,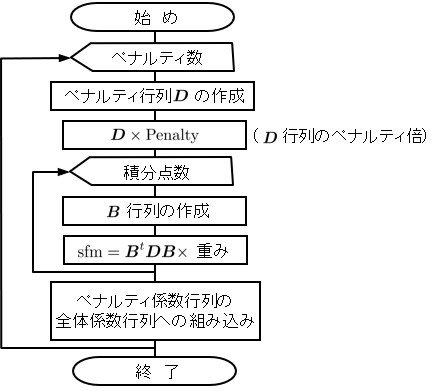
さて,数値積分に直接関係するのが818 !-------------------------------------------------------------------------- 819 SUBROUTINE formStiff( Node, Element, Material, Spring, Line, Solver) 820 821 TYPE(typeNode), INTENT(IN) :: Node 822 TYPE(typeElement), INTENT(IN) :: Element 823 TYPE(typeMaterial), INTENT(IN) :: Material 824 TYPE(typeSpring), INTENT(IN) :: Spring 825 TYPE(typeNumInteg), INTENT(IN) :: Line 826 TYPE(typeBand), INTENT(INOUT) :: Solver 827 REAL(8) :: sfm(12,12),bb(2,12),D(2,2),h,thick,wt 828 INTEGER :: is,ip,ie1,ie2,im1,im2 829 830 DO is = 1, Spring%no 831 sfm = 0.D0 832 ie1 = Spring%element(1,is) 833 ie2 = Spring%element(2,is) 834 im1 = Element%material(ie1) 835 im2 = Element%material(ie2) 836 h = Spring%hline(1,is) + Spring%hline(2,is) 837 thick = (Material%thick(im1)*Spring%hline(1,is) & 838 + Material%thick(im2)*Spring%hline(2,is))/h 839 CALL formSpring(is,Element,Material,Spring,D) 840 D = D*Spring%penalty 841 DO ip = 1, Line%no 842 CALL formB(is,ip,Node,Element,Spring,Line,bb) 843 wt = 0.5*Line%weight(ip)*Spring%length(is)/h*thick 844 sfm = sfm + MATMUL(MATMUL(TRANSPOSE(bb),D),bb)*wt 845 END DO 846 CALL Assemble(is,sfm,Spring,Solver) 847 END DO 848 END SUBROUTINE formStiff
| i | 1 | 2 | 3 |
|---|---|---|---|
| $\eta_i$ | $-\sqrt{3/5}$ | 0 | $\sqrt{3/5}$ |
| $w_i$ | $5/9$ | $8/9$ | $5/9$ |
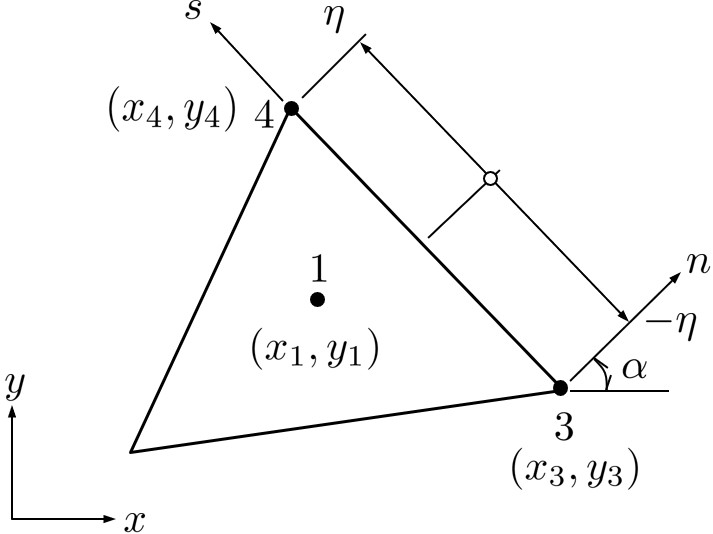
849 !-------------------------------------------------------------------------- 850 SUBROUTINE formB( is, ip, Node, Element, Spring, Line, bb ) 851 852 INTEGER, INTENT(IN) :: is 853 INTEGER, INTENT(IN) :: ip 854 TYPE(typeNode), INTENT(IN) :: Node 855 TYPE(typeElement), INTENT(IN) :: Element 856 TYPE(typeSpring), INTENT(IN) :: Spring 857 TYPE(typeNumInteg), INTENT(IN) :: Line 858 REAL(8), INTENT(OUT) :: bb(:,:) 859 860 INTEGER :: in1,in2,ie1,ie2,i 861 REAL(8) :: l(2),m(2),x35,y35,xg1,yg1,xg2,yg2,xeta1,yeta1,xeta2,yeta2 862 REAL(8) :: x5g1,x3g1,y5g1,y3g1,x5g2,x3g2,y5g2,y3g2 863 864 in1 = Spring%node(1,is) 865 in2 = Spring%node(2,is) 866 ie1 = Spring%element(1,is) 867 ie2 = Spring%element(2,is) 868 x35 = Node%coord(1,in2) - Node%coord(1,in1) 869 y35 = Node%coord(2,in2) - Node%coord(2,in1) 870 l(1) = y35/Spring%length(is) 871 l(2) = x35/Spring%length(is) 872 m(1) =-l(2) 873 m(2) = l(1) 874 xg1 = Element%center(1,ie1) 875 yg1 = Element%center(2,ie1) 876 xg2 = Element%center(1,ie2) 877 yg2 = Element%center(2,ie2) 878 x5g1 = Node%coord(1,in1) - xg1 879 x3g1 = Node%coord(1,in2) - xg1 880 y5g1 = Node%coord(2,in1) - yg1 881 y3g1 = Node%coord(2,in2) - yg1 882 x5g2 = Node%coord(1,in1) - xg2 883 x3g2 = Node%coord(1,in2) - xg2 884 y5g2 = Node%coord(2,in1) - yg2 885 y3g2 = Node%coord(2,in2) - yg2 886 xeta1 = 0.5*(x35*Line%point(ip)+x5g1+x3g1) 887 yeta1 = 0.5*(y35*Line%point(ip)+y5g1+y3g1) 888 xeta2 = 0.5*(x35*Line%point(ip)+x5g2+x3g2) 889 yeta2 = 0.5*(y35*Line%point(ip)+y5g2+y3g2) 890 DO i = 1, 2 891 bb(i, 1) = -l(i) 892 bb(i, 2) = -m(i) 893 bb(i, 3) = (l(i)*yeta1-m(i)*xeta1) 894 bb(i, 4) = -l(i)*xeta1 895 bb(i, 5) = -m(i)*yeta1 896 bb(i, 6) = -0.5*(l(i)*yeta1+m(i)*xeta1) 897 bb(i, 7) = -bb(i,1) 898 bb(i, 8) = -bb(i,2) 899 bb(i, 9) = -(l(i)*yeta2-m(i)*xeta2) 900 bb(i,10) = l(i)*xeta2 901 bb(i,11) = m(i)*yeta2 902 bb(i,12) = 0.5*(l(i)*yeta2+m(i)*xeta2) 903 END DO 904 END SUBROUTINE formB
5-3 付帯条件に対する塑性化後の構成行列
本節では,ここで,923行~926行の弾性係数とポアソン比については,垂線の高さを重みとする隣接領域の値の平均値を用いる.なお,918 h = Spring%hline(1,is) + Spring%hline(2,is) 919 ie1 = Spring%element(1,is) 920 ie2 = Spring%element(2,is) 921 im1 = Element%material(ie1) 922 im2 = Element%material(ie2) 923 E = (Material%young(im1)*Spring%hline(1,is) & 924 + Material%young(im2)*Spring%hline(2,is))/h 925 P = (Material%poisson(im1)*Spring%hline(1,is) & 926 + Material%poisson(im2)*Spring%hline(2,is))/h 927 IF(Element%type == 0) THEN 928 D(1,1) = E*(1.0-P)/(1.0+P)/(1.0-2.0*P) 929 ELSE 930 D(1,1) = E/(1.0-P**2) 931 END IF 932 D(2,2) = E/(1.0+P)
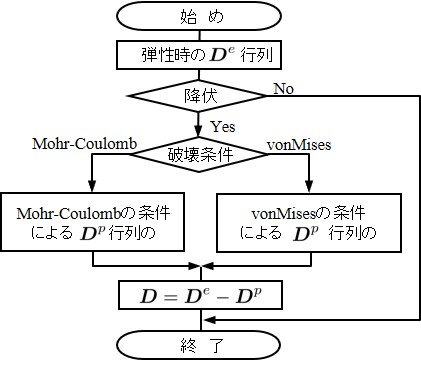
具体的なコードを
ここで,配列(Dp)は,$\boldsymbol{D}^{p}$ 行列であり,941行で $\boldsymbol{D}^{e}$ 行列から下記のごとく引いている. \[ \boldsymbol{D} = \boldsymbol{D}^{e} - \boldsymbol{D}^{p} \] したがって,配列(D)は弾性状態の $\boldsymbol{D}^{e}$ から塑性化後の構成行列に変化する.なお,本プログラムでは強度定数も935行に示すよう,隣接する2要素の垂線を重みとして平均化した値を用いている.905 !-------------------------------------------------------------------------- 906 SUBROUTINE formSpring( is, Element, Material, Spring, D ) 907 908 INTEGER, INTENT(IN) :: is 909 TYPE(typeElement), INTENT(IN) :: Element 910 TYPE(typeMaterial), INTENT(IN) :: Material 911 TYPE(typeSpring), INTENT(IN) :: Spring 912 REAL(8), INTENT(INOUT) :: D(:,:) 913 REAL(8) :: Dp(2,2),E,P,phi,h 914 INTEGER :: ie1,ie2,im1,im2 915 916 D = 0.D0 : : (弾性状態の構成行列 : プログラム5.4参照) : 933 IF(Spring%flag(is) == 1) THEN 934 IF(Element%type == 0) THEN 935 phi = (Material%phi(im1)*Spring%hline(1,is) & 936 + Material%phi(im2)*Spring%hline(2,is))/h 937 CALL MohrCoulomb(is,phi,Spring,D,Dp) 938 ELSE 939 CALL vonMises(is,Spring,D,Dp) 940 END IF 941 D = D - Dp 942 END IF 943 END SUBROUTINE formSpring
もし,本書で取り扱つているMohr-Coulombの条件やvonMisesの条件以外の破壊条件を利用したい場合はこの
次に,それぞれの破壊条件に対する $\boldsymbol{D}^{p}$ 行列の作成を
963行ではせん断に関する表面力の符号をチェックしている.これは,944 !-------------------------------------------------------------------------- 945 SUBROUTINE MohrCoulomb( is, phi, Spring, D, Dp ) 946 947 INTEGER, INTENT(IN) :: is 948 REAL(8), INTENT(IN) :: phi 949 TYPE(typeSpring), INTENT(IN) :: Spring 950 REAL(8), INTENT(IN) :: D(:,:) 951 REAL(8), INTENT(OUT) :: Dp(:,:) 952 INTEGER :: i,j 953 REAL(8) :: pt,f,D1,D2 954 REAL(8) :: PAI = 3.141592654D0 955 956 pt = DTAN(phi*PAI/180.D0) 957 D1 = D(1,1) 958 D2 = D(2,2) 959 f = 1.D0/(D2+D1*pt**2) 960 Dp(1,1) = (D1*pt)**2*f 961 Dp(2,2) = D2*D2*f 962 Dp(1,2) = D1*D2*pt*f 963 IF(Spring%stress(2,is) .LT. 0.D0) THEN 964 Dp(1,2) = -Dp(1,2) 965 END IF 966 Dp(2,1) = Dp(1,2) 967 END SUBROUTINE MohrCoulomb
968 !-------------------------------------------------------------------------- 969 SUBROUTINE vonMises( is, Spring, D, Dp ) 970 971 INTEGER, INTENT(IN) :: is 972 TYPE(typeSpring), INTENT(IN) :: Spring 973 REAL(8), INTENT(IN) :: D(:,:) 974 REAL(8), INTENT(OUT) :: Dp(:,:) 975 REAL(8) :: sig,tau,f,D1,D2 976 INTEGER :: i,j 977 978 D1 = D(1,1) 979 D2 = D(2,2) 980 sig = Spring%stress(1,is) 981 tau = Spring%Stress(2,is) 982 f = 1.D0/(D1*sig*sig/4.D0 + 4.D0*D2*tau*tau) 983 Dp(1,1) = D1*D1*sig*sig/4.D0*f 984 Dp(2,2) = 4.D0*D2*D2*tau*tau*f 985 Dp(1,2) = D1*D2*sig*tau*f 986 Dp(2,1) = Dp(1,2) 987 END SUBROUTINE vonMises
5-4 ペナルティ係数行列の全体係数行列への組み込み
本サンプル・プログラムでは全体係数行列をバンド法により解いている.メモリーを効率よく利用するためには全体係数行列を1次元配列にするとよく,このような方法はFEMにおいても頻繁に行われている.HPMの場合,ペナルティ係数行列を全体係数行列に組み込むことになるが,組み込み方法もFEMにおける節点及び要素を,それぞれ,HPMの小領域とペナルティ辺に対応させれば,組み込み方法はFEMの場合と全く同様となる.詳細については他の書物にゆずるとし,ここではどのように全体係数行列を1次元配列にセットするかについて説明する.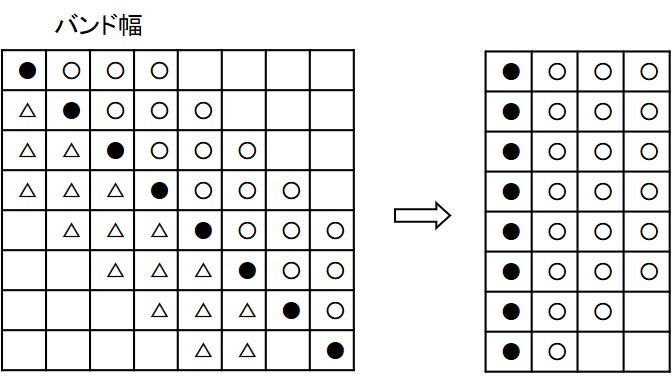
$\hspace{5em}$

以上の考えをもとにプログラム化したものが,
本サプルーチンはバンド法のための全体係数行列を作成するものであり,連立方程式の解析法を,例えばスカイライン法など他の解法に変更する場合には本サブルーチンもそれに対応するよう取り替える必要がある.988 !-------------------------------------------------------------------------- 989 SUBROUTINE Assemble( is, sfm, Spring, Solver) 990 991 INTEGER, INTENT(IN) :: is 992 REAL(8), INTENT(IN) :: sfm(:,:) 993 TYPE(typeSpring), INTENT(IN) :: Spring 994 TYPE(typeBand), INTENT(INOUT) :: Solver 995 996 INTEGER :: ie1,ie2,i,j,k,l,k1,ka,kb,la,lb 997 998 DO i = 1, 2 999 ie1 = Spring%element(i,is) 1000 DO j = i, 2 1001 ie2 = Spring%element(j,is) 1002 DO k = 1, Element%dof 1003 k1 = k 1004 IF(i /= j) THEN 1005 k1 = 1 1006 END IF 1007 DO l = k1, Element%dof 1008 ka = k + (i-1)*Element%dof 1009 kb = l + (j-1)*Element%dof 1010 la = k + (ie1-1)*Element%dof 1011 lb = l + (ie2-1)*Element%dof 1012 IF(lb .LT. la) THEN 1013 kb = k + (i-1)*Element%dof 1014 ka = l + (j-1)*Element%dof 1015 lb = k + (ie1-1)*Element%dof 1016 la = l + (ie2-1)*Element%dof 1017 END IF 1018 lb = lb + (la-1)*Solver%width - la + 1 1019 Solver%stiff(lb) = Solver%stiff(lb) + sfm(ka,kb) 1020 END DO 1021 END DO 1022 END DO 1023 END DO 1024 END SUBROUTINE Assemble
5-5 領域の剛性行列の作成
HPMでは領域内の剛性を評価することで,小領域の変形を表現している.本サンプル・プログラムでは,変位場として線形の変位場を用いているため,領域内のひずみは一定となる.これを考慮して各小領域内の剛性行列を誘導する.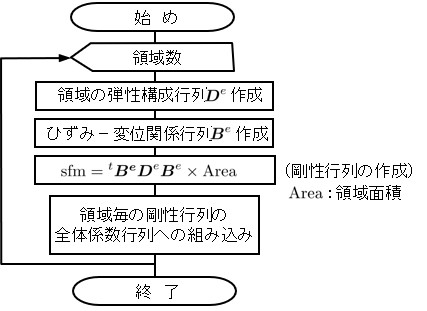
$\hspace{10em}$全体係数行列への組み込み (formElemStiff)
具体的な構成行列を作成しているプログラムを735 !-------------------------------------------------------------------------- 736 SUBROUTINE formElemStiff( Node, Element, Material, Solver) 737 738 TYPE(typeNode), INTENT(IN) :: Node 739 TYPE(typeElement), INTENT(IN) :: Element 740 TYPE(typeMaterial), INTENT(IN) :: Material 741 TYPE(typeBand), INTENT(INOUT) :: Solver 742 743 REAL(8) :: sfm(6,6),D(3,3),bb(3,6),volume 744 INTEGER :: ie,im 745 746 DO ie = 1, Element%no 747 IF(Element%node(3,ie) /= 0) THEN 748 sfm = 0.D0 749 CALL formDmatrix(ie,Element,Material,D) 750 CALL formBelem(bb) 751 im = Element%material(ie) 752 volume = Element%area(ie)*Material%thick(im) 753 sfm = sfm + MATMUL(TRANSPOSE(bb),MATMUL(D,bb))*volume 754 CALL AssembleElement(ie,sfm,Solver) 755 END IF 756 END DO 757 END SUBROUTINE formElemStiff
本サンプル・プログラムでは,領域内の応力状態として弾性のみを仮定している.もし,領域内の材料非線形を考慮するなら,降伏した要素に対し,758 !-------------------------------------------------------------------------- 759 SUBROUTINE formDmatrix( ie, Element, Material, D) 760 761 INTEGER, INTENT(IN) :: ie 762 TYPE(typeElement), INTENT(IN) :: Element 763 TYPE(typeMaterial), INTENT(IN) :: Material 764 REAL(8), INTENT(OUT) :: D(:,:) 765 766 INTEGER :: im 767 REAL(8) :: e,p,ep 768 769 D = 0.D0 770 771 im = Element%material(ie) 772 e = Material%young(im) 773 p = Material%poisson(im) 774 SELECT CASE(Element%type) 775 CASE(0) ! 平面ひずみ 776 ep = e*(1.D0-p)/(1.D0+p)/(1.D0-2.D0*p) 777 D(1,1) = ep 778 D(1,2) = ep*p/(1.D0-p) 779 D(2,1) = D(1,2) 780 D(2,2) = ep 781 D(3,3) = 0.5*ep*(1.D0-2.D0*p)/(1.D0-p) 782 CASE(1) ! 平面応力 783 ep = e/(1.D0-p*p) 784 D(1,1) = ep 785 D(1,2) = ep*p 786 D(2,1) = ep*p 787 D(2,2) = ep 788 D(3,3) = 0.5*ep*(1.D0-p) 789 END SELECT 790 END SUBROUTINE formDmatrix
また,
最後に,領域毎に作成された剛性行列の全体係数行列への組み込みついて説明する.HPMの自由度は,線形変位場を仮定した場合,剛体変位 $\boldsymbol{d}^{(e)}$ とひずみ $\boldsymbol{\varepsilon}^{(e}$の,それぞれ3自由度,計6自由度となる.領域の変形特性を表す構成行列 $\boldsymbol{D}^{e}$は,ひずみの自由度のみ関係するため,791 !-------------------------------------------------------------------------- 792 SUBROUTINE formBelem( bb ) 793 794 REAL(8), INTENT(OUT) :: bb(:,:) 795 796 bb = 0.D0 797 bb(1,4) = 1.D0 798 bb(2,5) = 1.D0 799 bb(3,6) = 1.D0 800 END SUBROUTINE formBelem
801 !-------------------------------------------------------------------------- 802 SUBROUTINE AssembleElement( ie, sfm, Solver) 803 804 INTEGER, INTENT(IN) :: ie 805 REAL(8), INTENT(IN) :: sfm(:,:) 806 TYPE(typeBand), INTENT(INOUT) :: Solver 807 INTEGER :: i,j,ia,ib,ii 808 809 DO i = 1, Element%dof 810 DO j = i, Element%dof 811 ia = i + (ie-1)*Element%dof 812 ib = j + (ie-1)*Element%dof 813 ii = ib + (ia-1)*Solver%width - ia + 1 814 Solver%stiff(ii) = Solver%stiff(ii) + sfm(i,j) 815 END DO 816 END DO 817 END SUBROUTINE AssembleElement
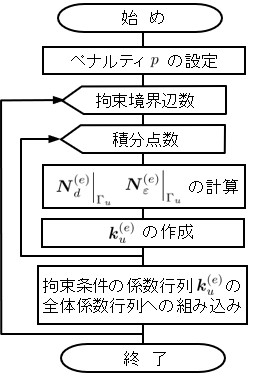
5-6 ペナルティ関数を用いた拘束条件の処理
1025 !-------------------------------------------------------------------------- 1026 SUBROUTINE setBoundary( Node, Element, Spring, Boundary, Line, Solver) 1027 1028 TYPE(typeNode), INTENT(IN) :: Node 1029 TYPE(typeElement), INTENT(IN) :: Element 1030 TYPE(typeSpring), INTENT(IN) :: Spring 1031 TYPE(typeBoundary), INTENT(IN) :: Boundary 1032 TYPE(typeNumInteg), INTENT(IN) :: Line 1033 TYPE(typeBand), INTENT(INOUT) :: Solver 1034 REAL(8) :: bsf(6,6),shape(2,6),D,t,length,wt 1035 INTEGER :: ib,e,d,n1,in2,m,p,i,j 1036 1037 D = MAXVAL( Material%young )*Spring%penalty 1038 DO ib = 1, Boundary%no 1039 bsf = 0.D0 1040 ie = Boundary%element(ib) 1041 id = Boundary%direction(ib) 1042 in1 = Boundary%node(1,ib) 1043 in2 = Boundary%node(2,ib) 1044 length = SQRT((Node%coord(1,in2)-Node%coord(1,in1))**2 & 1045 +(Node%coord(2,in2)-Node%coord(2,in1))**2) 1046 im = Element%material(ie) 1047 t = Material%thick(im) 1048 DO ip = 1, 3 1049 CALL formShape(ie,ip,in1,in2,Node,Element,Line,shape) 1050 wt = 0.5*Line%weight(ip)*length*t 1051 DO i = 1, Element%dof 1052 DO j = 1, Element%dof 1053 bsf(i,j) = bsf(i,j) + shape(id,i)*D*shape(id,j)*wt 1054 END DO 1055 END DO 1056 END DO 1057 CALL AssembleElement(ie,bsf,Solver) 1058 END DO 1059 END SUBROUTINE setBoundary
拘束する境界辺の拘束変位(強制変位)が0の場合はこの処理だけで良いが,強制変位が与えられる場合は,703 !-------------------------------------------------------------------------- 704 SUBROUTINE formShape( ie, ip, in1, in2, Node, Element, Line, shape ) 705 706 INTEGER, INTENT(IN) :: ie 707 INTEGER, INTENT(IN) :: ip 708 INTEGER, INTENT(IN) :: in1 709 INTEGER, INTENT(IN) :: in2 710 TYPE(typeNode), INTENT(IN) :: Node 711 TYPE(typeElement), INTENT(IN) :: Element 712 TYPE(typeNumInteg), INTENT(IN) :: Line 713 REAL(8), INTENT(OUT) :: shape(:,:) 714 REAL(8) :: x35,y35,x5g,y5g,x3g,y3g,xeta,yeta 715 716 shape = 0.D0 717 718 x35 = Node%coord(1,in2)-Node%coord(1,in1) 719 y35 = Node%coord(2,in2)-Node%coord(2,in1) 720 x5g = Node%coord(1,in1) - Element%center(1,ie) 721 x3g = Node%coord(1,in2) - Element%center(1,ie) 722 y5g = Node%coord(2,in1) - Element%center(2,ie) 723 y3g = Node%coord(2,in2) - Element%center(2,ie) 724 xeta = 0.5*(x35*Line%point(ip)+x5g+x3g) 725 yeta = 0.5*(y35*Line%point(ip)+y5g+y3g) 726 shape(1,1) = 1.D0 727 shape(1,3) = -yeta 728 shape(1,4) = xeta 729 shape(1,6) = 0.5*yeta 730 shape(2,2) = 1.D0 731 shape(2,3) = xeta 732 shape(2,5) = yeta 733 shape(2,6) = 0.5*xeta 734 END SUBROUTINE formShape
677 DO ib = 1, Boundary%no 678 IF(Boundary%disp(ib) /= 0.D0) THEN 679 pg = 0.D0 680 ie = Boundary%element(ib) 681 id = Boundary%direction(ib) 682 in1 = Boundary%node(1,ib) 683 in2 = Boundary%node(2,ib) 684 im = Element%material(ie) 685 t = Material%thick(im) 686 pt = Spring%penalty*MAXVAL( Material%young ) 687 length = SQRT((Node%coord(1,in2)-Node%coord(1,in1))**2 & 688 +(Node%coord(2,in2)-Node%coord(2,in1))**2) 689 DO ip = 1, 3 690 CALL formShape(ie,ip,in1,in2,Node,Element,Line,shape) 691 wt = 0.5*Line%weight(ip)*length*t 692 DO i = 1, Element%dof 693 pg(i) = pg(i) + shape(id,i)*pt*wt 694 END DO 695 END DO 696 DO i = 1, Element%dof 697 in = i + (ie-1)*Element%dof 698 Element%load(in) = Element%load(in) + pg(i)*Boundary%disp(ib) 699 END DO 700 END IF 701 END DO