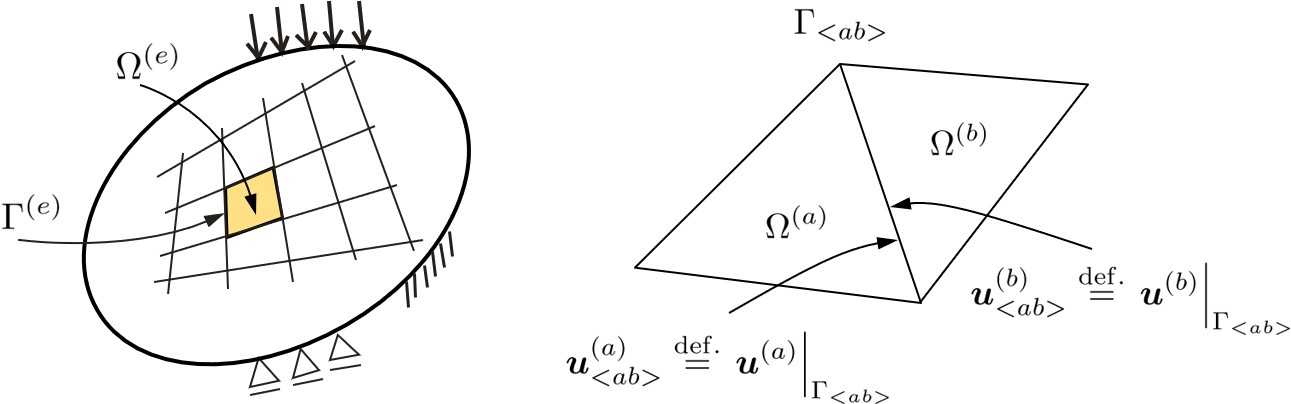いま,
図1.1に示すように,$\Omega$ を ${\rm n_{dim}}$ 次元ユークリッド空間 $\mathbb{R}^{\rm n_{\rm dim}}$ の有界領域とし,$\Gamma$ を $\Omega$ の滑らかな境界 $\Gamma := \partial \Omega$ とする.また,$\Omega$ に境界を加えてできる閉包を $\overline{\Omega} := \Omega \cup \partial \Omega $ とする.
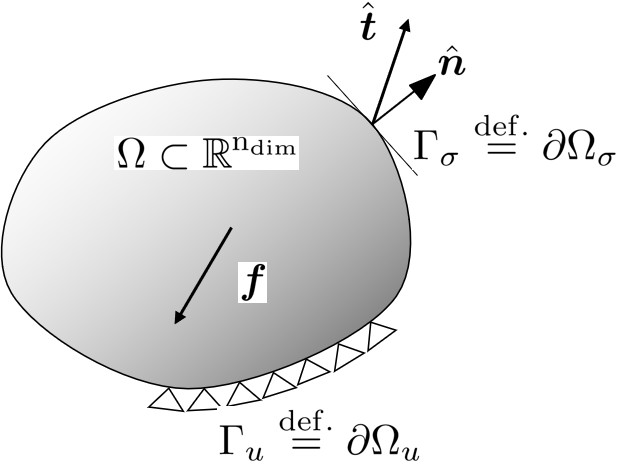
図1.1 有界領域 $\Omega$ と境界 $\Gamma$
このとき,$\Omega$ 内の弾性問題における
平衡方程式は次のように与えられる.
\[
{\rm (1.1)}
{\rm div} \boldsymbol{\sigma} + \boldsymbol{f} = 0
\quad {\rm in} \; \Omega
\]
\[
{\rm (1.2)}
\boldsymbol{\sigma} = \boldsymbol{\sigma}^t
\]
ここで,$\boldsymbol{f}:\Omega \rightarrow \mathbb{R}^{\rm n_{dim}}$ は
物体力,$\boldsymbol{\sigma}:\overline{\Omega} \rightarrow \mathbb{S}$ は
Cauchy応力である.ただし,$\mathbb{S}=\mathbb{R}^{\rm ( n_{dim}+1 ) \cdot n_{dim}/2}$ であり,${\rm n_{\rm dim}}$ 次元ユークリッド空間$\mathbb{R}^{\rm n_{\rm dim}}$ の基底ベクトルを $\boldsymbol{e}_i$ とするとき,$\boldsymbol{\sigma}=\sigma_{ij} \boldsymbol{e}_i \otimes \boldsymbol{e}_j$ である.$\boldsymbol{u}:\overline{\Omega} \rightarrow \mathbb{R}^{\rm n_{\rm dim}}$ は,$\boldsymbol{x} \in \Omega$ における
変位場で,$\boldsymbol{u} \left( \boldsymbol{x} \right)$ を簡単に$\boldsymbol{u}$とする.このとき,
微小ひずみ $\boldsymbol{\varepsilon}$ は次のように定義される.
\[
{\rm (1.3)}
\boldsymbol{\varepsilon}=\boldsymbol{\nabla}^s \boldsymbol{u}:=
\frac{1}{2}\left\{ \boldsymbol{\nabla u} + {}^t (\boldsymbol{\nabla u})\right\}
\]
ここで, $\boldsymbol{\nabla}:=\left(\partial / \partial x_i\right)\boldsymbol{e}_i$ は微分作用素であり,$\boldsymbol{\nabla}^s$ は $\boldsymbol{\nabla}$ の対称部分を表している.
一方,境界$\Gamma$ は以下の関係にある.
\[
{\rm (1.4)}
\Gamma=\Gamma_u \cup \Gamma_{\sigma}
,
\Gamma_u \cap \Gamma_{\sigma} = \emptyset
\]
ここで,$\Gamma_u:=\partial_u \Omega \subset \partial \Omega$ は変位が与えられる境界,$\Gamma_{\sigma}:=\partial_{\sigma} \Omega \subset \partial \Omega$ は表面力が与えられる境界であり,それぞれ,以下のように与えられる.
\[
{\rm (1.5)}
\left. \boldsymbol{u} \right|_{\Gamma_u} = \hat{ \boldsymbol{u} }
\;\; {\rm (given)}
\]
\[
{\rm (1.6)}
\left. \boldsymbol{\sigma} \right|_{\Gamma_{\sigma}} = \hat{ \boldsymbol{t} }
\;\; {\rm (given)}
\]
ただし,外向き法線ベクトルが $\boldsymbol{n}$ で表される物体表面の
表面力を $\boldsymbol{t}=\boldsymbol{n \sigma}$ と定義し,$\hat{\boldsymbol{n}}$を境界 $\Gamma_{\sigma}$ に対する法線ベクトルとする.ただし,上付の ^ は既知量を表している.
弾性体に対する構成方程式は,弾性テンソル$\boldsymbol{D}$を用いて次のように表される.
\[
{\rm (1.7)}
\boldsymbol{\sigma} = \boldsymbol{D : \varepsilon}
\]
いま,
式(1.7)の応力-ひずみ関係を,2次元問題に対して成分によりマトリックス表示すると次のようになる.ただし,$E$ は弾性係数,$\nu$ はポアソン比である.
(平面ひずみ)
\[
{\rm (1.8)}
\left\{
\matrix{
\sigma_x \cr
\sigma_y \cr
\tau_{xy}
}
\right\}
=
\frac{E(1-\nu)}{(1+\nu)(1-2\nu)}
\left[
\matrix{
1 & \displaystyle\frac{\nu}{1-\nu} & 0 \cr
\displaystyle\frac{\nu}{1-\nu} & 1 & 0 \cr
0 & 0 & \displaystyle \frac{1-2\nu}{2(1-\nu)}
}
\right]
\left\{
\matrix{
\varepsilon_x \cr
\varepsilon_y \cr
\gamma_{xy}
}
\right\}
\]
\[\hspace{5em}
\sigma_{z} = \frac{ \nu E}{(1+ \nu)(1-2 \nu)}
( \varepsilon_{x} + \varepsilon_{y} )
= \nu ( \sigma_x + \sigma_y)
\]
(平面応力)
\[
{\rm (1.9)}
\left\{
\matrix{
\sigma_x \cr
\sigma_y \cr
\tau_{xy}
}
\right\}
=
\frac{E}{1-\nu^2}
\left[
\begin{array}{ccc}
1 & \nu & 0 \\
\nu & 1 & 0 \\[0.5ex]
0 & 0 & \displaystyle \frac{1-\nu}{2}
\end{array}
\right]
\left\{
\matrix{
\varepsilon_x \cr
\varepsilon_y \cr
\gamma_{xy}
}
\right\}
\]
\[\hspace{5em}
\sigma_z = 0 ,
\varepsilon_z = - \frac{\nu}{1-\nu}
\left( \varepsilon_x + \varepsilon_y \right)
\]
変位 $\boldsymbol{u}$ に課せられる許容関数空間を,
\[
{\rm (1.10)}
\mathbb{U}
\stackrel{\rm def.}{=}
\left\{
\boldsymbol{u} : \Omega \rightarrow
\mathbb{R}^{\rm n_{dim}}
\left| \right.
\boldsymbol{u}|_{\Gamma_u}
=
\hat{\boldsymbol{u}}
\right\}
\]
とする.また,
仮想変位 $\delta \boldsymbol{u}$ は幾何的境界条件を満たしている.すなわち,仮想変位$\delta \boldsymbol{u}$ に課せられる許容関数空間を,
\[
{\rm (1.11)}
\mathbb{V}
\stackrel{\rm def.}{=}
\left\{
\delta \boldsymbol{u} : \Omega \rightarrow
\mathbb{R}^{\rm n_{dim}}
\left| \right.
\delta \boldsymbol{u}|_{\Gamma_u} = {\bf 0}
\right\}
\]
とする.このとき,
式(1.1)に仮想変位 $\delta \boldsymbol{u}$ を乗じて領域 $\Omega$ について積分すると,以下の関係が得られる.
\[
{\rm (1.12)}
\int_{\Omega} \delta \boldsymbol{u}
\left( {\rm div} \boldsymbol{\sigma} + \boldsymbol{f} \right) dV
= 0
\hspace{3em}
{}^{\forall}\delta \boldsymbol{u} \in \mathbb{V}
\]
式(1.12)の左辺第1項にガウスの発散定理を適用すると,変位 $\boldsymbol{u} \in \mathbb{U}$ に関する仮想仕事式が以下のように得られる.
\[
{\rm (1.13)}
\int_{\Omega}
\boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
-
\int_{\Omega} \boldsymbol{f} \! \cdot \! \delta \boldsymbol{u} dV
-
\int_{\Gamma_\sigma} \hat{\boldsymbol{t}} \! \cdot \! \delta \boldsymbol{u} \: dS
= 0
\hspace{3em}
{}^{\forall} \delta \boldsymbol{u} \in \mathbb{V}
\]
これは,$\delta \boldsymbol{u}$ を重み関数とすれば,一般的な弱形式である.このとき,$\mathbb{H}^1 \left( \Omega \right)$ をSobolev空間として,$\mathbb{U} \subset \mathbb{H}^1 \left( \Omega \right)$, $\mathbb{V} \subset \mathbb{H}^1 \left( \Omega \right)$ である.
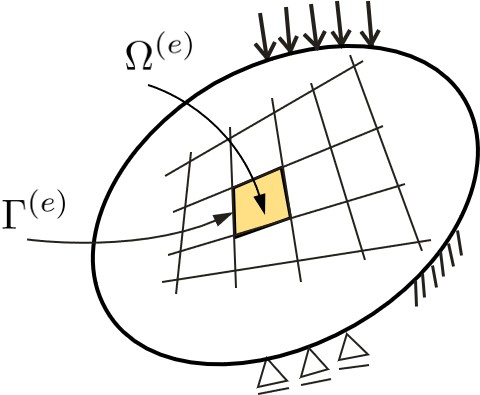
図1.2 小領域
いま,
図1.2に示すように,領域 $\Omega$ は閉境界 $\Gamma^{(e)}:=\partial \Omega^{(e)}$ で囲まれた$M$個の小領域 $\Omega^{(e)} \subset \Omega$ から構成されているものとする.すなわち,
\[
{\rm (1.14)}
\Omega = \bigcup_{e=1}^{M} \Omega^{(e)}
\hspace{2em} ただし \hspace{2em}
\Omega^{(r)} \cap \Omega^{(q)} = 0 \;\; \left( r \ne q \right)
\]
このとき,
式(1.13)の仮想仕事式は,各小領域の和として,
\[
{\rm (1.15)}
\sum_{e=1}^{M}
\left(
\int_{\Omega^{(e)}}
\boldsymbol{\sigma} \! : \!
{\rm grad}
\delta \boldsymbol{u} \: dV
-
\int_{\Omega^{(e)}} \boldsymbol{f} \! \cdot \! \delta \boldsymbol{u} dV
-
\int_{\Gamma^{(e)}}
\boldsymbol{t} \! \cdot \! \delta \boldsymbol{u} \: dS
\right)
= 0
\]
と表される.なお,$\Gamma^{(e)}$ のうち,表面力が与えられる境界が$\Gamma_{\sigma}$ となる.
図1.3に示すように,隣接する2つの小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ の共通の境界を $\Gamma_{\lt ab \gt}$ とする.
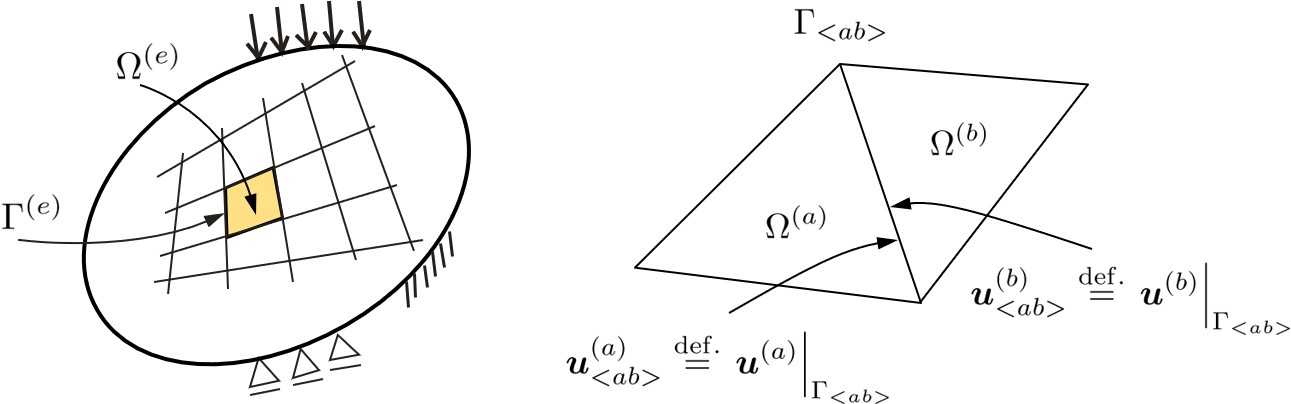
$\hspace{1em}$(a)小領域 $\Omega^{(e)}$ とその境界 $\Gamma^{(e)}$
$\hspace{3em}$(b)共通の境界 $\Gamma_{\lt ab \gt}$
$\hspace{6em}$図1.3 小領域とその共通の境界
ここで,境界 $\Gamma_{\lt ab \gt}$ は次の条件を満たしている.
\[
{\rm (1.16)}
\Gamma_{\lt ab \gt} = \Gamma^{(a)} \cap \; \Gamma^{(b)}
\]
この境界において付帯条件は,
\[
{\rm (1.17)}
\boldsymbol{u}^{(a)}_{\lt ab \gt} = \boldsymbol{u}^{(b)}_{\lt ab \gt}
\;\; {\rm on} \;\; \Gamma_{\lt ab \gt}
\]
である.ここで,$\boldsymbol{u}^{(a)}_{\lt ab \gt}$ ならびに $\boldsymbol{u}^{(b)}_{\lt ab \gt}$ は,
図1.3(b)に示すように,それぞれ,小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ における共通の境界 $\Gamma_{\lt ab \gt}$ 上の変位を表している.ハイブリッド型の仮想仕事の原理では,この付帯条件をLagrangeの未定乗数 $\boldsymbol{\lambda}$ を用いて,
\[
{\rm (1.18)}
H_{ab}
\stackrel{\rm def.}{=}
\delta \int_{\Gamma_{\lt ab \gt}} \boldsymbol{\lambda} \! \cdot \!
( \boldsymbol{u}^{(a)}_{\lt ab \gt}
- \boldsymbol{u}^{(b)}_{\lt ab \gt} )\; dS
\]
と表し,仮想仕事
式(1.15)に導入する.ただし,$\delta ( \bullet )$ は $( \bullet )$ の変分を意味している.
いま,隣接する2つの小領域境界辺の数を $N$ とすると,ハイブリッド型の仮想仕事式は次のように表すことができる.
\[
{\rm (1.19)}
\sum_{e=1}^{M}
\left(
\int_{\Omega^{(e)}} \boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
- \int_{\Omega^{(e)}} \boldsymbol{f} \! \cdot \! \delta \boldsymbol{u} dV
- \int_{\Gamma^{(e)}} \boldsymbol{t}\! \cdot \! \delta \boldsymbol{u} \: dS
\right)
\]
\[\hspace{15em}
- \sum_{s=1}^{N} \left(
\delta \int_{\Gamma_{\lt s \gt}} \boldsymbol{\lambda} \! \cdot \!
( \boldsymbol{u}^{(S_a)}_{\lt s \gt}
- \boldsymbol{u}^{(S_b)}_{\lt s \gt} )\; dS
\right)
=0
\]
ただし,領域や境界を示す上付や下付の $(e)$ や $\lt s \gt$ は省略して示している.また,左辺第3項は,便宜上,領域の和の( )内に入れておく.
なお,
式(1.19)を展開すると以下のようになる.
\[\hspace{4em}
\int_{\Omega^{(a)}} \boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
+ \cdots +
\int_{\Omega^{(b)}} \boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
\]
\[\hspace{8em}
- \int_{\Gamma_{\lt ab \gt}}
\left[
( \boldsymbol{t}^{(a)} - \boldsymbol{\lambda} ) \delta \boldsymbol{u}_{\lt ab \gt}^{(a)}
-( \boldsymbol{t}^{(b)} + \boldsymbol{\lambda} ) \delta \boldsymbol{u}_{\lt ab \gt}^{(b)}
\right.
\]
\[\hspace{16em}
+ \left. ( \boldsymbol{u}_{\lt ab \gt}^{(a)}
- \boldsymbol{u}_{\lt ab \gt}^{(b)} ) \delta \boldsymbol{\lambda} \; d S
\right]
+ \cdots = 0
\]
したがって,Lagrangeの未定乗数 $\boldsymbol{\lambda}$ は,次式のように,$\Gamma_{\lt ab \gt}$ 上の表面力を意味している.
\[
{\rm (1.20)}
\boldsymbol{\lambda} = \boldsymbol{t}^{(a)} = -\boldsymbol{t}^{(b)}
\]
ここで,$\boldsymbol{t}^{(a)}$ と $\boldsymbol{t}^{(b)}$ は,それぞれ,小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ における境界 $\Gamma_{\lt ab \gt}$ 上の表面力を表している.