９．各種剛性行列

９－１　３次元剛体要素の剛性行列

（１）３次元剛体要素の剛性行列における各成分の被積分項
\[ \begin{array}{lcl} k_{1,1} &=& l_{i}^{2}k_{i} \\ k_{1,2} &=& l_{i}m_{i}k_{i} \\ k_{1,3} &=& l_{i}n_{i}k_{i} \\ k_{1,4} &=&- l_{i}\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\}k_{i} \\ k_{1,5} &=&- l_{i}\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\}k_{i} \\ k_{1,6} &=&- l_{i}\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{1,7} &=& -k_{1,1} \\ k_{1,8} &=& -k_{1,2} \\ k_{1,9} &=& -k_{1,3} \\ k_{1,10} &=& l_{i}\{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{1,11} &=& l_{i}\{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{1,12} &=& l_{i}\{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{2,2} &=& m_{i}^{2}k_{i} \\ k_{2,3} &=& m_{i}n_{i}k_{i} \\ k_{2,4} &=&- m_{i}\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\}k_{i} \\ k_{2,5} &=&- m_{i}\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\}k_{i} \\ k_{2,6} &=&- m_{i}\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{2,7} &=& -k_{1,2} \\ k_{2,8} &=& -k_{2,2} \\ k_{2,9} &=& -k_{2,3} \\ k_{2,10} &=& m_{i}\{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{2,11} &=& m_{i}\{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{2,12} &=& m_{i}\{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{3,3} &=& n_{i}^{2}k_{i} \\ k_{3,4} &=&- n_{i}\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\}k_{i} \\ k_{3,5} &=&- n_{i}\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\}k_{i} \\ k_{3,6} &=&- n_{i}\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{3,7} &=& -k_{1,3} \\ k_{3,8} &=& -k_{2,3} \\ k_{3,9} &=& -k_{3,3} \\ k_{3,10} &=& n_{i}\{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{3,11} &=& n_{i}\{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{3,12} &=& n_{i}\{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{4,4} &=& \{m_{i}(z-z_{1})-n_{i}(y-y_{1})\}^{2}k_{i} \\ k_{4,5} &=& \{m_{i}(z-z_{1})-n_{i}(y-y_{1})\} \{n_{i}(x-x_{1})-l_{i}(z-z_{1})\}k_{i} \\ k_{4,6} &=& \{m_{i}(z-z_{1})-n_{i}(y-y_{1})\} \{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{4,7} &=& -k_{1,4} \\ k_{4,8} &=& -k_{2,4} \\ k_{4,9} &=& -k_{3,4} \\ k_{4,10} &=& -\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\} \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{4,11} &=& -\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\} \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{4,12} &=& -\{m_{i}(z-z_{1})-n_{i}(y-y_{1})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{5,5} &=& \{n_{i}(x-x_{1})-l_{i}(z-z_{1})\}^{2}k_{i} \\ k_{5,6} &=& \{n_{i}(x-x_{1})-l_{i}(z-z_{1})\} \{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{5,7} &=& -k_{1,5} \\ k_{5,8} &=& -k_{2,5} \\ k_{5,9} &=& -k_{3,5} \\ k_{5,10} &=& -\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\} \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{5,11} &=& -\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\} \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{5,12} &=& -\{n_{i}(x-x_{1})-l_{i}(z-z_{1})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{6,6} &=& \{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}^{2}k_{i} \\ k_{6,7} &=& -k_{1,6} \\ k_{6,8} &=& -k_{2,6} \\ k_{6,9} &=& -k_{3,6} \\ k_{6,10} &=& -\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\} \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}k_{i} \\ k_{6,11} &=& -\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\} \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{6,12} &=& -\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{7,7} &=& k_{1,1} \\ k_{7,8} &=& k_{1,2} \\ k_{7,9} &=& k_{1,3} \\ k_{7,10} &=& -k_{1,10} \\ k_{7,11} &=& -k_{1,11} \\ k_{7,12} &=& -k_{1,12} \\ \\ k_{8,8} &=& k_{2,2} \\ k_{8,9} &=& k_{2,3} \\ k_{8,10} &=& -k_{2,10} \\ k_{8,11} &=& -k_{2,11} \\ k_{8,12} &=& -k_{2,12} \\ \\ k_{9,9} &=& k_{3,3} \\ k_{9,10} &=& -k_{3,10} \\ k_{9,11} &=& -k_{3,11} \\ k_{9,12} &=& -k_{3,12} \\ \\ k_{10,10} &=& \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\}^{2}k_{i} \\ k_{10,11} &=& \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\} \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}k_{i} \\ k_{10,12} &=& \{m_{i}(z-z_{2})-n_{i}(y-y_{2})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{11,11} &=& \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\}^{2}k_{i} \\ k_{11,12} &=& \{n_{i}(x-x_{2})-l_{i}(z-z_{2})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \\ \\ k_{12,12} &=& \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}^{2}k_{i} \end{array} \]
ここで、記号については 1.2節で使用したものと同一で、添字については以下のように考えるものとする。
\[{\rm (9.1)}   k_1 = k_{s \overline{x}} \;,\;\; k_2 = k_{s \overline{y}} \;,\;\; k_3 = k_{n} \]
また、同一添字が繰り返して現れる場合、以下の示すような省略を行っている。
\[{\rm (9.2)}   l_i m_i k_i = \sum_{i=1}^{3} l_i m_i k_i = l_1 m_1 k_1 + l_2 m_2 k_2 + l_3 m_3 k_3 \]
（２）３次元剛体要素の剛性行列
下に示す剛性行列は積分実行後のもので、接触面を三角形としている。
\[ \begin{array}{lcl} K_{1,1} &=& l_{i}^{2}k_{i} \\ K_{1,2} &=& l_{i}m_{i}k_{i} \\ K_{1,3} &=& l_{i}n_{i}k_{i} \\ K_{1,4} &=&- l_{i}\Delta_{21_{i}}k_{i} \\ K_{1,5} &=&- l_{i}\Delta_{31_{i}}k_{i} \\ K_{1,6} &=&- l_{i}\Delta_{11_{i}}k_{i} \\ K_{1,7} &=& -K_{1,1} \\ K_{1,8} &=& -K_{1,2} \\ K_{1,9} &=& -K_{1,3} \\ K_{1,10} &=& l_{i}\Delta_{22_{i}}k_{i} \\ K_{1,11} &=& l_{i}\Delta_{32_{i}}k_{i} \\ K_{1,12} &=& l_{i}\Delta_{12_{i}}k_{i} \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{2,2} &=& m_{i}^{2}k_{i} \\ K_{2,3} &=& m_{i}n_{i}k_{i} \\ K_{2,4} &=&- m_{i}\Delta_{21_{i}}k_{i} \\ K_{2,5} &=&- m_{i}\Delta_{31_{i}}k_{i} \\ K_{2,6} &=&- m_{i}\Delta_{11_{i}}k_{i} \\ K_{2,7} &=& -K_{1,2} \\ K_{2,8} &=& -K_{2,2} \\ K_{2,9} &=& -K_{2,3} \\ K_{2,10} &=& m_{i}\Delta_{22_{i}}k_{i} \\ K_{2,11} &=& m_{i}\Delta_{32_{i}}k_{i} \\ K_{2,12} &=& m_{i}\Delta_{12_{i}}k_{i} \\ & & \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{3,3} &=& n_{i}^{2}k_{i} \\ K_{3,4} &=&- n_{i}\Delta_{21_{i}}k_{i} \\ K_{3,5} &=&- n_{i}\Delta_{31_{i}}k_{i} \\ K_{3,6} &=&- n_{i}\Delta_{11_{i}}k_{i} \\ K_{3,7} &=& -K_{1,3} \\ K_{3,8} &=& -K_{2,3} \\ K_{3,9} &=& -K_{3,3} \\ K_{3,10} &=& n_{i}\Delta_{22_{i}}k_{i} \\ K_{3,11} &=& n_{i}\Delta_{32_{i}}k_{i} \\ K_{3,12} &=& n_{i}\Delta_{12_{i}}k_{i} \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} K_{4,4} &=& \Delta_{21_{i}}^{2}k_{i} + a_{22_{ii}}k_{i} \\ K_{4,5} &=& \Delta_{21_{i}}\Delta_{31_{i}}k_{i} + a_{23_{ii}}k_{i} \\ K_{4,6} &=& \Delta_{21_{i}}\Delta_{11_{i}}k_{i} + a_{12_{ii}}k_{i} \\ K_{4,7} &=& -K_{1,4} \\ K_{4,8} &=& -K_{2,4} \\ K_{4,9} &=& -K_{3,4} \\ K_{4,10} &=&- \Delta_{21_{i}}\Delta_{22_{i}}k_{i} - a_{22_{ii}}k_{i} \\ K_{4,11} &=&- \Delta_{21_{i}}\Delta_{32_{i}}k_{i} - a_{23_{ii}}k_{i} \\ K_{4,12} &=&- \Delta_{21_{i}}\Delta_{12_{i}}k_{i} - a_{12_{ii}}k_{i} \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{5,5} &=& \Delta_{31_{i}}^{2}k_{i} + a_{33_{ii}}k_{i} \\ K_{5,6} &=& \Delta_{31_{i}}\Delta_{11_{i}}k_{i} + a_{13_{ii}}k_{i} \\ K_{5,7} &=& -K_{1,5} \\ K_{5,8} &=& -K_{2,5} \\ K_{5,9} &=& -K_{3,5} \\ K_{5,10} &=&- \Delta_{31_{i}}\Delta_{22_{i}}k_{i} - a_{23_{ii}}k_{i} \\ K_{5,11} &=&- \Delta_{31_{i}}\Delta_{32_{i}}k_{i} - a_{33_{ii}}k_{i} \\ K_{5,12} &=&- \Delta_{31_{i}}\Delta_{12_{i}}k_{i} - a_{13_{ii}}k_{i} \\ & & \end{array} \] \[ \begin{array}{lcl} K_{6,6} &=& \Delta_{11_{i}}^{2}k_{i} + a_{11_{ii}}k_{i} \\ K_{6,7} &=& -K_{1,6} \\ K_{6,8} &=& -K_{2,6} \\ K_{6,9} &=& -K_{3,6} \\ K_{6,10} &=&- \Delta_{11_{i}}\Delta_{22_{i}}k_{i} - a_{12_{ii}}k_{i} \\ K_{6,11} &=&- \Delta_{11_{i}}\Delta_{32_{i}}k_{i} - a_{13_{ii}}k_{i} \\ K_{6,12} &=&- \Delta_{11_{i}}\Delta_{12_{i}}k_{i} - a_{11_{ii}}k_{i} \end{array} \;\;\;\;\;\;\; \begin{array}{lcrl} K_{7,7} &=& \!\!&\!\!K_{1,1} \\ K_{7,8} &=& \!\!&\!\!K_{1,2} \\ K_{7,9} &=& \!\!&\!\!K_{1,3} \\ K_{7,10} &=& -\!\!&\!\!K_{1,10} \\ K_{7,11} &=& -\!\!&\!\!K_{1,11} \\ K_{7,12} &=& -\!\!&\!\!K_{1,12} \\ & & & \end{array} \;\;\;\;\;\;\; \begin{array}{lcrl} K_{8,8} &=& \!\!&\!\!K_{2,2} \\ K_{8,9} &=& \!\!&\!\!K_{2,3} \\ K_{8,10} &=& -\!\!&\!\!K_{2,10} \\ K_{8,11} &=& -\!\!&\!\!K_{2,11} \\ K_{8,12} &=& -\!\!&\!\!K_{2,12} \\ & & & \\ & & & \end{array} \] \[ \begin{array}{lcrl} K_{9,9} &=& \!\!&\!\!K_{3,3} \\ K_{9,10} &=& -\!\!&\!\!K_{3,10} \\ K_{9,11} &=& -\!\!&\!\!K_{3,11} \\ K_{9,12} &=& -\!\!&\!\!K_{3,12} \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{10,10} &=& \Delta_{22_{i}}^{2}k_{i} + a_{22_{ii}}k_{i} \\ K_{10,11} &=& \Delta_{22_{i}}\Delta_{32_{i}}k_{i} + a_{23_{ii}}k_{i} \\ K_{10,12} &=& \Delta_{22_{i}}\Delta_{12_{i}}k_{i} + a_{12_{ii}}k_{i} \\ & & \end{array} \] \[ \begin{array}{lcl} K_{11,11} &=& \Delta_{32_{i}}^{2}k_{i} + a_{33_{ii}}k_{i} \\ K_{11,12} &=& \Delta_{32_{i}}\Delta_{12_{i}}k_{i} + a_{31_{ii}}k_{i} \\ \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{12,12} &=& \Delta_{12_{i}}^{2}k_{i} + a_{11_{ii}}k_{i} \\ & & \end{array} \] \[ \left( \times A \right) \]
この剛性行列に現れる、係数 $\Delta_{ijk}$、$a_{ijkl}$ は以下の通りである。
\[ \begin{array}{lll} 3\Delta_{11_{i}} &=& l_{i}(y_{31}+y_{41}+y_{51}) - m_{i}(x_{31}+x_{41}+x_{51}) \\ 3\Delta_{21_{i}} &=& m_{i}(z_{31}+z_{41}+z_{51}) - n_{i}(y_{31}+y_{41}+y_{51}) \\ 3\Delta_{31_{i}} &=& n_{i}(x_{31}+x_{41}+x_{51}) - l_{i}(z_{31}+z_{41}+z_{51}) \\ 3\Delta_{12_{i}} &=& l_{i}(y_{32}+y_{42}+y_{52}) - m_{i}(x_{32}+x_{42}+x_{52}) \\ 3\Delta_{22_{i}} &=& m_{i}(z_{32}+z_{42}+z_{52}) - n_{i}(y_{32}+y_{42}+y_{52}) \\ 3\Delta_{32_{i}} &=& n_{i}(x_{32}+x_{42}+x_{52}) - l_{i}(z_{32}+z_{42}+z_{52}) \end{array} \] \[\hspace{2em} ( x_{ij} = x_{i} - x_{j} \;, \;\;\; y_{ij} = y_{i} - y_{j} \;, \;\;\; z_{ij} = z_{i} - z_{j} ) \] \[ a_{ijkl} = \frac{1}{36} ( \beta_{ik1}\beta_{jl1} + \beta_{ik2}\beta_{jl2} + \beta_{ik3}\beta_{jl3} ) \] \[\hspace{2em} \begin{array}{lcl} \beta_{1_{i}1} &=& -l_{i}y_{43} + m_{i}x_{43} \\ \beta_{2_{i}1} &=& -m_{i}z_{43} + n_{i}y_{43} \\ \beta_{3_{i}1} &=& -n_{i}x_{43} + l_{i}z_{43} \end{array} \;\;\;\;\; \begin{array}{lcl} \beta_{1_{i}2} &=& l_{i}y_{45} - m_{i}x_{45} \\ \beta_{2_{i}2} &=& m_{i}z_{45} - n_{i}y_{45} \\ \beta_{3_{i}2} &=& n_{i}x_{45} - l_{i}z_{45} \end{array} \;\;\;\;\; \begin{array}{lcl} \beta_{1_{i}3} &=& l_{i}y_{53} - m_{i}x_{53} \\ \beta_{2_{i}3} &=& m_{i}z_{53} - n_{i}y_{53} \\ \beta_{3_{i}3} &=& n_{i}x_{53} - l_{i}z_{53} \end{array} \]
各記号については式(9.1)と同一な関係を用いている。また、添字については、式(9.2)と同様、以下のような省略を行っている。
\[{\rm (9.3)}   \left\{ \begin{array}{l} \Delta_{22_{i}}\Delta_{32_{i}}k_{i} = \displaystyle \sum_{1=1}^{3} \Delta_{22_{i}}\Delta_{32_{i}}k_{i} = \Delta_{221}\Delta_{321}k_{1} + \Delta_{222}\Delta_{322}k_{2} + \Delta_{223}\Delta_{323}k_{3} \\ a_{23_{ii}}k_{i} = \displaystyle \sum_{i=1}^{3} a_{23_{ii}}k_{i} = a_{2311}k_{1}+a_{2322}k_{2}+a_{2333}k_{3} \end{array} \right. \]
（３）塑性化後の剛性行列
性化後ばね行列が
\[{\rm (9.4)}   [k_{ij}] = \left[ \begin{array}{ccc} k_{11} & k_{12} & k_{13} \\ k_{21} & k_{22} & k_{23} \\ k_{31} & k_{32} & k_{33} \end{array} \right] \;\;\;\; ( k_{12} = k_{21} \;, \;\; k_{13} = k_{31} \;, \;\; k_{23} = k_{32} ) \]
となった場合の剛性行列を以下に示す。
\[ \begin{array}{lcl} {K}_{1,1} &=& l_{i}l_{j}k_{ij} \\ {K}_{1,2} &=& l_{i}m_{j}k_{ij} \\ {K}_{1,3} &=& l_{i}n_{j}k_{ij} \\ {K}_{1,4} &=& -l_{i}\Delta_{21_{j}}k_{ij} \\ {K}_{1,5} &=& -l_{i}\Delta_{31_{j}}k_{ij} \\ {K}_{1,6} &=& -l_{i}\Delta_{11_{j}}k_{ij} \\ {K}_{1,7} &=& -{K}_{1,1} \\ {K}_{1,8} &=& -{K}_{1,2} \\ {K}_{1,9} &=& -{K}_{1,3} \\ {K}_{1,10} &=& l_{i}\Delta_{22_{j}}k_{ij} \\ {K}_{1,11} &=& l_{i}\Delta_{32_{j}}k_{ij} \\ {K}_{1,12} &=& l_{i}\Delta_{12_{j}}k_{ij} \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} {K}_{2,2} &=& m_{i}m_{j}k_{ij} \\ {K}_{2,3} &=& m_{i}n_{j}k_{ij} \\ {K}_{2,4} &=& -m_{i}\Delta_{21_{j}}k_{ij} \\ {K}_{2,5} &=& -m_{i}\Delta_{31_{j}}k_{ij} \\ {K}_{2,6} &=& -m_{i}\Delta_{11_{j}}k_{ij} \\ {K}_{2,7} &=& -{K}_{1,2} \\ {K}_{2,8} &=& -{K}_{2,2} \\ {K}_{2,9} &=& -{K}_{2,3} \\ {K}_{2,10} &=& m_{i}\Delta_{22_{j}}k_{ij} \\ {K}_{2,11} &=& m_{i}\Delta_{32_{j}}k_{ij} \\ {K}_{2,12} &=& m_{i}\Delta_{12_{j}}k_{ij} \\ & & \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} {K}_{3,3} &=& n_{i}n_{j}k_{ij} \\ {K}_{3,4} &=& -n_{i}\Delta_{21_{j}}k_{ij} \\ {K}_{3,5} &=& -n_{i}\Delta_{31_{j}}k_{ij} \\ {K}_{3,6} &=& -n_{i}\Delta_{11_{j}}k_{ij} \\ {K}_{3,7} &=& -{K}_{1,3} \\ {K}_{3,8} &=& -{K}_{2,3} \\ {K}_{3,9} &=& -{K}_{3,3} \\ {K}_{3,10} &=& n_{i}\Delta_{22_{j}}k_{ij} \\ {K}_{3,11} &=& n_{i}\Delta_{32_{j}}k_{ij} \\ {K}_{3,12} &=& n_{i}\Delta_{12_{j}}k_{ij} \\ & & \\ & & \end{array} \] \[ \begin{array}{lll} {K}_{4,4} &=& \Delta_{21_{i}}\Delta_{21_{j}}k_{ij} + a_{22_{ij}}k_{ij} \\ {K}_{4,5} &=& \Delta_{21_{i}}\Delta_{31_{j}}k_{ij} + a_{23_{ij}}k_{ij} \\ {K}_{4,6} &=& \Delta_{21_{i}}\Delta_{11_{j}}k_{ij} + a_{21_{ij}}k_{ij} \\ {K}_{4,7} &=&-{K}_{1,4} \\ {K}_{4,8} &=&-{K}_{2,4} \\ {K}_{4,9} &=&-{K}_{3,4} \\ {K}_{4,10} &=&-\Delta_{21_{i}}\Delta_{22_{j}}k_{ij} - a_{22_{ij}}k_{ij} \\ {K}_{4,11} &=&-\Delta_{21_{i}}\Delta_{32_{j}}k_{ij} - a_{23_{ij}}k_{ij} \\ {K}_{4,12} &=&-\Delta_{21_{i}}\Delta_{12_{j}}k_{ij} - a_{21_{ij}}k_{ij} \end{array} \;\;\;\;\;\;\; \begin{array}{lll} {K}_{5,5} &=& \Delta_{31_{i}}\Delta_{31_{j}}k_{ij} + a_{33_{ij}}k_{ij} \\ {K}_{5,6} &=& \Delta_{31_{i}}\Delta_{11_{j}}k_{ij} + a_{31_{ij}}k_{ij} \\ {K}_{5,7} &=&-{K}_{1,5} \\ {K}_{5,8} &=&-{K}_{2,5} \\ {K}_{5,9} &=&-{K}_{3,5} \\ {K}_{5,10} &=&-\Delta_{31_{i}}\Delta_{22_{j}}k_{ij} - a_{32_{ij}}k_{ij} \\ {K}_{5,11} &=&-\Delta_{31_{i}}\Delta_{32_{j}}k_{ij} - a_{33_{ij}}k_{ij} \\ {K}_{5,12} &=&-\Delta_{31_{i}}\Delta_{12_{j}}k_{ij} - a_{31_{ij}}k_{ij} \\ \\ \end{array} \] \[ \begin{array}{lll} {K}_{6,6} &=& \Delta_{11_{i}}\Delta_{11_{j}}k_{ij} + a_{11_{ij}}k_{ij} \\ {K}_{6,7} &=&-{K}_{1,6} \\ {K}_{6,8} &=&-{K}_{2,6} \\ {K}_{6,9} &=&-{K}_{3,6} \\ {K}_{6,10} &=&-\Delta_{11_{i}}\Delta_{22_{j}}k_{ij} - a_{12_{ij}}k_{ij} \\ {K}_{6,11} &=&-\Delta_{11_{i}}\Delta_{32_{j}}k_{ij} - a_{13_{ij}}k_{ij} \\ {K}_{6,12} &=&-\Delta_{11_{i}}\Delta_{12_{j}}k_{ij} - a_{11_{ij}}k_{ij} \\ \end{array} \;\;\;\;\;\;\; \begin{array}{lcrl} {K}_{7,7} &=& \!\!&\!\!{K}_{1,1} \\ {K}_{7,8} &=& \!\!&\!\!{K}_{1,2} \\ {K}_{7,9} &=& \!\!&\!\!{K}_{1,3} \\ {K}_{7,10} &=& -\!\!&\!\!{K}_{1,10} \\ {K}_{7,11} &=& -\!\!&\!\!{K}_{1,11} \\ {K}_{7,12} &=& -\!\!&\!\!{K}_{1,12} \\ & & & \end{array} \;\;\;\;\;\;\; \begin{array}{lcrl} {K}_{8,8} &=& \!\!&\!\!{K}_{2,2} \\ {K}_{8,9} &=& \!\!&\!\!{K}_{2,3} \\ {K}_{8,10} &=& -\!\!&\!\!{K}_{2,10} \\ {K}_{8,11} &=& -\!\!&\!\!{K}_{2,11} \\ {K}_{8,12} &=& -\!\!&\!\!{K}_{2,12} \\ & & & \\ & & & \end{array} \] \[ \begin{array}{lcrl} {K}_{9,9} &=& \!\!&\!\!{K}_{3,3} \\ {K}_{9,10} &=& -\!\!&\!\!{K}_{3,10} \\ {K}_{9,11} &=& -\!\!&\!\!{K}_{3,11} \\ {K}_{9,12} &=& -\!\!&\!\!{K}_{3,12} \end{array} \;\;\;\;\;\;\; \begin{array}{lll} {K}_{10,10} &=& \Delta_{22_{i}}\Delta_{22_{i}}k_{ij} + a_{22_{ij}}k_{ij} \\ {K}_{10,11} &=& \Delta_{22_{i}}\Delta_{32_{j}}k_{ij} + a_{23_{ij}}k_{ij} \\ {K}_{10,12} &=& \Delta_{22_{i}}\Delta_{12_{j}}k_{ij} + a_{21_{ij}}k_{ij} \\ & & \end{array} \] \[ \begin{array}{lll} {K}_{11,11} &=& \Delta_{32_{i}}\Delta_{32_{j}}k_{ij} + a_{33_{ij}}k_{ij} \\ {K}_{11,12} &=& \Delta_{32_{i}}\Delta_{12_{j}}k_{ij} + a_{31_{ij}}k_{ij} \end{array} \;\;\;\;\;\;\; \begin{array}{lll} {K}_{12,12} &=& \Delta_{12_{i}}\Delta_{12_{j}}k_{ij} + a_{11_{ij}}k_{ij} \\ & & \end{array} \] \[ \left( \times A \right) \]
記号および添字の関係は、これまでと同一であり、添字については以下のような省略を行っている。
\[{\rm (9.5)}   l_{i}m_{j}k_{ij} = \displaystyle \sum_{i=1}^{3} \sum_{j=1}^{3} l_{i}m_{j}k_{ij} \]

９－２　面内変形平面要素の剛性行列

（１）面内変形平面要素の剛性行列における各成分の被積分項
 表現を簡潔にするためには、面内変形平面要素に限定した記号の再定義を行うと都合がよい。そこで、図9.1に示すように要素重心の剛体変位ならびに外力の記号を以下のように読み変える。
 
$\hspace{0em}$図9.1　面内変形平面要素の自由度，荷重
\[\hspace{2em} u \rightarrow u \;, \;\;\;\; v \rightarrow v \;, \;\;\;\; \chi \rightarrow \theta \;, \;\;\;\;\; X \rightarrow X \;, \;\;\;\; Y \rightarrow Y \;, \;\;\;\; N \rightarrow M \]
このように定義すると式(1.20)に示した自由度、ならびに外力項は以下のように書き換えられる。
\[\hspace{2em} \boldsymbol{u} = (u_{1} \;, \;\; v_{1} \;, \;\; \theta_{1} \;, \;\; u_{2} \;, \;\; v_{2} \;, \;\; \theta_{2} ) \;, \;\;\;\;\; \boldsymbol{F} = (X_{1} \;, \;\; Y_{1} \;, \;\; M_{1} \;, \;\; X_{2} \;, \;\; Y_{2} \;, \;\; M_{2} ) \]
また、9.1節で示した３次元の一般的な式において、方向余弦とばね定数の添字を以下に示すよう読み変える。
\[\hspace{2em} l_{3} \rightarrow l_{2} \;, \;\;\;\; m_{3} \rightarrow m_{2} \;, \;\;\;\; k_{3} \rightarrow k_{2} \]
この結果、それぞれの方向余弦、ならびに、ばね定数は以下のようになる。
\[\hspace{2em} l_{1} = \frac{x_{43}}{L} \;, \;\;\;\; m_{1} = \frac{y_{43}}{L} \;, \;\;\;\; l_{2} = \frac{y_{43}}{L} \;, \;\;\;\; m_{2} = -\frac{x_{43}}{L} \] \[\hspace{2em} k_{1} = k_{s \overline{x}} \;, \;\;\;\; k_{2} = k_{n} \]
上の前提のもと、３次元の剛性行列における各成分の被積分項を面内変形平面要素用に変形すると以下の式が得られる。
\[ \begin{array}{lcl} k_{1,1} &=& l_{i}^{2}k_{i} \\ k_{1,2} &=& l_{i}m_{i}k_{i} \\ k_{1,3} &=&- l_{i}\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{1,4} &=& -k_{1,1} \\ k_{1,5} &=& -k_{1,2} \\ k_{1,6} &=& l_{i}\{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \end{array} \] \[ \begin{array}{lcl} k_{2,2} &=& m_{i}^{2}k_{i} \\ k_{2,3} &=&- m_{i}\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}k_{i} \\ k_{2,4} &=& -k_{1,2} \\ k_{2,5} &=& -k_{2,2} \\ k_{2,6} &=& m_{i}\{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \end{array} \] \[ \begin{array}{lcl} k_{3,3} &=& \{l_{i}(y-y_{1})-m_{i}(x-x_{1})\}^{2}k_{i} \\ k_{3,4} &=& -k_{1,3} \\ k_{3,5} &=& -k_{2,3} \\ k_{3,6} &=& -\{l_{i}(y-y_{1})-m_{i}(x-x_{1})\} \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}k_{i} \end{array} \] \[ \begin{array}{lcrl} k_{4,4} &=& \!\!&\!\!k_{1,1} \\ k_{4,5} &=& \!\!&\!\!k_{1,2} \\ k_{4,6} &=& -\!\!&\!\!k_{1,6} \end{array} \;\;\;\;\; \begin{array}{lcrl} k_{5,5} &=& \!\!&\!\!k_{2,2} \\ k_{5,6} &=& -\!\!&\!\!k_{2,6} \\ & & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{6,6} &=& \{l_{i}(y-y_{2})-m_{i}(x-x_{2})\}^{2}k_{i} \\ & & \\ & & \end{array} \]
ここで、同一添字が繰り返して現れる場合、9.1節と同様、以下の示すような省略を行っている。
\[{\rm (9.6)}   l_{i}m_{i}k_{i} = \displaystyle \sum_{i=1}^{2} l_{i}m_{i}k_{i} = l_{1}m_{1}k_{1} + l_{2}m_{2}k_{2} \]
（２）面内変形平面要素の剛性行列
 9.2(1)節に示した被積分項を接触面が長方形として積分を実行した後の面内変形平面要素の剛性行列を以下に示す。
\[ \begin{array}{lll} \begin{array}{lcl} K_{1,1} &=& l_{i}^{2}k_{i} \\ K_{1,2} &=& l_{i}m_{i}k_{i} \\ K_{1,3} &=&- l_{i}\Delta_{1_{i}}k_{i} \\ K_{1,4} &=& -K_{1,1} \\ K_{1,5} &=& -K_{1,2} \\ K_{1,6} &=& l_{i}\Delta_{2_{i}}k_{i} \end{array} \;\;\;\;\; &\begin{array}{lcl} K_{2,2} &=& m_{i}^{2}k_{i} \\ K_{2,3} &=&- m_{i}\Delta_{1_{i}}k_{i} \\ K_{2,4} &=& -K_{1,2} \\ K_{2,5} &=& -K_{2,2} \\ K_{2,6} &=& m_{i}\Delta_{2_{i}}k_{i} \\ & & \end{array} \;\;\;\;\; &\begin{array}{lcl} K_{3,3} &=& \Delta_{1_{i}}^{2}k_{i} + a_{ii}k_{i} \\ K_{3,4} &=& -K_{1,3} \\ K_{3,5} &=& -K_{2,3} \\ K_{3,6} &=&- \Delta_{1_{i}}\Delta_{2_{i}}k_{i} - a_{ii}k_{i} \\ & & \\ & & \end{array} \\ \\ \begin{array}{lcrl} K_{4,4} &=& \!\!&\!\!K_{1,1} \\ K_{4,5} &=& \!\!&\!\!K_{1,2} \\ K_{4,6} &=& -\!\!&\!\!K_{1,6} \\ \end{array} \;\;\;\;\; &\begin{array}{lcrl} K_{5,5} &=& \!\!&\!\!K_{2,2} \\ K_{5,6} &=& -\!\!&\!\!K_{2,6} \\ & & & \end{array} \;\;\;\;\; &\begin{array}{lcl} K_{6,6} &=& \Delta_{2_{i}}^{2}k_{i} + a_{ii}k_{i} \\ & & \\ & & \end{array} \end{array} \] \[ ( \times L ) \]
各記号については式(9.5)と同一な関係を用いている。また、添字については、式(9.5)と同様、以下のような省略を行っている。
\[{\rm (9.7)}   \left\{ \begin{array}{l} \Delta_{1_{i}}\Delta_{2_{i}}k_{i} = \displaystyle \sum_{1=1}^{2} \Delta_{1_{i}}\Delta_{2_{i}}k_{i} = \Delta_{11}\Delta_{21}k_{1} + \Delta_{12}\Delta_{22}k_{2} \\ a_{ii}k_{i} = \displaystyle \sum_{i=1}^{2} a_{ii}k_{i} = a_{11}k_{1} + a_{22}k_{2} \end{array} \right. \]
この剛性行列に現れる、係数 $\Delta_{ij}$、$a_{ij}$ は以下の通りである。
\[\hspace{2em} \begin{array}{lll} 2\Delta_{1_{i}} &=& l_{i}(y_{31}+y_{41}) - m_{i}(x_{31}+x_{41}) \\ 2\Delta_{2_{i}} &=& l_{i}(y_{32}+y_{42}) - m_{i}(x_{32}+x_{42}) \\ \end{array} \] \[\hspace{4em} ( x_{ij} = x_{i} - x_{j} \;, \;\;\; y_{ij} = y_{i} - y_{j} ) \] \[\hspace{2em} a_{11} = 0 \;, \;\;\;\; a_{12} = 0 \;, \;\;\;\; a_{21} = 0 \;, \;\;\;\; a_{22} = \frac{L^{2}}{12} \]
（３）塑性化後の剛性行列
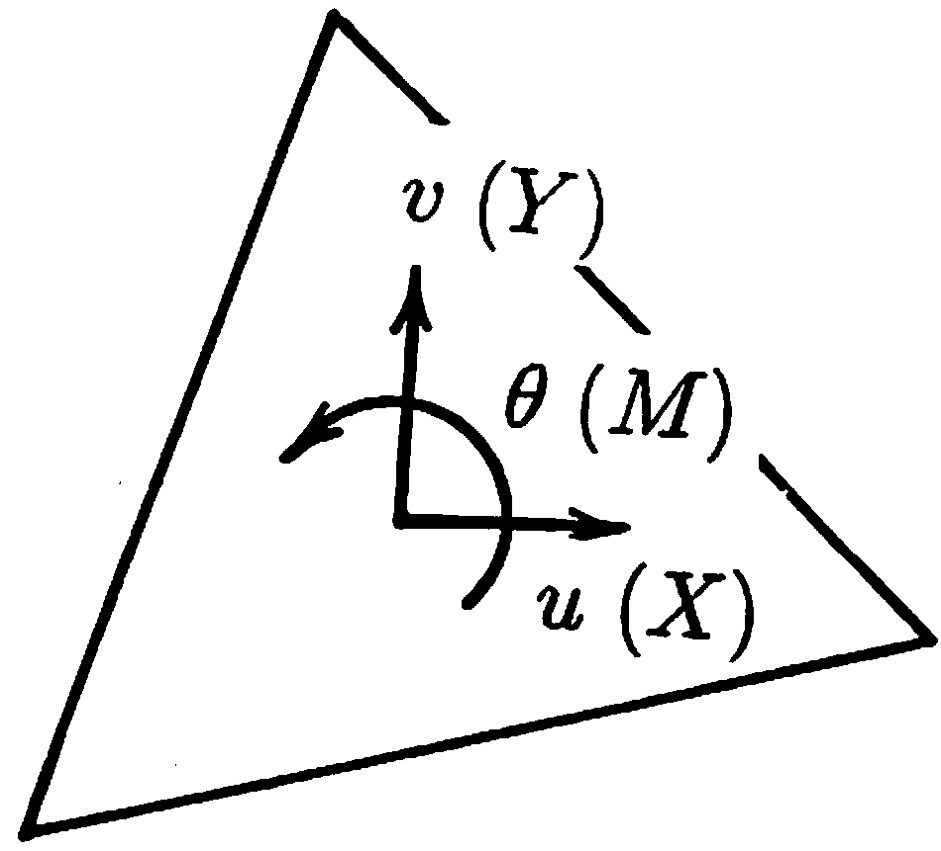
塑性化後ばね行列が
\[{\rm (9.8)}   [k_{ij}] = \left[ \begin{array}{cc} k_{11} & k_{12} \\ k_{21} & k_{22} \end{array} \right] \;\;\;\; ( k_{12} = k_{21}) \]
となった場合の剛性行列を以下に示す。
\[ \begin{array}{lll} \begin{array}{lcl} {K}_{1,1} &=& l_{i}l_{j}k_{ij} \\ {K}_{1,2} &=& l_{i}m_{j}k_{ij} \\ {K}_{1,3} &=& -l_{i}\Delta_{1_{j}}k_{ij} \\ {K}_{1,4} &=& -{K}_{1,1} \\ {K}_{1,5} &=& -{K}_{1,2} \\ {K}_{1,6} &=& l_{i}\Delta_{2_{j}}k_{ij} \end{array} \;\;\;\;\; &\begin{array}{lcl} {K}_{2,2} &=& m_{i}m_{j}k_{ij} \\ {K}_{2,3} &=& -m_{i}\Delta_{1_{j}}k_{ij} \\ {K}_{2,4} &=& -{K}_{1,2} \\ {K}_{2,5} &=& -{K}_{2,2} \\ {K}_{2,6} &=& m_{i}\Delta_{2_{j}}k_{ij} \\ & & \end{array} \;\;\;\;\; &\begin{array}{lll} {K}_{3,3} &=& \Delta_{1_{i}}\Delta_{1_{j}}k_{ij} + a_{ij}k_{ij} \\ {K}_{3,4} &=&-{K}_{1,3} \\ {K}_{3,5} &=&-{K}_{2,3} \\ {K}_{3,6} &=&-\Delta_{1_{i}}\Delta_{2_{j}}k_{ij} - a_{ij}k_{ij} \\ & & \\ & & \end{array} \\ \\ \begin{array}{lcrl} {K}_{4,4} &=& \!\!&\!\!{K}_{1,1} \\ {K}_{4,5} &=& \!\!&\!\!{K}_{1,2} \\ {K}_{4,6} &=& -\!\!&\!\!{K}_{1,6} \end{array} \;\;\;\;\; &\begin{array}{lcrl} {K}_{5,5} &=& \!\!&\!\!{K}_{2,2} \\ {K}_{5,6} &=& -\!\!&\!\!{K}_{2,6} \\ & & & \end{array} \;\;\;\;\; &\begin{array}{lll} {K}_{6,6} &=& \Delta_{2_{i}}\Delta_{2_{j}}k_{ij} + a_{ij}k_{ij} \\ & & \\ & & \end{array} \end{array} \] \[ ( \times L ) \]
記号および添字の関係は、これまでと同一であり、添字については以下のような省略を行っている。
\[{\rm (9.9)}   l_{i}m_{j}k_{ij} = \displaystyle \sum_{i=1}^{2} \sum_{j=1}^{2} l_{i}m_{j}k_{ij} \]

９－３　面外変形平面要素の剛性行列

（１）面外変形平面要素の剛性行列における各成分の被積分項
 図9.2に示すような要素重心の剛体変位ならびに外力の記号を用いると自由度ならびに外力項は以下のようになる。
 
$\hspace{0em}$図9.2　面外変形平面要素の自由度
\[ \boldsymbol{u} = ( w_{1} \;, \;\; \theta_{1} \;, \;\; \phi_{1} \;, \;\; w_{2} \;, \;\; \theta_{2} \;, \;\; \phi_{2} ) \;, \;\;\;\;\; \boldsymbol{F} = ( W_{1} \;, \;\; L_{1} \;, \;\; M_{1} \;, \;\; W_{2} \;, \;\; L_{2} \;, \;\; M_{2} ) \]
 この関係を前提として、３次元の剛性行列における各成分の被積分項を面外変形平面要素用に変形すると以下の式が得られる。
\[ \begin{array}{lcl} k_{1,1} &=& \;\;\; k_{2} \\ k_{1,2} &=& \;\;\; (y-y_{1})k_{2} \\ k_{1,3} &=&- (x-x_{1})k_{2} \\ k_{1,4} &=&- k_{1,1} \\ k_{1,5} &=&- (y-y_{2})k_{2} \\ k_{1,6} &=& \;\;\; (x-x_{2})k_{2} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{2,2} &=& \;\;\; (m_{1}z)^{2}k_{1} + (y-y_{1})^{2}k_{2} + (m_{3}z)^{2}k_{3} \\ k_{2,3} &=&- m_{1}l_{1}z^{2}k_{1} - (y-y_{1})(x-x_{1})k_{2} - m_{3}l_{3}z^{2}k_{3} \\ k_{2,4} &=&- k_{1,2} \\ k_{2,5} &=& - (m_{1}z)^{2}k_{1} - (y-y_{1})(y-y_{2})k_{2} - (m_{3}z)^2k_{3} \\ k_{2,6} &=& \;\;\; m_{1}l_{1}z^{2}k_{1} + (y-y_{1})(x-x_{2})k_{2} + m_{3}l_{3}z^2k_{3} \\ & & \end{array} \] \[ \begin{array}{lcl} k_{3,3} &=& \;\;\; (l_{1}z)^{2}k_{1} + (x-x_{1})^{2}k_{2} + (l_{3}z)^{2}k_{3} \\ k_{3,4} &=&- k_{1,3} \\ k_{3,5} &=& \;\;\; l_{1}m_{1}z^{2}k_{1} + (x-x_{1})(y-y_{2})k_{2} + l_{3}m_{3}z^2k_{3} \\ k_{3,6} &=&- (l_{1}z)^{2}k_{1} - (x-x_{1})(x-x_{2})k_{2} - (l_{3}z)^2k_{3} \end{array} \;\;\;\;\; \begin{array}{lcrl} k_{4,4} &=& \!\!&\!\!k_{1,1} \\ k_{4,5} &=&- \!\!&\!\!k_{1,5} \\ k_{4,6} &=&- \!\!&\!\!k_{1,6} \\ & & & \end{array} \] \[ \begin{array}{lcl} k_{5,5} &=& \;\;\; (m_{1}z)^{2}k_{1} + (y-y_{2})^{2}k_{2} + (m_{3}z)^{2}k_{3} \\ k_{5,6} &=& - m_{1}l_{1}z^{2}k_{1} - (y-y_{2})(x-x_{2})k_{2} - m_{3}l_{3}z^{2}k_{3}\\ \end{array} \] \[ \begin{array}{lcl} k_{6,6} &=& \;\;\; (l_{1}z)^{2}k_{1} + (x-x_{2})^{2}k_{2} + (l_{3}z)^{2}k_{3} \end{array} \]
（２）面外変形平面要素の剛性行列
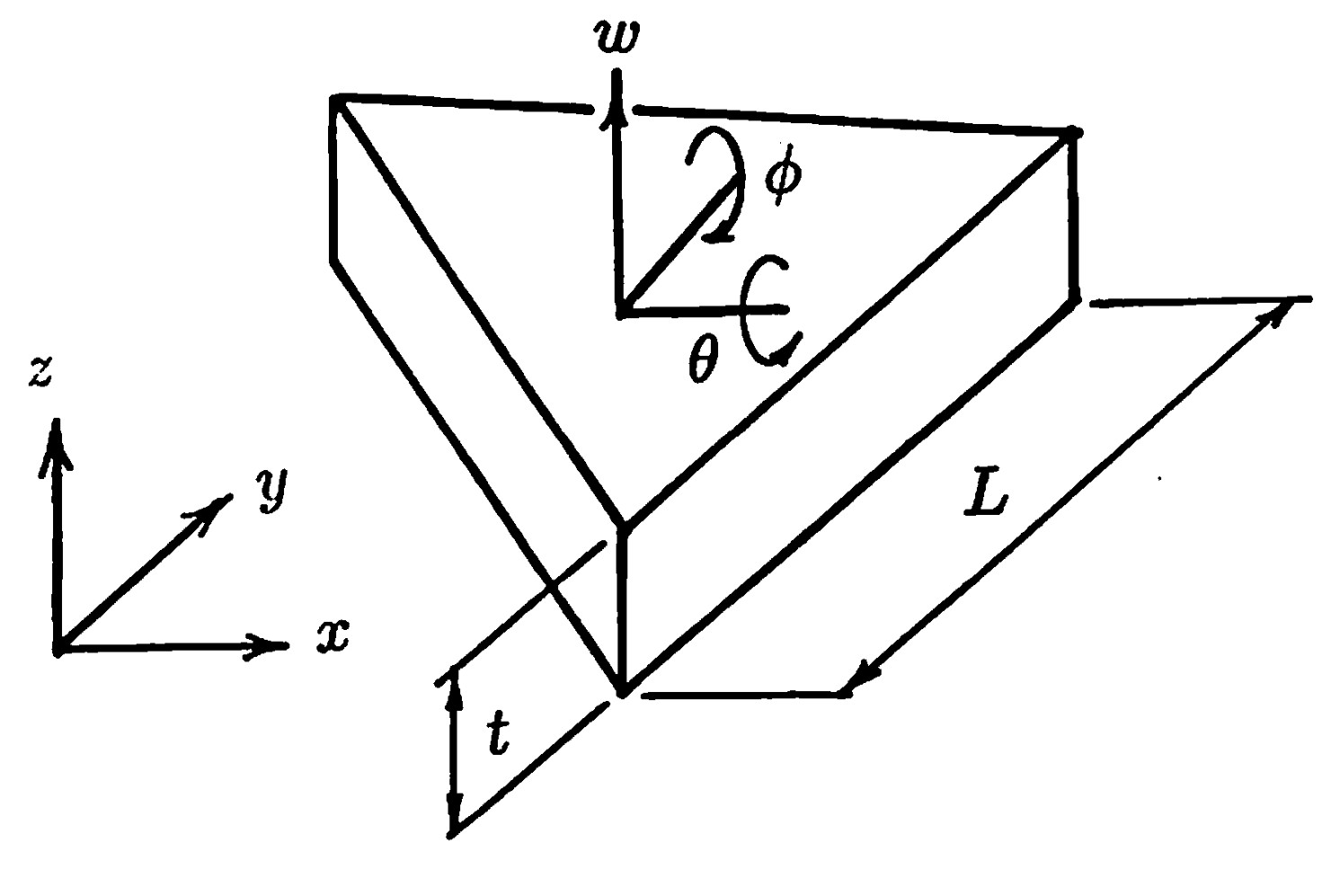
現を簡単にするため、方向余弦の記号を以下のように整理する。
\[\hspace{2em} l_{1} = -m_{3} = l \;, \;\;\; m_{1} = l_{3} = m \]
ここで、$l$、$m$ は以下の通りである。
\[\hspace{2em} l = \frac{x_{43}}{L} \;, \;\;\;\; m = \frac{y_{43}}{L} \] \[\hspace{2em} L = \sqrt{x_{43}^{2}+y_{43}^{2}} \;, \;\;\;\; A = Lt \]
ただし、図に示すよう、$t$ は接触平面の板厚、$A$ は接触面積を表すものとする。
 この関係を用いることで、積分後の要素剛性行列が以下のように得られる。
\[ \begin{array}{lcl} K_{1,1} &=& \;\;\; k_{G} \\ K_{1,2} &=& \;\;\; \Delta_{12}k_{G} \\ K_{1,3} &=& - \Delta_{11}k_{G} \\ K_{1,4} &=& - K_{1,1} \\ K_{1,5} &=& - \Delta_{22}k_{G} \\ K_{1,6} &=& \;\;\; \Delta_{21}k_{G} \end{array} \;\;\;\;\; \begin{array}{lcl} K_{2,2} &=& \;\;\; m^{2}k_{J} + l^{2}k_{M} + \Delta_{12}^2k_{G} \\ K_{2,3} &=& - lmk_{J} + lmk_{M} - \Delta_{12}\Delta_{11}k_{G} \\ K_{2,4} &=& - K_{1,2} \\ K_{2,5} &=& - m^{2}k_{J} - l^{2}k_{M} - \Delta_{12}\Delta_{22}k_{G} \\ K_{2,6} &=& \;\;\; lmk_{J} - lmk_{M} + \Delta_{12}\Delta_{21}k_{G} \\ & & \end{array} \] \[ \begin{array}{lcl} K_{3,3} &=& \;\;\; l^{2}k_{J} + m^{2}k_{M} + \Delta_{11}^2k_{G} \\ K_{3,4} &=& - K_{1,3} \\ K_{3,5} &=& \;\;\; lmk_{J} - lmk_{M} + \Delta_{11}\Delta_{22}k_{G} \\ K_{3,6} &=& - l^{2}k_{J} - m^{2}k_{M} - \Delta_{11}\Delta_{21}k_{G} \end{array} \;\;\;\;\; \begin{array}{lcrl} K_{4,4} &=& \!\!&\!\!K_{1,1} \\ K_{4,5} &=& -\!\!&\!\!K_{1,5} \\ K_{4,6} &=& -\!\!&\!\!K_{1,6} \\ & & & \end{array} \;\;\;\;\; \] \[ \begin{array}{lcl} K_{5,5} &=& \;\;\; m^{2}k_{J} + l^{2}k_{M} + \Delta_{22}^2k_{G} \\ K_{5,6} &=& - lmk_{J} + lmk_{M} - \Delta_{22}\Delta_{21}k_{G} \end{array} \;\;\; \begin{array}{lcl} K_{6,6} &=& \;\;\; l^{2}k_{J} + m^{2}k_{M} + \Delta_{21}^2k_{G} \\ & & \end{array} \]
この剛性行列に現れる係数 $\Delta_{ij}$ は以下の示す通りである。
\[\hspace{2em} \begin{array}{lcl} 2\Delta_{11} &=& x_{31}+x_{41} \\ 2\Delta_{21} &=& x_{32}+x_{42} \end{array} \;\;\;\;\; \begin{array}{lcl} 2\Delta_{12} &=& y_{31}+y_{41} \\ 2\Delta_{22} &=& y_{32}+y_{42} \\ \end{array} \] \[\hspace{4em} ( x_{ij} = x_{i} - x_{j} \;, \;\;\; y_{ij} = y_{i} - y_{j} ) \]
また、ばね定数については、接触断面の断面２次モーメント $(I_x, I_y)$ ならびに、断面２次極モーメント $(I_p)
\[\hspace{2em} I_{x} = \frac{Lt^{3}}{12} \;, \;\;\; I_{y} = \frac{L^{3}t}{12} \;, \;\;\; I_{p} = I_{x} + I_{y} \]
を用い、以下のように定義する。
\[ k_{G} = Ak_{s} \;, \;\;\; k_{J} = I_{p}k_{s} \;, \;\;\; k_{M} = I_{x}k_{n} \;\;\;\;\; ( k_{s \overline{x}} = k_{s \overline{y}} = k_{s} ) \]

９－４　軸対称要素の剛性行列

（１）軸対称要素の剛性行列における各成分の被積分項
 軸対称要素の剛性行列は9.2節で示した面内変形平面要素の剛性行列に以下に示す円周方向のエネルギー
\[\hspace{2em} \int_{l_{34}} \frac{1}{r^{2}} \widehat{\boldsymbol{B}}_{i}^{t} \overline{E} \widehat{\boldsymbol{B}}_{i} dS \]
による成分を追加することで簡単に誘導することができる。
 いま、における被積分項を上付きの￣で表すと、軸対称要素の剛性行列における被積分項は以下のように求められる。
\[ \begin{array}{lcl} k_{1,1} &=& \overline{k}_{1,1} + k_{\theta} \\ k_{1,2} &=& \overline{k}_{1,2} \\ k_{1,3} &=& \overline{k}_{1,3} + (y-y_{1})k_{\theta} \\ k_{1,4} &=& \overline{k}_{1,4} + k_{\theta} \\ k_{1,5} &=& \overline{k}_{1,5} \\ k_{1,6} &=& \overline{k}_{1,6} + (y-y_{2})k_{\theta} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{2,2} &=& \overline{k}_{2,2} \\ k_{2,3} &=& \overline{k}_{2,3} \\ k_{2,4} &=& \overline{k}_{2,4} \\ k_{2,5} &=& \overline{k}_{2,5} \\ k_{2,6} &=& \overline{k}_{2,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{3,3} &=& \overline{k}_{3,3} + (y-y_{1})^{2}k_{\theta} \\ k_{3,4} &=& \overline{k}_{3,4} + (y-y_{1})k_{\theta} \\ k_{3,5} &=& \overline{k}_{3,5} \\ k_{3,6} &=& \overline{k}_{3,6} + (y-y_{1})(y-y_{2})k_{\theta} \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} k_{4,4} &=& \overline{k}_{4,4} + k_{\theta} \\ k_{4,5} &=& \overline{k}_{4,5} \\ k_{4,6} &=& \overline{k}_{4,6} + (y-y_{2})k_{\theta} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{5,5} &=& \overline{k}_{5,5} \\ k_{5,6} &=& \overline{k}_{5,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{6,6} &=& \overline{k}_{6,6} + (y-y_{2})^{2}k_{\theta} \\ & & \\ & & \end{array} \]
ただし、$k_{\theta}$ は
\[\hspace{2em} k_{\theta} = \frac{\overline{E}h}{4r^{2}} \]
であり、それぞれの記号の示す意味は以下の通りである。
\[\hspace{2em} \overline{E} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)} \;, \;\;\; h = \frac{h_{1}+h_{2}}{2} \;, \;\;\; r = \frac{r_{3}+r_{4}}{2} \]
（２）軸対称要素の剛性行列
 9.4(1)節に示した被積分項を円周方向に積分を実行した後の軸対称要素の剛性行列を以下に示す。
\[ \begin{array}{lcl} K_{1,1} &=& \overline{K}_{1,1} + Lk_{\theta} \\ K_{1,2} &=& \overline{K}_{1,2} \\ K_{1,3} &=& \overline{K}_{1,3} + \Delta_{1}Lk_{\theta} \\ K_{1,4} &=& \overline{K}_{1,4} + Lk_{\theta} \\ K_{1,5} &=& \overline{K}_{1,5} \\ K_{1,6} &=& \overline{K}_{1,6} + \Delta_{2}Lk_{\theta} \end{array} \;\;\;\;\; \begin{array}{lcl} K_{2,2} &=& \overline{K}_{2,2} \\ K_{2,3} &=& \overline{K}_{2,3} \\ K_{2,4} &=& \overline{K}_{2,4} \\ K_{2,5} &=& \overline{K}_{2,5} \\ K_{2,6} &=& \overline{K}_{2,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} K_{3,3} &=& \overline{K}_{3,3} + (\Delta_{1}^{2} + y_{35}^{2}/12)Lk_{\theta} \\ K_{3,4} &=& \overline{K}_{3,4} + \Delta_{1}Lk_{\theta} \\ K_{3,5} &=& \overline{K}_{3,5} \\ K_{3,6} &=& \overline{K}_{3,6} + (\Delta_{1}\Delta_{2} + y_{35}^{2}/12)Lk_{\theta} \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} K_{4,4} &=& \overline{K}_{4,4} + Lk_{\theta} \\ K_{4,5} &=& \overline{K}_{4,5} \\ K_{4,6} &=& \overline{K}_{4,6} + \Delta_{2}Lk_{\theta} \end{array} \;\;\;\;\; \begin{array}{lcl} K_{5,5} &=& \overline{K}_{5,5} \\ K_{5,6} &=& \overline{K}_{5,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} K_{6,6} &=& \overline{K}_{6,6} + (\Delta_{2}^{2} + y_{35}^{2}/12)Lk_{\theta} \\ & & \\ & & \end{array} \]
各記号については式(9.1)と同一な関係を用いている。

９－５　３次元梁要素の剛性行列

（１）３次元梁要素の剛性行列における各成分の被積分項
 9.1節で示した一般的な３次元要素の剛性行列における各成分の被積分項に1.2(5)節で示した方向余弦の特殊性を導入すると３次元梁要素の被積分項が以下のように求められる。
\[ \begin{array}{lcl} k_{1,1} &=& \;\;\; k_{1} \\ k_{1,2} &=& \;\;\; 0 \\ k_{1,3} &=& \;\;\; 0 \\ k_{1,4} &=& \;\;\; 0 \\ k_{1,5} &=& \;\;\; \frac{L_{1}}{2}k_{1} \\ k_{1,6} &=& - yk_{1} \\ k_{1,7} &=& - k_{1,1} \\ k_{1,8} &=& - k_{1,2} \\ k_{1,9} &=& - k_{1,3} \\ k_{1,10} &=& \;\;\; 0 \\ k_{1,11} &=& \;\;\; \frac{L_{2}}{2}k_{1} \\ k_{1,12} &=& - k_{1,6} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{2,2} &=& \;\;\; k_{2} \\ k_{2,3} &=& \;\;\; 0 \\ k_{2,4} &=& - \frac{L_{1}}{2}k_{2} \\ k_{2,5} &=& \;\;\; 0 \\ k_{2,6} &=& \;\;\; xk_{2} \\ k_{2,7} &=& - k_{1,2} \\ k_{2,8} &=& - k_{2,2} \\ k_{2,9} &=& - k_{2,3} \\ k_{2,10} &=& - \frac{L_{2}}{2}k_{2} \\ k_{2,11} &=& \;\;\; 0 \\ k_{2,12} &=& - k_{2,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{3,3} &=& \;\;\; k_{3} \\ k_{3,4} &=& \;\;\; yk_{3} \\ k_{3,5} &=&- xk_{3} \\ k_{3,6} &=& \;\;\; 0 \\ k_{3,7} &=& - k_{1,3} \\ k_{3,8} &=& - k_{2,3} \\ k_{3,9} &=& - k_{3,3} \\ k_{3,10} &=& - k_{3,4} \\ k_{3,11} &=& - k_{3,5} \\ k_{3,12} &=& - k_{3,6} \\ & & \\ & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{4,4} &=& \;\;\; (\frac{L_{1}}{2})^{2}k_{2} + y^{2}k_{3} \\ k_{4,5} &=& - xyk_{3} \\ k_{4,6} &=& - \frac{L_{1}}{2}k_{2} \\ k_{4,7} &=& - k_{1,4} \\ k_{4,8} &=& - k_{2,4} \\ k_{4,9} &=& - k_{3,4} \\ k_{4,10} &=& \;\;\; \frac{L_{1}}{2}\frac{L_{2}}{2}k_{2} - y^{2}k_{3} \\ k_{4,11} &=& - k_{4,5} \\ k_{4,12} &=& - k_{4,6} \\ & & \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} k_{5,5} &=& \;\;\; (\frac{L_{1}}{2})^{2}k_{1} + x^{2}k_{3} \\ k_{5,6} &=& - \frac{L_{1}}{2}yk_{1} \\ k_{5,7} &=& - k_{1,5} \\ k_{5,8} &=& - k_{2,5} \\ k_{5,9} &=& - k_{3,5} \\ k_{5,10} &=& \;\;\; xyk_{3} \\ k_{5,11} &=& \;\;\; \frac{L_{1}}{2}\frac{L_{2}}{2}k_{1} - x^{2}k_{3} \\ k_{5,12} &=& - k_{5,6} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{6,6} &=& \;\;\; y^{2}k_{1} + x^{2}k_{2} \\ k_{6,7} &=& - k_{1,6} \\ k_{6,8} &=& - k_{2,6} \\ k_{6,9} &=& - k_{3,6} \\ k_{6,10} &=& - \frac{L_{2}}{2}xk_{2} \\ k_{6,11} &=& - \frac{L_{2}}{2}yk_{2} \\ k_{6,12} &=& - k_{6,6} \\ & & \end{array} \;\;\;\;\; \begin{array}{lcrl} k_{7,7} &=& \!\!&\!\!k_{1,1} \\ k_{7,8} &=& \!\!&\!\!k_{1,2} \\ k_{7,9} &=& \!\!&\!\!k_{1,3} \\ k_{7,10} &=& -\!\!&\!\!k_{1,10} \\ k_{7,11} &=& -\!\!&\!\!k_{1,11} \\ k_{7,12} &=& -\!\!&\!\!k_{1,12} \\ & & \\ & & \end{array} \] \[ \begin{array}{lcrl} k_{8,8} &=& \!\!&\!\!k_{2,2} \\ k_{8,9} &=& \!\!&\!\!k_{2,3} \\ k_{8,10} &=& -\!\!&\!\!k_{2,10} \\ k_{8,11} &=& -\!\!&\!\!k_{2,11} \\ k_{8,12} &=& -\!\!&\!\!k_{2,12} \end{array} \;\;\;\;\; \begin{array}{lcrl} k_{9,9} &=& \!\!&\!\!k_{3,3} \\ k_{9,10} &=& -\!\!&\!\!k_{3,10} \\ k_{9,11} &=& -\!\!&\!\!k_{3,11} \\ k_{9,12} &=& -\!\!&\!\!k_{3,12} \\ & & & \end{array} \;\;\;\;\; \begin{array}{lcl} k_{10,10} &=& \;\;\; (\frac{L_{2}}{2})^{2}k_{2} + y^{2}k_{3} \\ k_{10,11} &=& - xyk_{3} \\ k_{10,12} &=& \;\;\; \frac{L_{2}}{2}xk_{2} \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} k_{11,11} &=& \;\;\; (\frac{L_{2}}{2})^{2}k_{1} + x^{2}k_{3} \\ k_{11,12} &=& \;\;\; \frac{L_{2}}{2}yk_{2} \end{array} \;\;\;\;\; \begin{array}{lcl} k_{12,12} &=& \;\;\; y^{2}k_{1} + x^{2}k_{2} \\ & & \end{array} \] ここで、記号については9.1節と同様であり、$L_1$、$L_2$ は各部材の長さを表している。
（２）３次元梁要素の剛性行列
 9.5(1)節で示した被積分項の積分を実行し、剛性行列を陽な形で求めるためには接触断面形状に応じた積分を予め求めておかなければならない。梁要素の場合、断面の諸量により以下のように簡潔にこの積分を表現することができる。
\[ \int_{A}dA = A \;, \;\;\; \int_{A}y^{2}dA = I_{x} \;, \;\;\; \int_{A}x^{2}dA = I_{y} \;, \;\;\; \int_{A}xydA = I_{xy} \;, \;\;\; I_{p} = I_{x} + I_{y} \] \[ \int_{A}xdA = \int_{A}ydA = 0 \] ここで、$A$ は接触面の断面積、$I_x$、$I_y$ はそれぞれの軸に対する断面２次モーメント、 $I_p$ は断面極モーメント、$I_{xy}$ は断面相乗モーメントを意味している。また、$z$ 軸が部材の中立軸を通り、かつ図心軸と一致する場合、$x$、$y$ に関する断面１次モーメントは0となる。これらの関係を用い、３次元梁要素の剛性行列を求めると以下のようになる。
\[ \begin{array}{lcl} K_{1,1} &=& \;\;\; GA \\ K_{1,2} &=& \;\;\; 0 \\ K_{1,3} &=& \;\;\; 0 \\ K_{1,4} &=& \;\;\; 0 \\ K_{1,5} &=& \;\;\; \frac{L_{1}}{2}GA \\ K_{1,6} &=& \;\;\; 0 \\ K_{1,7} &=& - GA \\ K_{1,8} &=& \;\;\; 0 \\ K_{1,9} &=& \;\;\; 0 \\ K_{1,10} &=& \;\;\; 0 \\ K_{1,11} &=& \;\;\; \frac{L_{2}}{2}GA \\ K_{1,12} &=& \;\;\; 0 \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{2,2} &=& \;\;\; GA \\ K_{2,3} &=& \;\;\; 0 \\ K_{2,4} &=& - \frac{L_{2}}{2}GA \\ K_{2,5} &=& \;\;\; 0 \\ K_{2,6} &=& \;\;\; 0 \\ K_{2,7} &=& \;\;\; 0 \\ K_{2,8} &=& - GA \\ K_{2,9} &=& \;\;\; 0 \\ K_{2,10} &=& - \frac{L_{2}}{2}GA \\ K_{2,11} &=& \;\;\; 0 \\ K_{2,12} &=& \;\;\; 0 \\ & & \end{array} \;\;\;\;\;\;\; \begin{array}{lcl} K_{3,3} &=& \;\;\; EA \\ K_{3,4} &=& \;\;\; 0 \\ K_{3,5} &=& \;\;\; 0 \\ K_{3,6} &=& \;\;\; 0 \\ K_{3,7} &=& \;\;\; 0 \\ K_{3,8} &=& \;\;\; 0 \\ K_{3,9} &=& - EA \\ K_{3,10} &=& \;\;\; 0 \\ K_{3,11} &=& \;\;\; 0 \\ K_{3,12} &=& \;\;\; 0 \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} K_{4,4} &=& \;\;\; (\frac{L_{1}}{2})^{2}GA + EI_{x} \\ K_{4,5} &=& - EI_{xy} \\ K_{4,6} &=& \;\;\; 0 \\ K_{4,7} &=& \;\;\; 0 \\ K_{4,8} &=& \;\;\; \frac{L_{2}}{2}GA \\ K_{4,9} &=& \;\;\; 0 \\ K_{4,10} &=& \;\;\; \frac{L_{1}}{2}\frac{L_{2}}{2}GA - EI_{x} \\ K_{4,11} &=& \;\;\; EI_{xy} \\ K_{4,12} &=& \;\;\; 0 \end{array} \;\;\;\; \begin{array}{lcl} K_{5,5} &=& \;\;\; (\frac{L_{1}}{2})^{2}GA + EI_{y} \\ K_{5,6} &=& \;\;\; 0 \\ K_{5,7} &=& - \frac{L_{1}}{2}GA \\ K_{5,8} &=& \;\;\; 0 \\ K_{5,9} &=& \;\;\; 0 \\ K_{5,10} &=& \;\;\; EI_{xy} \\ K_{5,11} &=& \;\;\; \frac{L_{1}}{2}\frac{L_{2}}{2}GA - EI_{y} \\ K_{5,12} &=& \;\;\; 0 \\ & & \end{array} \;\;\;\; \begin{array}{lcl} K_{6,6} &=& \;\;\; I_{p}G \\ K_{6,7} &=& \;\;\; 0 \\ K_{6,8} &=& \;\;\; 0 \\ K_{6,9} &=& \;\;\; 0 \\ K_{6,10} &=& \;\;\; 0 \\ K_{6,11} &=& \;\;\; 0 \\ K_{6,12} &=& - I_{p}G \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} K_{7,7} &=& \;\;\; GA \\ K_{7,8} &=& \;\;\; 0 \\ K_{7,9} &=& \;\;\; 0 \\ K_{7,10} &=& \;\;\; 0 \\ K_{7,11} &=& - \frac{L_{2}}{2}GA \\ K_{7,12} &=& \;\;\; 0 \end{array} \;\;\;\; \begin{array}{lcl} K_{8,8} &=& GA \\ K_{8,9} &=& 0 \\ K_{8,10} &=& \frac{L_{2}}{2}GA \\ K_{8,11} &=& 0 \\ K_{8,12} &=& 0 \\ & & \end{array} \;\;\;\; \begin{array}{lcl} K_{9,9} &=& EA \\ K_{9,10} &=& 0 \\ K_{9,11} &=& 0 \\ K_{9,12} &=& 0 \\ & & \\ & & \end{array} \] \[ \begin{array}{lcl} K_{10,10} &=& \;\;\; (\frac{L_{2}}{2})^{2}GA + EI_{x} \\ K_{10,11} &=&- EI_{xy} \\ K_{10,12} &=& \;\;\; 0 \\ \end{array} \;\;\;\; \begin{array}{lcl} K_{11,11} &=& (\frac{L_{2}}{2})^{2}GA + EI_{y} \\ K_{11,12} &=& 0 \\ & & \end{array} \;\;\;\; \begin{array}{lcl} K_{12,12} &=& I_{p}G \\ & & \\ & & \end{array} \] \[ ( \times \;\; 2/(L_{1}+L_{2}) \;\; ) \]

９－６　２次元梁要素の剛性行列

 ２次元梁要素の剛性行列は３次元梁要素の剛性行列を整理することで簡単に得ることができる。ここでは、使用目的毎に３次元梁要素の剛性行列から必要成分を取り出し、剛性行列を作成する。
（１）軸剛性行列
 軸力を受ける梁の剛性行列は３次元梁要素の剛性行列において、$z$ 軸方向の変位 $(w)$ ならびに外力 $(z)$ に該当する項を取り出すことによりより表すことができる。以下に軸剛性行列を示す。
\[ \left\{ \begin{array}{c} Z_{1} \\ Z_{2} \end{array} \right\} = \frac{2}{L} \left[ \begin{array}{rr} EA & -EA \\ -EA & EA \end{array} \right] \left\{ \begin{array}{c} w_{1} \\ w_{2} \end{array} \right\} \;\;\;\;\;\;\; ( L = L_{1} + L_{2} ) \]
ここで、記号の意味は9.5節と同じであり、$L$ は２つの部材長をたしたものである。この結果より、川井モデルの軸剛性に関しては従来の変形法におけるト ラス要素と同一であることがわかる。したがって、自由度の位置から考えると、単純なトラス構造の解析を行う場合には従来の変形法による解析の方が簡単であるが、ロック・ボルトやアンカーを表現するため、川井モデルの平面要素と組み合わせてトラス要素を利用する場合にはここで示した要素を利用した方が都合よい。
（２）せん断変形を考慮した曲げ剛性行列
 図9.3に示すような $z-x$ 平面を考え、変位 $(u, \phi)$、外力 $(X,M)$ に関する項を取り出すことにより、せん断変形を考慮した梁の曲げ剛性行列が得られる。以下にその結果を示す。
 
$\hspace{4em}$図9.3　面内荷重を受ける梁要素の自由度
\[ \left\{ \begin{array}{c} X_{1} \\ M_{1} \\ X_{2} \\ M_{2} \end{array} \right\} = \frac{2}{L} \left[ \begin{array}{cccc} GA & \frac{L_{1}}{2}GA & -GA & \frac{L_{2}}{2}GA \\ & EI_{x} + (\frac{L_{1}}{2})^{2}GA & -\frac{L_{1}}{2}GA & -EI_{x} +\frac{L_{1}L_{2}}{4}GA \\ & & GA & -\frac{L_{2}}{2}GA \\ & sym. & & EI_{x} + (\frac{L_{2}}{2})^{2}GA \end{array} \right] \left\{ \begin{array}{c} u_{1} \\ \phi_{1} \\ u_{2} \\ \phi_{2} \end{array} \right\} \]
 この結果と9.6(1)節の軸剛性を重ね合わせることにより、図9.3 に示す面内変形を前提とした２次元梁要素の関係が以下のように得られる。
\[ \left\{ \begin{array}{c} Z_{1} \\ X_{1} \\ M_{1} \\ Z_{2} \\ X_{2} \\ M_{2} \end{array} \right\} = \frac{2}{L} \left[ \begin{array}{cccccc} EA & 0 & 0 & -EA & 0 & 0 \\ & GA & \frac{L_{1}}{2}GA & 0 & -GA & \frac{L_{2}}{2}GA \\ & & EI_{x} + (\frac{L_{1}}{2})^{2}GA & 0 & -\frac{L_{1}}{2}GA & -EI_{x} +\frac{L_{1}L_{2}}{4}GA \\ & & & EA & 0 & 0\\ & & & & GA & -\frac{L_{2}}{2}GA \\ & & sym. & & & EI_{x} + (\frac{L_{2}}{2})^{2}GA \end{array} \right] \left\{ \begin{array}{c} w_{1} \\ u_{1} \\ \phi_{1} \\ w_{2} \\ u_{2} \\ \phi_{2} \end{array} \right\} \]
川井モデルによる一般的な２次元骨組構造解析ではこの関係を利用するとよい。
（３）ねじり剛性行列
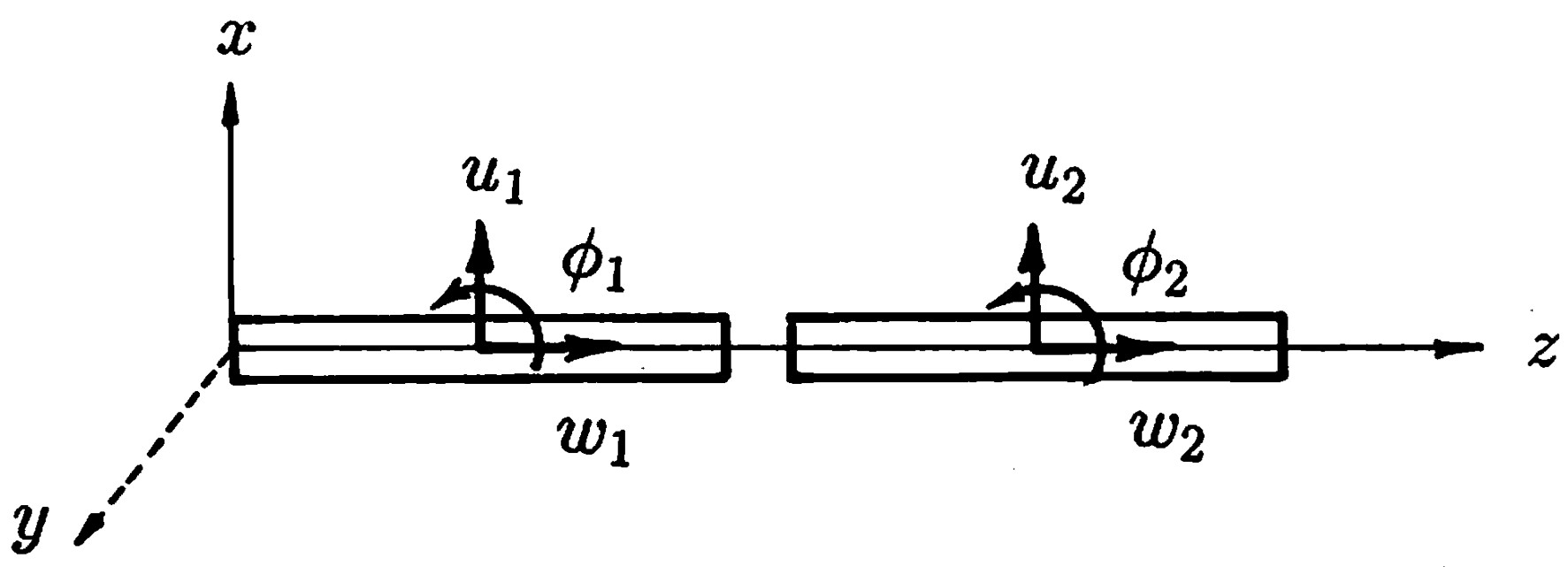
 $z$ 軸に関するねじり剛性行列は $z$ 軸回りの回転変位 $(\chi)$ とねじりモーメントに関する項を取り代ことにより以下のように求められる。
\[ \left\{ \begin{array}{c} N_{1} \\ N_{2} \end{array} \right\} = \frac{2}{L} \left[ \begin{array}{rr} GI_{p} & -GI_{p} \\ -GI_{p} & GI_{p} \end{array} \right] \left\{ \begin{array}{c} \chi_{1} \\ \chi_{2} \end{array} \right\} \]
 面外荷重を受ける一般的な格子構造の解析を行う場合には図9.4に示すような $z-y$ 平面を考え、このねじり剛性とせん断変形を考慮した曲げ剛性を重ね合わせることで以下のように誘導することができる。
 
$\hspace{4em}$図9.4　面外荷重を受ける梁要素に自由度
\[ \left\{ \begin{array}{c} N_{1} \\ X_{1} \\ M_{1} \\ N_{2} \\ X_{2} \\ M_{2} \end{array} \right\} = \frac{2}{L} \left[ \begin{array}{cccccc} GI_{p} & 0 & 0 & -GI_{p} & 0 & 0 \\ & GA & \frac{L_{1}}{2}GA & 0 & -GA & \frac{L_{2}}{2}GA \\ & & EI_{x} + (\frac{L_{1}}{2})^{2}GA & 0 & -\frac{L_{1}}{2}GA & -EI_{x} +\frac{L_{1}L_{2}}{4}GA \\ & & & GI_{p} & 0 & 0\\ & & & & GA & -\frac{L_{2}}{2}GA \\ & & sym. & & & EI_{x} + (\frac{L_{2}}{2})^{2}GA \end{array} \right] \left\{ \begin{array}{c} \chi_{1} \\ u_{1} \\ \phi_{1} \\ \chi_{2} \\ u_{2} \\ \phi_{2} \end{array} \right\} \]

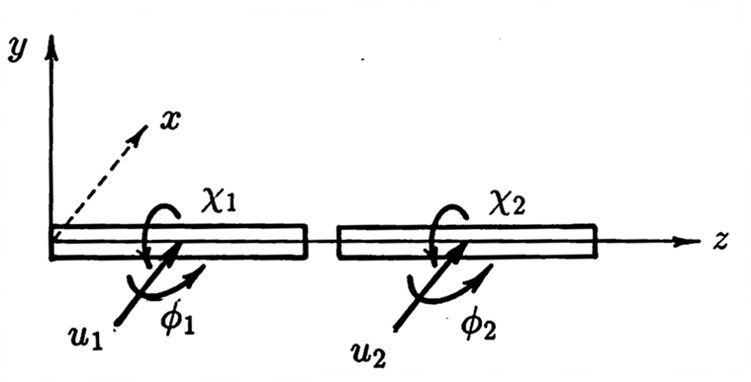
９－７　塑性化後の構成式

 1章の式(1.58)を用いて誘導した塑性化後の構成式と式(1.56)をにより導いた入を以下に示す。
（１）トレスカの条件
(3次元要素の場合）
\[ \boldsymbol{D}^{p} = \boldsymbol{D}^{e} - \boldsymbol{S} \] \[ \boldsymbol{D}^{e} = \left[ \begin{array}{ccc} k_{s} & 0 & 0 \\ 0 & k_{s} & 0 \\ 0 & 0 & k_{n} \end{array} \right] \;, \;\;\; \boldsymbol{S} = \frac{k_{s}}{ \tau_{s \overline{x}}^{2} + \tau_{s \overline{y}}^{2} } \left[ \begin{array}{ccc} \tau_{s \overline{x}}^{2} & \tau_{s \overline{x}} \tau_{s \overline{y}} & 0 \\ & \tau_{s \overline{y}}^{2} & 0 \\ sym. & & 0 \end{array} \right] \] \[ \lambda = \frac{1}{ 2( \tau_{s \overline{x}}^{2} + \tau_{s \overline{y}}^{2} ) } ( \tau_{s \overline{x}} \cdot \Delta \gamma_{\overline{x}} + \tau_{s \overline{y}} \cdot \Delta \gamma_{\overline{y}} ) \]
(2次元要素の場合）
\[ \boldsymbol{D}^{e} = \left[ \begin{array}{cc} k_{n} & 0 \\ 0 & k_{s} \end{array} \right] \;, \;\;\; \boldsymbol{S} = \left[ \begin{array}{ccc} 0 & 0 \\ 0 & k_{s} \end{array} \right] \] \[ \lambda = \frac{ \Delta \gamma }{ 2 \tau } \]
（２）モール・クーロンの条件 (3次元要素の場合）
(3次元要素の場合）
\[ \boldsymbol{D}^{p} = \boldsymbol{D}^{e} - \boldsymbol{S} \] \[ \boldsymbol{D}^{e} = \left[ \begin{array}{ccc} k_{s} & 0 & 0 \\ 0 & k_{s} & 0 \\ 0 & 0 & k_{n} \end{array} \right] \;, \;\;\; \boldsymbol{S} = \frac{1}{ F } \left[ \begin{array}{ccc} \tau_{s \overline{x}}^{2} k_{s}^{2} & \tau_{s \overline{x}} \tau_{s \overline{y}} k_{s}^{2} & \tau_{s \overline{x}} ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{s}k_{n} \\ & \tau_{s \overline{y}}^{2} k_{s}^{2} & \tau_{s \overline{y}} ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{s}k_{n} \\ sym. & & \{ ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{n} \}^{2} \end{array} \right] \] \[ F = \tau_{s \overline{x}}^{2} \cdot k_{s} + \tau_{s \overline{y}}^{2} \cdot k_{s} + \{ ( c- \sigma_{n} \tan \phi ) \tan \phi \}^{2} k_{n} \] \[ \lambda = \frac{1}{2F} \{ \tau_{s \overline{x}} \cdot k_{s} \cdot \Delta \gamma_{\overline{x}} + \tau_{s \overline{y}} \cdot k_{s} \cdot \Delta \gamma_{\overline{y}} + ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{n} \cdot \Delta \epsilon_{n} \} \]
(2次元要素の場合）1
\[ \boldsymbol{D}^{e} = \left[ \begin{array}{cc} k_{n} & 0 \\ 0 & k_{s} \end{array} \right] \;, \;\;\; = \frac{1}{ F } \left[ \begin{array}{cc} \{ ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{n} \}^{2} & \tau ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{s}k_{n} \\ sym. & \tau^{2} k_{s}^{2} \end{array} \right]\boldsymbol{S} \] \[ F = \tau^{2} \cdot k_{s} + \{ ( c- \sigma_{n} \tan \phi ) \tan \phi \}^{2} k_{n} \] \[ \lambda = \frac{1}{2F} \{ \tau \cdot k_{s} \cdot \Delta \gamma + ( c- \sigma_{n} \tan \phi ) \tan \phi \cdot k_{n} \cdot \Delta \epsilon_{n} \} \]
 同様な手順により他の構成式についても誘導することができる。

９－８　質量行列

（１）3次元要素の質量行列
 一般に、川井モデルにおける3次元要素の質量行列 $\boldsymbol{M}$ は以下のように表すことができる。
\[ \boldsymbol{M} = \left[ \begin{array}{cccccc} M_{11} & 0 & 0 & 0 & M_{15} & M_{16} \\ & M_{22} & 0 & M_{24} & 0 & M_{26} \\ & & M_{33} & M_{34} & M_{35} & 0 \\ & & & M_{44} & M_{45} & M_{46} \\ & sym. & & & M_{55} & M_{56} \\ & & & & & M_{66} \end{array} \right] \]
ここで、それぞれの成分は以下に示す通りである。
\[ M_{11} = \frac{\gamma}{g} \int_{v}dv = m \;\;\;\;\;\; M_{15} = \frac{\gamma}{g} \int_{v}(z-z_{G})dv \;\;\;\;\;\; M_{16} = - \frac{\gamma}{g} \int_{v}(y-y_{G})dv \] \[ M_{22} = M_{11} \;\;\;\;\;\; M_{24} = -M_{15} \;\;\;\;\;\; M_{26} = \frac{\gamma}{g} \int_{v}(x-x_{G})dv \] \[ M_{33} = M_{11} \;\;\;\;\;\; M_{34} = -M_{16} \;\;\;\;\;\; M_{35} = -M_{26} \] \[ M_{44} = \frac{\gamma}{g} \int_{v} \{ (y-y_{G})^{2}+(z-z_{G})^{2} \}dv \;\;\;\;\;\; M_{45} =- \frac{\gamma}{g} \int_{v} (x-x_{G})(y-y_{G}) dv \] \[ M_{46} =- \frac{\gamma}{g} \int_{v} (x-x_{G})(z-z_{G}) dv \;\;\;\;\;\; M_{55} = \frac{\gamma}{g} \int_{v} \{ (x-x_{G})^{2}+(z-z_{G})^{2} \}dv \] \[ M_{56} =- \frac{\gamma}{g} \int_{v} (y-y_{G})(z-z_{G}) dv \;\;\;\;\;\; M_{66} = \frac{\gamma}{g} \int_{v} \{ (x-x_{G})^{2}+(y-y_{G})^{2} \}dv \]
 いま、$(x_G, y_G, z_G)$ を要素の重心座標にとれば、上記の関係において
\[ M_{15} = M_{16} = M_{24} = M_{26} = M_{34} = M_{35} = 0 \]
となる。また、座標軸と慣性軸が一致とているなら
\[ M_{45} = M_{46} = M_{56} = 0 I \]
となり、質董行列は以下のように対角行列となる。
\[ \boldsymbol{M} = \left[ \begin{array}{cccccc} M_{11} & 0 & 0 & 0 & 0 & 0 \\ & M_{22} & 0 & 0 & 0 & 0 \\ & & M_{33} & 0 & 0 & 0 \\ & & & M_{44} & 0 & 0 \\ & sym. & & & M_{55} & 0 \\ & & & & & M_{66} \end{array} \right] \]
（２）平面要素の質量行列
 平面要素の質量行列は、3次元要素の質董行列を簡略化することにより、以下のように得られる。
\[ \boldsymbol{M} = \left[ \begin{array}{ccc} M_{11} & 0 & M_{13} \\ & M_{22} & M_{23} \\ sym. & & M_{33} \end{array} \right] \]
ここで、それぞれの成分は以下に示す通りである。
\[ M_{11} = \frac{\gamma}{g} \int_{v}dv = m \;\;\;\;\;\; M_{13} = - \frac{\gamma}{g} \int_{v}(y-y_{G})dv \;\;\;\;\;\; M_{22} = M_{11} \] \[ M_{23} = \frac{\gamma}{g} \int_{v}(x-x_{G})dv \;\;\;\;\;\; M_{33} = \frac{\gamma}{g} \int_{v} \{ (x-x_{G})^{2}+(y-y_{G})^{2} \}dv \]
もし、$(x_G, y_G)$ が要素の重心座標であるなら、先の成分において
\[ M_{13} = M_{23} = 0 \]
となり、以下のように された質量行列が得られる。
\[ \boldsymbol{M} = \left[ \begin{array}{ccc} M_{11} & 0 & 0 \\ & M_{22} & 0 \\ sym. & & M_{33} \end{array} \right] \]
（３） 3次元梁要素の質量行列
 3次元梁要素の質呈行列は一般の3次元要素の特別な場合として以下のように誘導することができる。
\[ \boldsymbol{M} = \left[ \begin{array}{cccccc} M_{11} & 0 & 0 & 0 & 0 & 0 \\ & M_{22} & 0 & 0 & 0 & 0 \\ & & M_{33} & 0 & 0 & 0 \\ & & & M_{44} & 0 & 0 \\ & sym. & & & M_{55} & 0 \\ & & & & & M_{66} \end{array} \right] \]
ここで、各成分は部材の長さを $l$、断面積を $A$ として
\[ M_{11} = M_{22} = M_{33} = m = \rho A l \;\;\;\;\; M_{44} = M_{55} = \frac{m}{12}l^{2} = \frac{1}{12} \rho A l^{3} \] \[ M_{66} = \rho J l \;\;\; (J=I_{x}+I_{y}) \]
となる。ただし、$\rho$ は密度を表すものとする。
（４）2次元梁要素の質量行列
 2次元梁要素の質量行列は3次元梁要素の質量行列から以下のように導くことができる。
\[ {\bf M} = \left[ \begin{array}{ccc} M_{11} & 0 & 0 \\ & M_{22} & 0 \\ sym. & & M_{33} \end{array} \right] \]
ここで、$A$ を断面積、$l$ を部材長、$\rho$ を密度とすると、各成分は以下に示す通Iりである。
\[ M_{11} = M_{22} = m = \rho A l \;\;\;\;\;\; M_{33} = \frac{m}{12} l^{2} = \frac{1}{12} \rho A l^{3} \]
 以上の関係は1章において示した座標系に従って誘導したものであり、質量は常に重心において評価するものと考えている。この場合、質量行列は集中質星行列となり、要素単位で作成することができる。