構造物の応力解析を行うとき、その構造物を理想化し、また簡略化して梁要素に近似することが度々ある。この梁要素は通常の骨組構造のみならず、杭や矢板あるいは埋設管などのように地盤を考慮した梁としても多く用いられている。変形モデルの有限要素法により弾性支承上の梁の問題を解く場合、たわみの４階微分方程式に変位の１次関数が含まれるため、剛性行列は指数関数を含む複雑なものとなる。
\[{\rm (8.1)}
EI \frac{d^{4}y}{dx^{4}} + ky = 0
\]
さらに地盤の塑性化を考慮し、微分方程式におけるたわみの関数を複雑にすればするほど解析的に剛性行列を得るのが困難になる。
地盤をHookの法則に従う弾性体とし、地盤反力が梁のたわみに比例するという仮定は初めWinkler により1867年に導入された。この方法で注意しなければいけないことは、Winkler の仮定が地盤を離散型のばねとしていることである。この方法では、一つ一つの地盤ばねを独立に扱うため、
図8.1に示されるように他のばねの影響をまったく受けず、地盤の連続性を無視している。したがって、せん断剛性の大きな構造では現象を正確に捉えた解析になっているとはいいがたい。しかし、工学的な観点からすると実用性があり、十分注意を払えばその利用価値は依然として高いものがある。ここでは、このWinkler の仮定に従った川井モデルの梁要素に対する定式化について説明する。
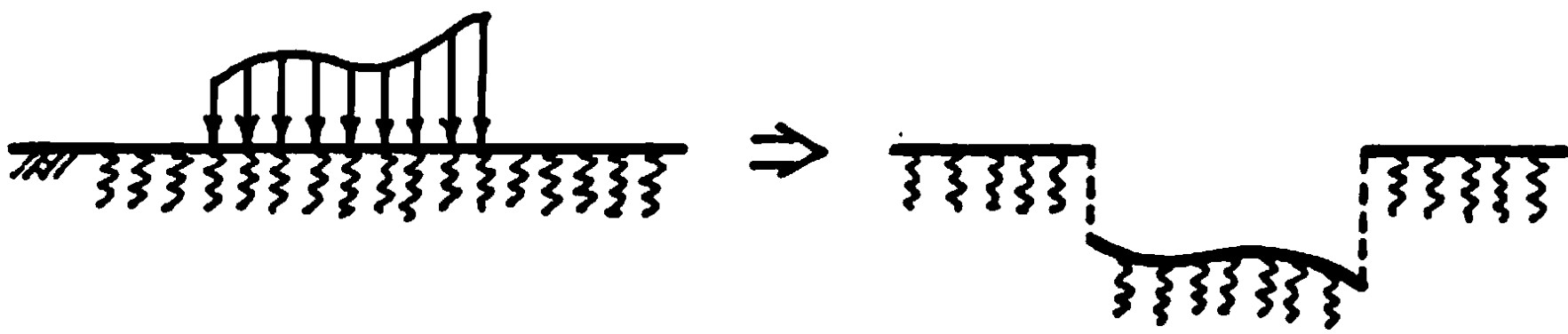
$\hspace{4em}$図8.1 離散型ばねの変形モード
先にも述べたように、地盤を考慮した梁要素の剛性行列は複雑なものとなる。これを避けるため、ばね支点を用いる方法も考えられるが、ばね支点の間隔により大幅に解が異なるため、実用的に利用する場合は注意が必要である。一方、川井モデルの梁要素では剛体変位場を仮定しているため、地盤反力の影響を予め積分して弾性支承上の梁をあたかもばね支点を持つ梁のように扱うことが可能であり、取扱いが非常に簡単になる。もちろん、地盤反力の影響をばね支点的に取り扱うため、地盤の非線形特性も容易に取り込むことができる。
さて、
6章で説明したように、川井モデルの梁要素と平面要素を組み合わせた解析ではその接合部において
図8.2のような平面要素のばねを考えた。これは、梁要素から見れば重心点に集中化を行った支点ばねを持ったのと同じ結果になる。そこで、この方法と同様な考え方に基づき梁要素の重心に、変位に抵抗する支点ばねを追加してみよう。このように考えると、近似的ではあるが、弾性支承上の梁と同様な解析を行うことができる。
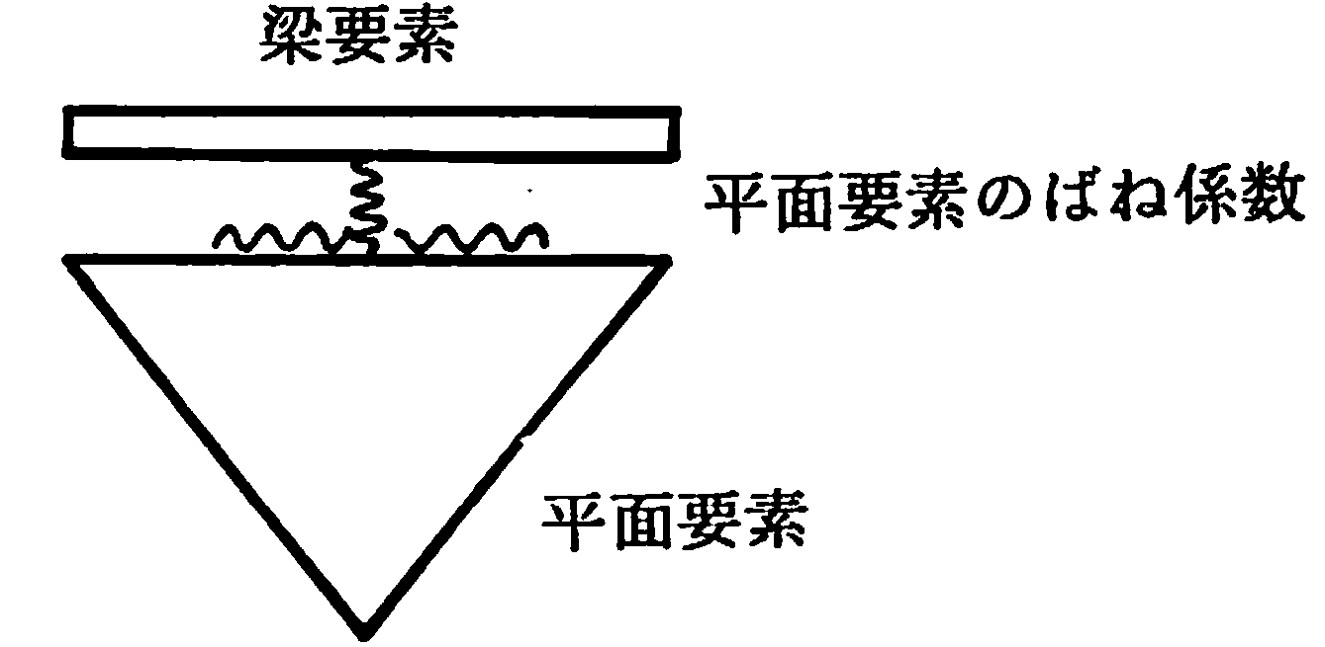
$\hspace{1em}$図8.2 梁要素と平面要素の間のばね係数
図8.3(a)は剛体変位場を仮定した一つの梁部材が弾性地盤上に置かれているという状態をモデル化したものである。$k_n、k_s$ は、それぞれ、垂直地盤反力係数と摩擦係数である。いま、要素重心の局所座標系に関する剛体変位を $(\overline{u},\overline{v},\overline{\theta})$ とすれば、各部材毎に以下のような積分を行なうことで地盤反力を求めることができる。
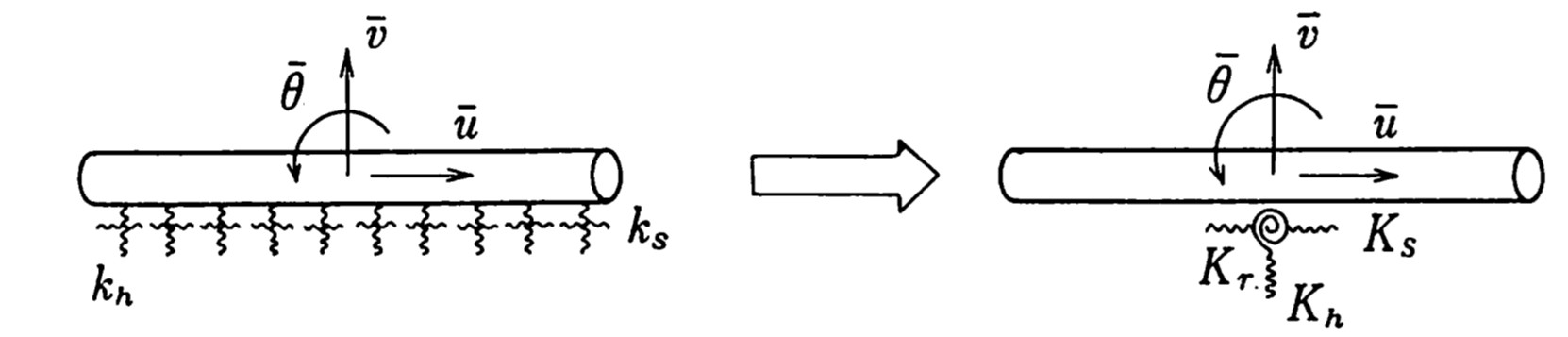
$\hspace{2em}$(a) 弾性地盤上のばね
$\hspace{6em}$(b) 積分後の地盤ばね
$\hspace{8em}$図8.3 地盤ばねの集中化
\[{\rm (8.2)}
\left\{
\begin{array}{rcl}
K_{n} \cdot \overline{v} &=& \displaystyle
\int_{-l/2}^{l/2} k_{n}(\overline{v}+
\cdot \overline{x} \cdot \overline{ \theta} ) dx
= (k_{n} l ) \; \overline{v}
\\
K_{r} \cdot \overline{\theta} &=& \displaystyle
\int_{-l/2}^{l/2} k_{n}(\overline{v}+
\cdot \overline{x} \cdot \overline{ \theta} ) \overline{x} dx
= (\frac{k_{n} l^{3}}{12} ) \; \overline{\theta}
\\
K_{s} \cdot \overline{u} &=& \displaystyle
\int_{-l/2}^{l/2} k_{s}\overline{u} dx
= (k_{s} l ) \; \overline{u}
\end{array}
\right.
\]
ここで、$K_n$、$K_s$、$K_r$ は支点ばね係数で
\[{\rm (8.3)}
K_{n} = k_{n} l \;, \;\;\;\;
K_{r} = \frac{k_{n} l^{3}}{12} \;, \;\;\;\;
K_{s} = k_{s} l
\]
であり、
図8.3(b)のように設定される。本モデルでは、回転に抵抗するばね $K_r$ があるため、地盤反力は線形分布になることが理解できる。
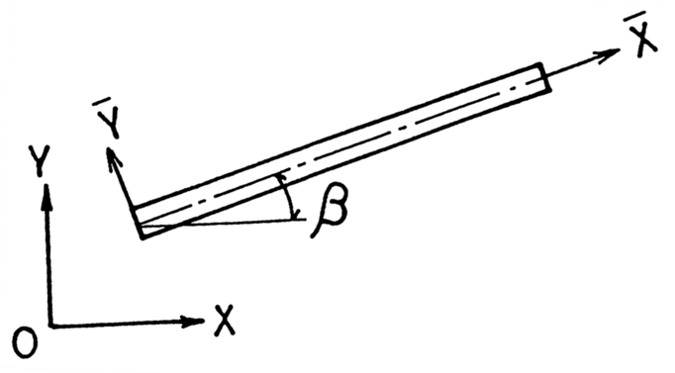
$\hspace{0em}$図8.4 部材座標系と全体座標系
マトリックスを用いてこれを整理すると以下のようになる。
\[{\rm (8.4)}
\overline{\boldsymbol{R}} = -
\left[
\begin{array}{ccc}
K_{s} & 0 & 0 \\
0 & K_{n} & 0 \\
0 & 0 & K_{r}
\end{array}
\right]
\left\{
\begin{array}{c}
\overline{u} \\
\overline{v} \\
\overline{\theta}
\end{array}
\right\}
= - \overline{\boldsymbol{k}} \cdot \overline{\boldsymbol{u}}
\]
この式は部材座標系に対して立てられた関係式であり、全体剛性行列に組み込むためには座標変換を行っておく必要がある。
図8.4のように２つの座標系を考えると、この座標変換行列は
\[{\rm (8.5)}
\boldsymbol{T} =
\left[
\begin{array}{ccc}
\;\;\; \cos \beta & \sin \beta & 0 \\
-\sin \beta & \cos \beta & 0 \\
\;\;\; 0 & 0 & 1
\end{array}
\right]
\]
となる。したがって、反力は以下のように変換される。
\[{\rm (8.6)}
\boldsymbol{R} = \boldsymbol{T}^{t} \cdot \overline{\boldsymbol{R}}
=-\boldsymbol{T}^{t} \cdot \overline{\boldsymbol{k}} \cdot
\boldsymbol{T} \cdot \boldsymbol{u}
=-\boldsymbol{k} \cdot \boldsymbol{u} \;\;\;\;\;
( \boldsymbol{k} = \boldsymbol{T}^{t} \cdot \overline{\boldsymbol{k}}
\cdot \boldsymbol{T} )
\]
一方、全体剛性行列を組み立てたときの連立方程式は、この地盤反力を考慮して以下のように与えられる。
\[{\rm (8.7)}
\boldsymbol{K} \cdot \boldsymbol{u} = \boldsymbol{P} + \boldsymbol{R}
= \boldsymbol{P} - \boldsymbol{k} \cdot \boldsymbol{u}
\]
ここで、$\boldsymbol{K}$ は全体剛性行列で、$\boldsymbol{P}$ は荷重項である。この場合、地盤反力には変位に関する未知数が含まれているため、最終的には次のような方程式を解けばよいことになる。
\[{\rm (8.8)}
(\boldsymbol{K}+ \boldsymbol{k}) \; \boldsymbol{u} = \boldsymbol{P}
\]
以上のように、要素内変位場を剛体と仮定することにより、地盤反力分布ばねの集中化が容易に行え、近似的とはいえ要素分割にあまり左右されない支点ばねを用いた弾性支承上の梁を誘導することができる。本モデルはせん断ばね $K_s$ の存在からも理解できるように、摩擦の影響も簡単に取り込むことができる。また、この梁要素はせん断変形の影響が考慮されているため、大口径の場所打ち杭や地中連続壁の解析などにも有効に利用できるものと思われる。
簡単な数値計算例により本モデルの精度を検証してみよう。解析に用いたモデルを
図8.5に、また、材料定数を
表8.1に示す。境界条件として杭先端を自由、ヒンジ、固定とした場合の３通りを考えた。また、荷重条件としては杭頭にせん断力を与えた場合とモーメントを与えた場合の２通りを考えている。
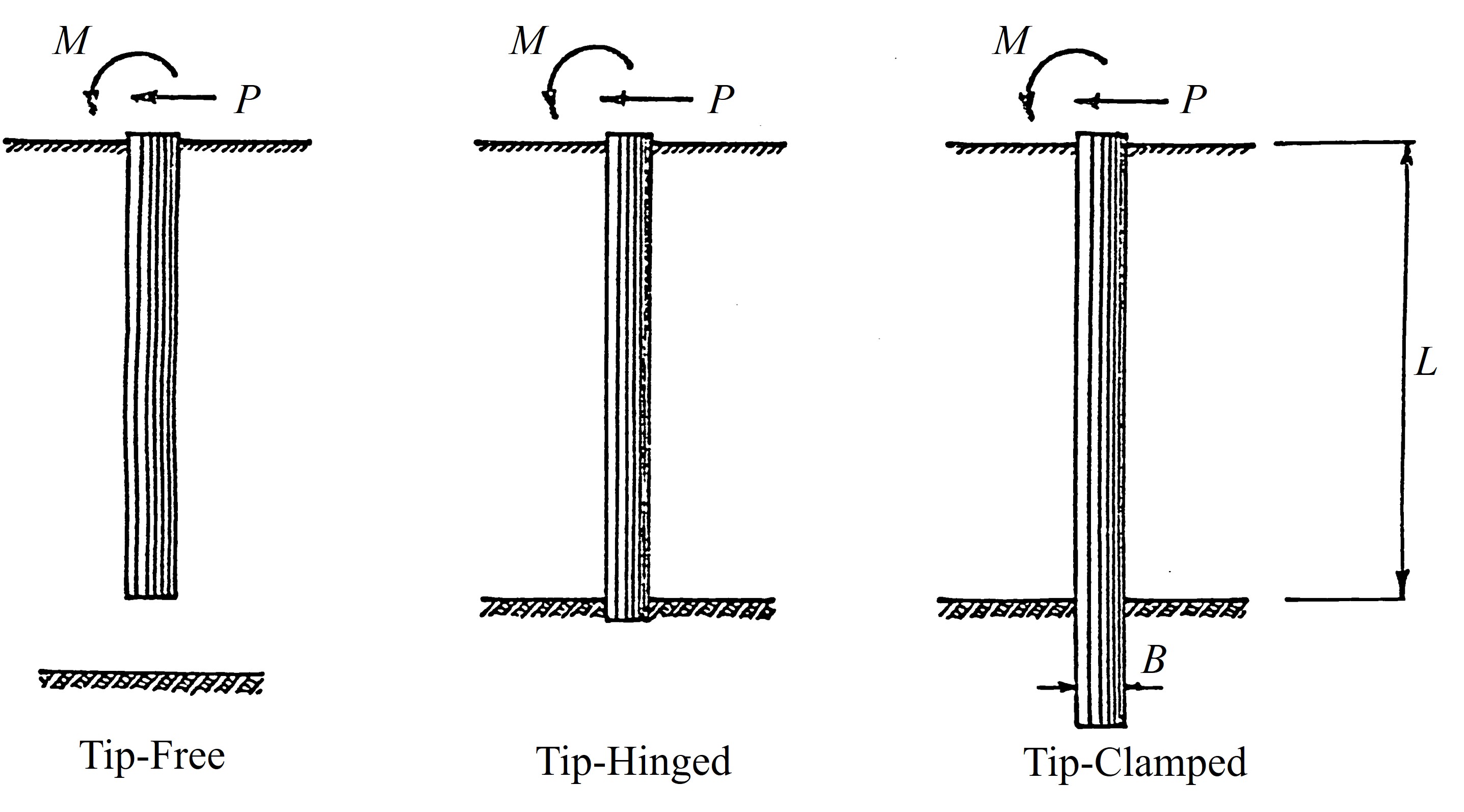$\hspace{8em}$図8.5 数値計算モデル
表8.1 材料定数と荷重値
| 材料と荷重 |
単位 |
値 |
| 弾性係数 $(E)$ |
${\rm kg/cm^2}$ |
350000 |
| 水平地盤反力係数 $(K)$ |
${\rm kg/cm^3}$ |
0.5 |
| 断面２次モーメント $(I)$ |
${\rm cm^4}$ |
103200 |
| 杭径 $(B)$ |
${\rm cm}$ |
40 |
| 杭長 $(L)$ |
${\rm cm}$ |
1000 |
| 水平力 $(P)$ |
${\rm kg}$ |
2000 |
| 曲げモーメント $(M)$ |
${\rm kg \cdot cm}$ |
300000 |
表8.2は杭頭のたわみを解析解と比較したもので、粗い分割であってもよい解が得られており、分割数が多くなるほど精度が上昇する。杭頭にせん断力を与えた場合、解析解より大きめの変位がえられているが、これは解析解においてせん断変形の影響が考慮されていないためと思われる。
表8.2 杭頭のたわみ
| 荷重 |
先端自由 |
先端ヒンジ |
先端固定 |
分割数 |
| 理 論 解 |
計算結結果 |
理 論 解 |
計算結結果 |
理 論 解 |
計算結結果 |
| P (2 t) |
0.6869 |
0.6709 |
0.6856 |
0.6756 |
0.6812 |
0.6725 |
4 |
| 0.6871 |
0.6858 |
0.6818 |
8 |
| 0.6877 |
0.6864 |
0.6821 |
16 |
| M (3 tm) |
0.3532 |
0.3087 |
0.3538 |
0.3093 |
0.3503 |
0.3065 |
4 |
| 0.3423 |
0.3429 |
0.3396 |
8 |
| 0.3505 |
0.3511 |
0.3476 |
16 |
図8.6は先端固定の状態にせん断力を作用させた場合の曲げモーメント分布とその収束性を示した図である。粗い分割の場合、$x=10 {\rm m}$ でモーメントの値が解析解と大きく異なっているが、絶対値で見ると曲げモーメントが非常に小さい位置であるため、全体に与える影響は少ない。
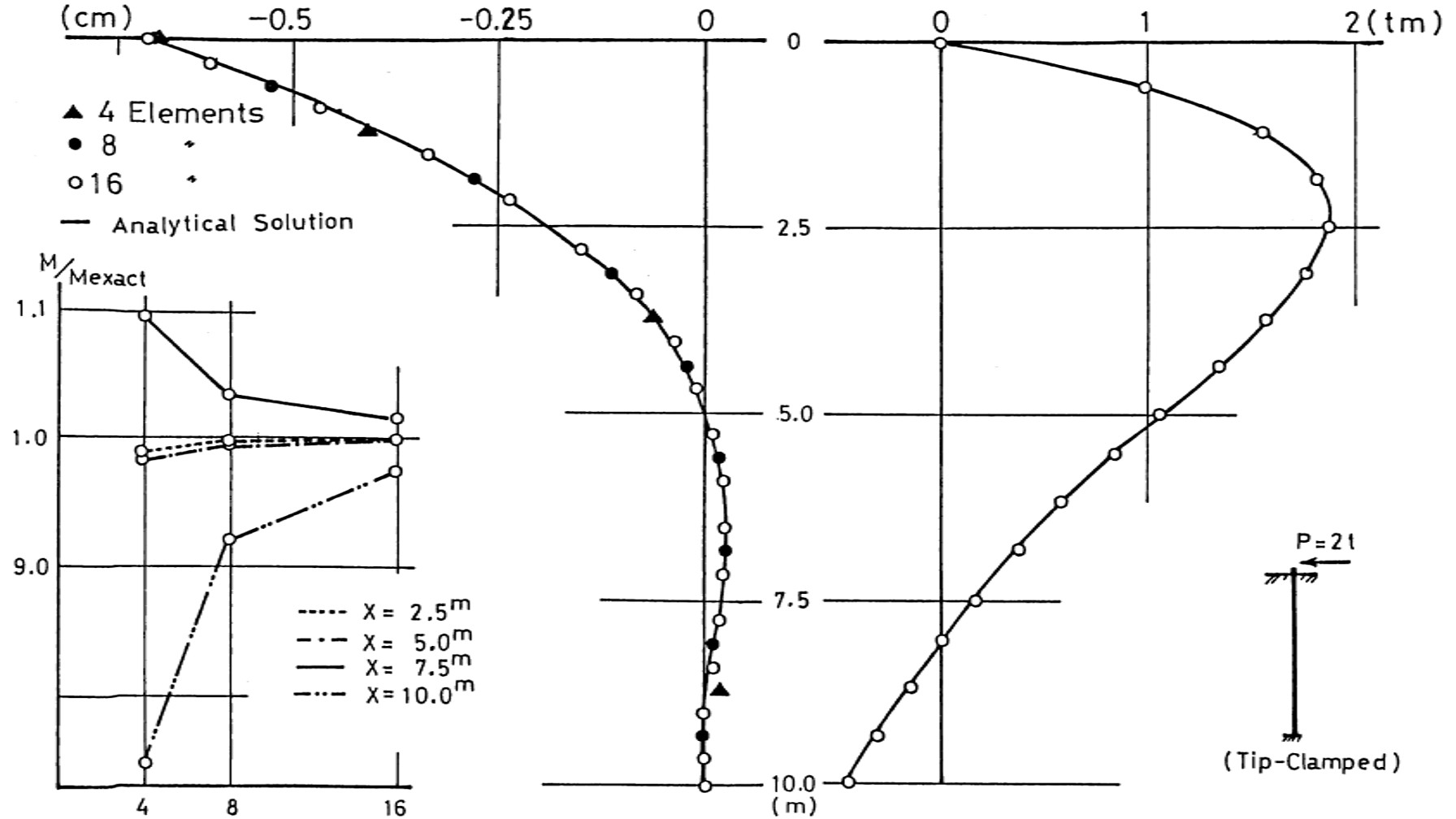
$\hspace{8em}$図8.6 先端固定，水平荷重作用の場合
同様に、曲げモーメントを作用させた場合の結果が
図8.7に示されている。せん断力を作用させた場合と同様、よい精度で解が得られていることが理解できよう。
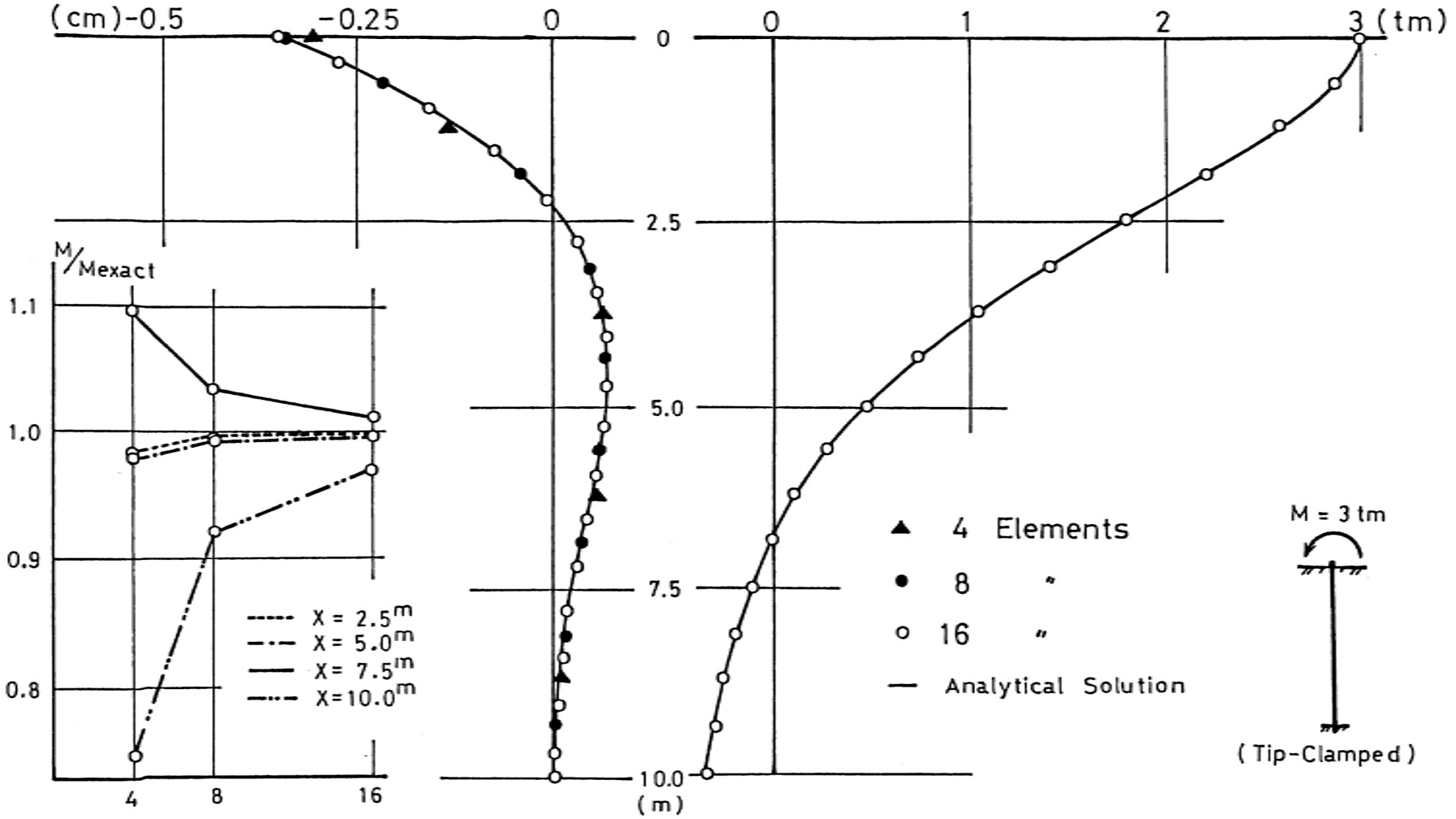
$\hspace{4em}$図8.7 先端固定，モーメント作用の場合
杭の横抵抗に関する議論は数多くなされているが、基本的には次の３つに大別される。
- （１）極限地盤反力法
- （２）弾性地盤反力法（線形・非線形弾性）
- （３）複合地盤反力法（p－y曲線法）
（１）の
極限地盤反力法は土の極限状態における地盤反力の分布を経験的あるいは実験的に仮定し、杭に作用する外力との釣合から杭の横抵抗を求める方法で、杭のたわみに直接関係しない方法である。この方法はケーソンの設計などに利用されている。
（２）の
弾性地盤反力法は地盤反力をはり理論から得られるたわみの $n$ 乗に比例するとして計算する方法であり、$n=1$ する
線形地盤反力法と $n \neq 1$ とする
非線形地盤反力法の２種類に分けることができる。前者の考え方は
8.1節で説明したとおりであり、後者の方法は若干複雑になる傾向がある。非線形地盤反力法にはいくつかあるが、
港湾方式と呼ばれる方法が著名である。
（３）の
複合地盤反力法は塑性域を考慮し、その塑性域では（１）の方法を、弾性域については（２）の方法を用いて計算しようとするものである。
本節では、土を完全弾塑性体と仮定した（３）の複合地盤反力法の立場から説明する。これは、杭本体の非線形構造解析において山田の方法による非線形解析法を採用するためであり、この方法により地盤破壊を考慮すれば地盤と杭本体の破壊を同時に、しかも簡単に取り扱うことができるためである。
全弾塑性体では、地盤反力が極限抵抗土圧強度に達するまでは地盤を線形弾性体とし、それ以降は一定としている。非線形解析法に山田の方法を用いれば、地盤が破壊するための荷重増分率と杭が破壊するための荷重増分率の２つが求められる。このうち、小さい方の値を採用して増分計算を行えば、両者の破壊を同時に考慮できることになる。
図8.8にこの計算の流れを示す。
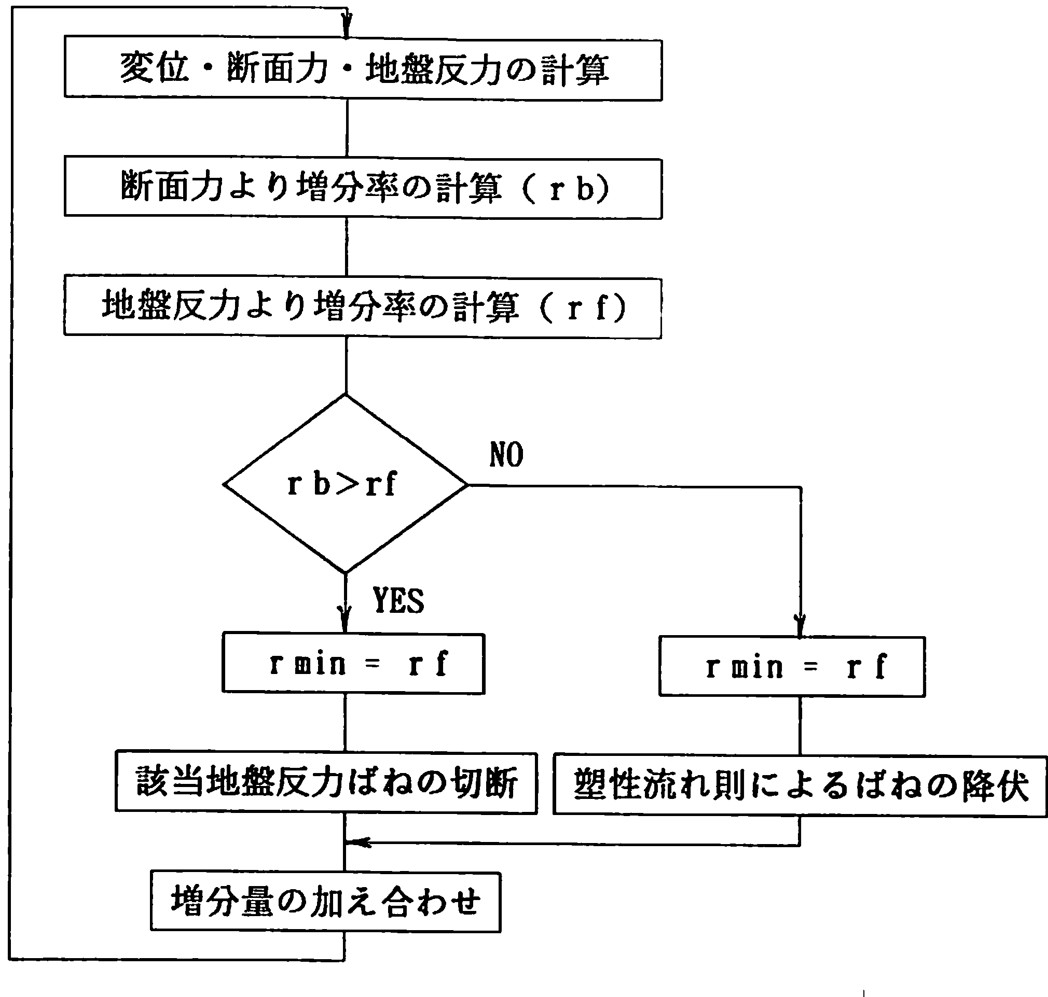
$\hspace{4em}$図8.8 弾塑性地盤上の梁の解析法
地盤を完全弾塑性と仮定した場合、この地盤が破壊するために必要となる荷重増分率 $(r_f)$ は
図8.9のように予め極限抵抗土圧強度を与えておき、以下の計算より求めることができる。
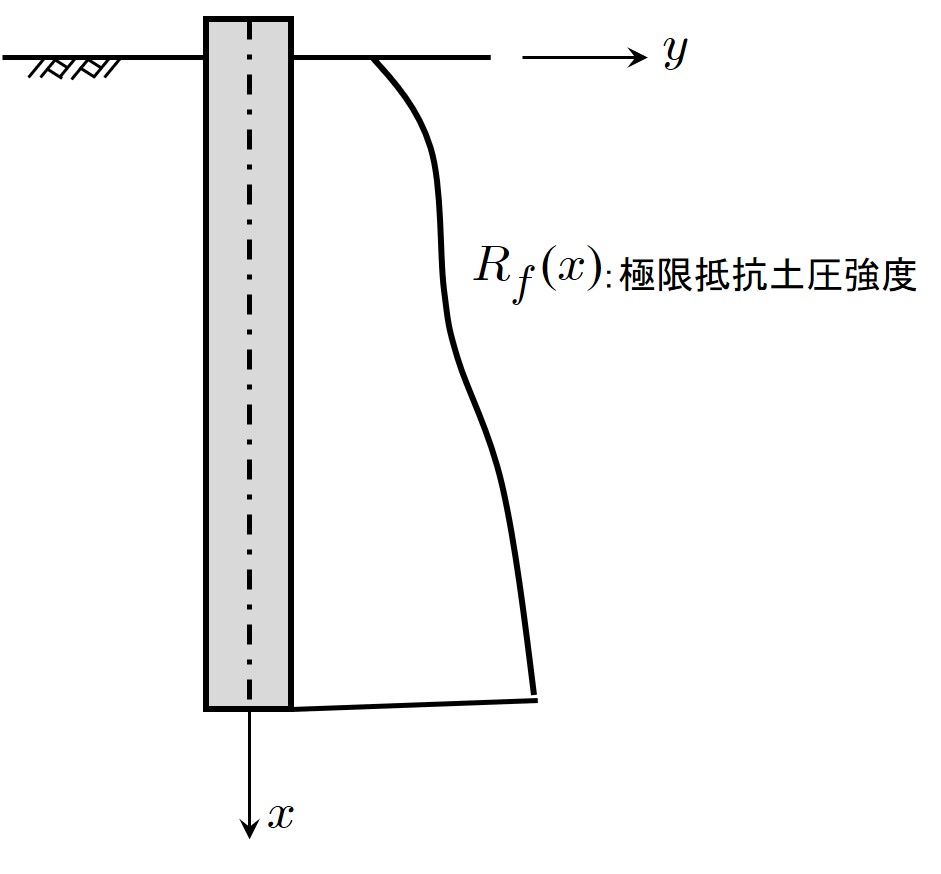
$\hspace{2em}$図8.9 極限地盤反力強度分布
\[{\rm (8.9)}
r_{f} = \frac{R_{f}(x)}{R(x)}
\]
ここで、$R$ は計算によって求められた地盤反力である。
極限抵抗土圧強度については幾つかの分布が提案されており、どの方法を用いるかは問題に応じて選択すればよい。ここでは、「建築基礎構造設計規準・同解説」に掲載されている
Bromsの方法を利用し、簡単な数値計算例から本手法の有効性を検証してみる。
軟らかい粘土の極限抵抗土圧強度 $P_u$ は地表面を除いて $8C_u～12C_u$ の間で変化すると言われている。本書では地表面付近の破壊を考慮し、
図8.10に示すよう深さ方向に強度を変える。図中の $X_R$ は以下のように仮定する。
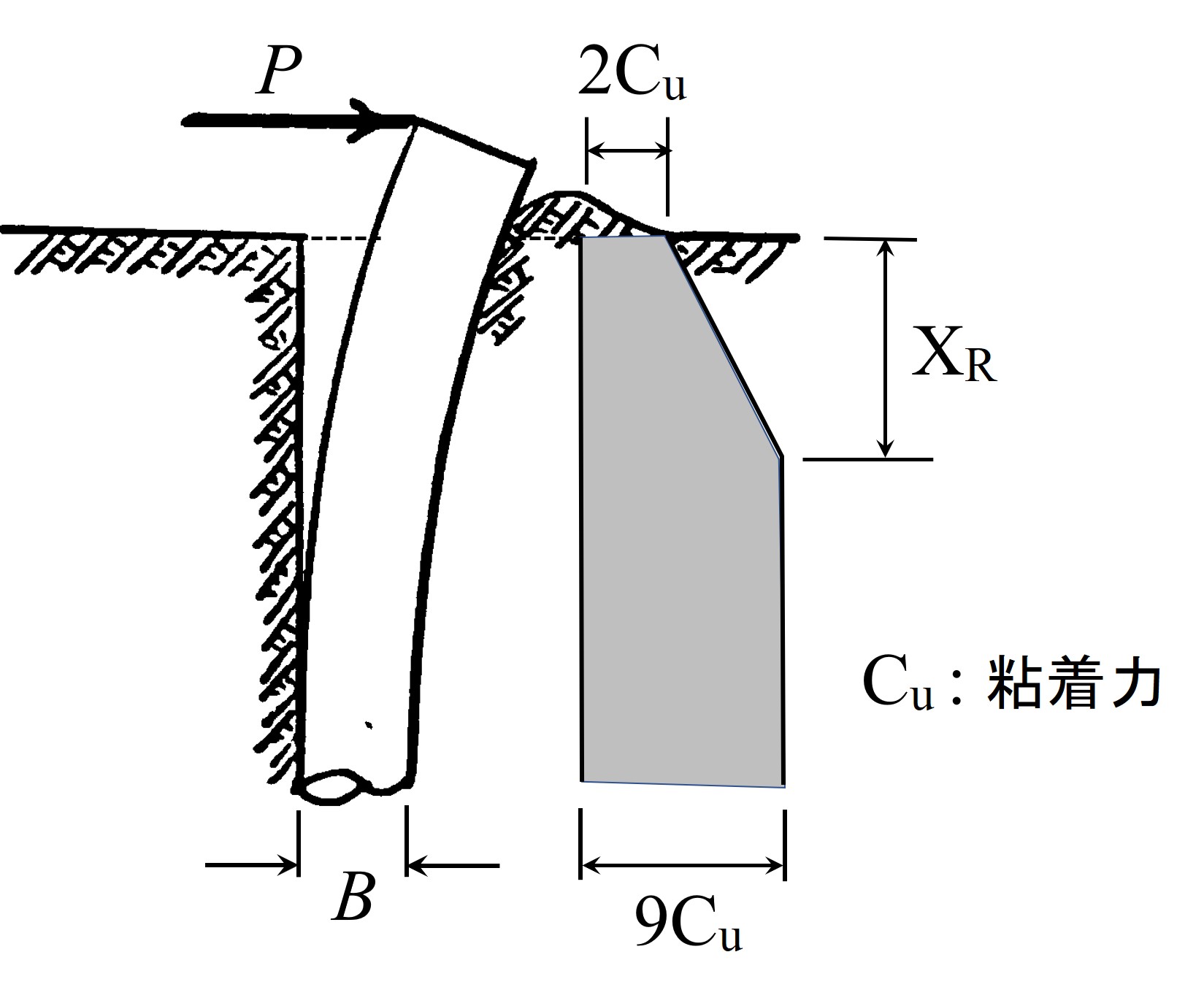
$\hspace{0em}$図8.10 粘性土の地盤反力分布
\[{\rm (8.10)}
X_{R} = \frac{6B}{\displaystyle \frac{ \gamma B}{C_{u}} + J }
\]
ここで、$B$ は杭径または杭幅、$\gamma$ は土の有効単位体積重量、$J$ は定数で、やや硬い粘土の場合0.25、軟らかい粘土の場合0.5である。
弾塑性地盤上の梁に対する極限水平抵抗を検討するため、
図8.11に示すような簡単なモデルを設定し、水平荷重を与えて解析した。杭は肉厚 $t$ の中空鋼管杭とし、杭長は3mを最も短い杭として1.5m づつ増加させ７ケース計算した。また、杭本体の要素分割長は0.5mとしている。
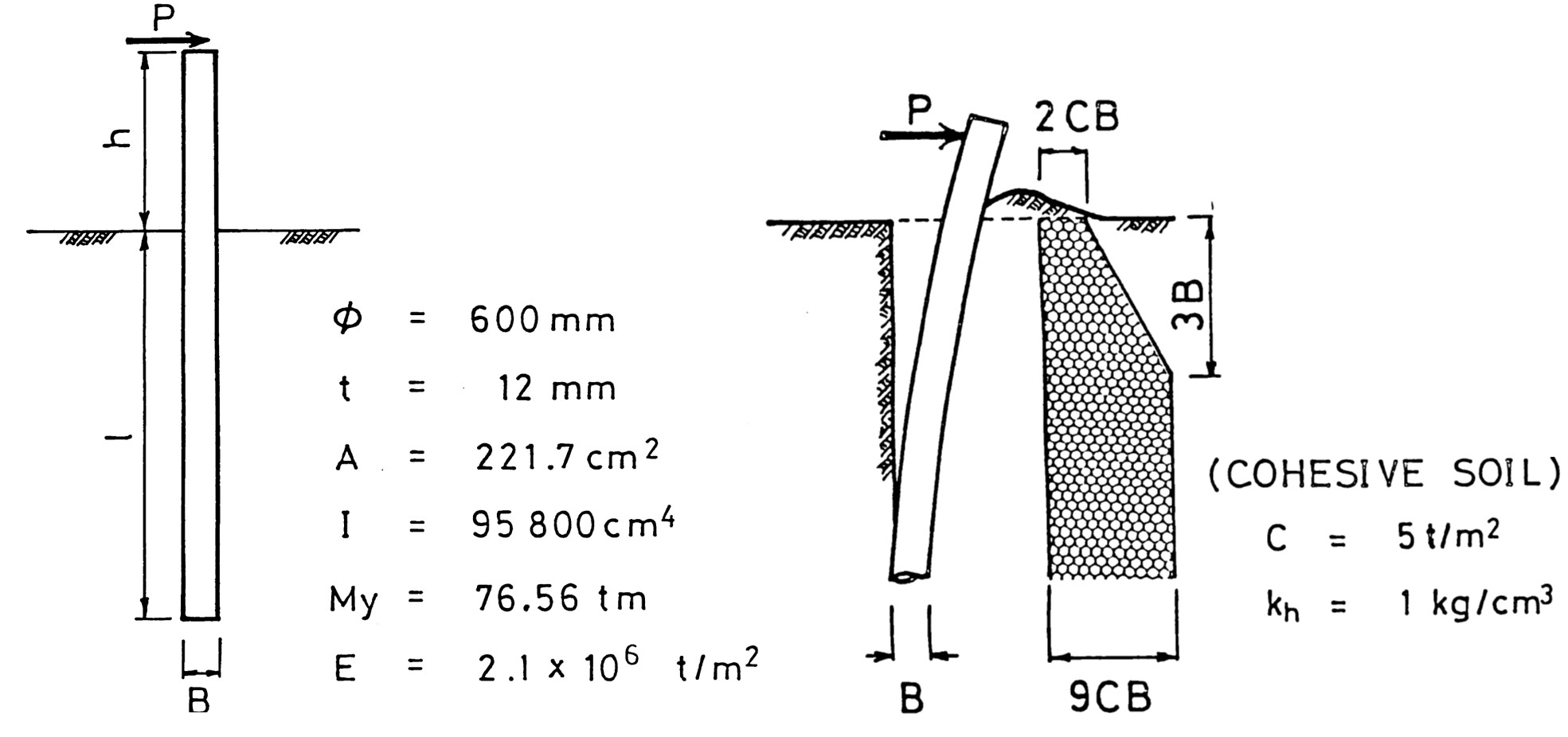
$\hspace{3em}$(a) 杭
$\hspace{14em}$(b) 地盤
$\hspace{7em}$図8.11 解析に用いたモデル
図8.12は地盤反力分布を、また、
図8.13は杭の変形を示した図である。短い杭では、地盤の破壊により転倒する傾向があるが、杭長が長くなるにつれ、その傾向は無くなってくる。
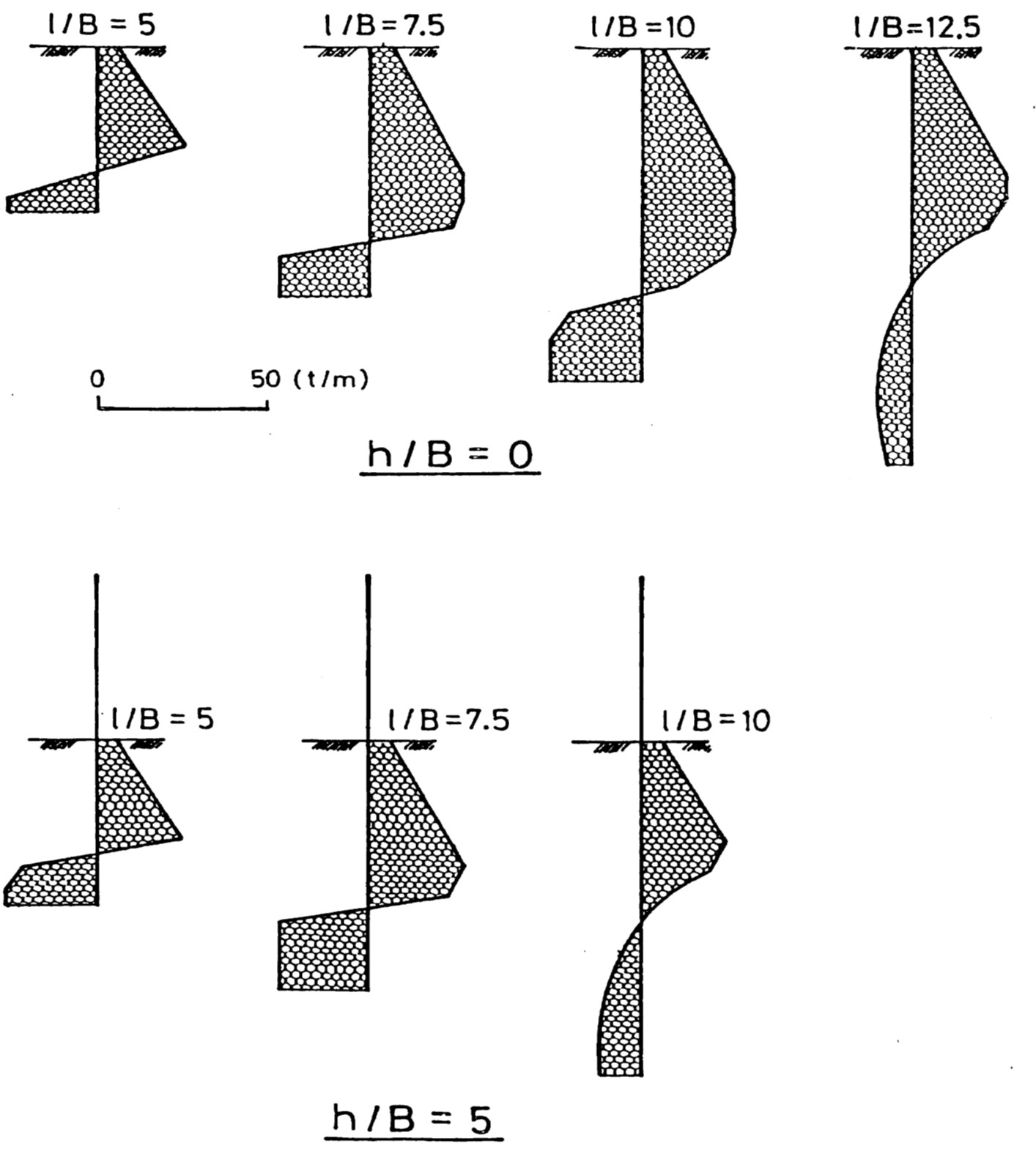
$\hspace{2em}$図8.12 地盤反力分布
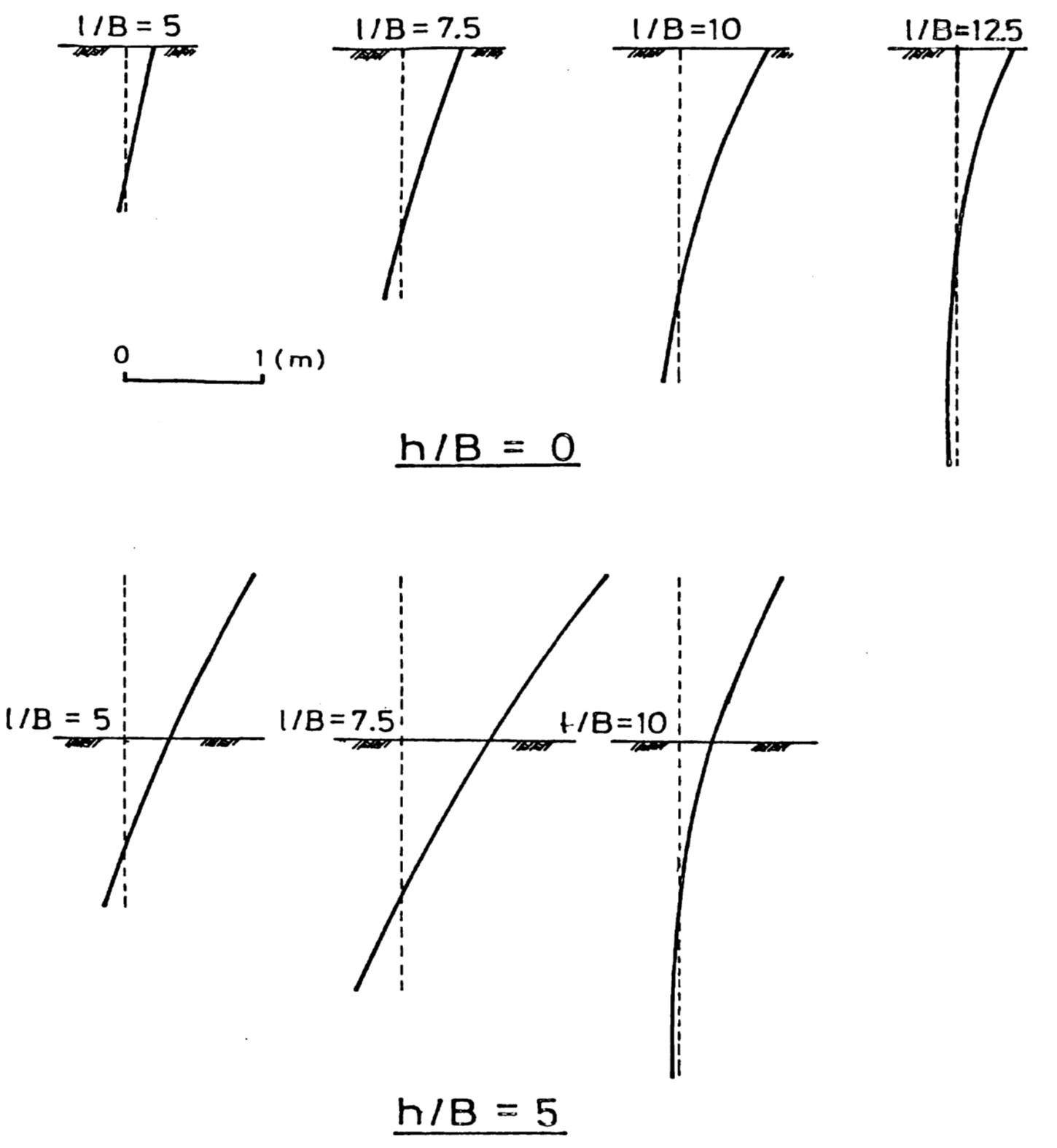
$\hspace{2em}$図8.13 杭のたわみ
図8.14は地盤と杭の破壊状況を示した図であり、この図より根入れの浅い短い杭では地盤の破壊のみで崩壊荷重が決定し、根入れ比 $(l/B)$ が10以上になると杭本体に塑性ヒンジが発生し極限水平抵抗が決定する結果となっている。この後、杭長を長くしても極限水平抵抗は変化しない。図下段は杭頭部が突出している場合の結果でやはり同様な結果となっている。
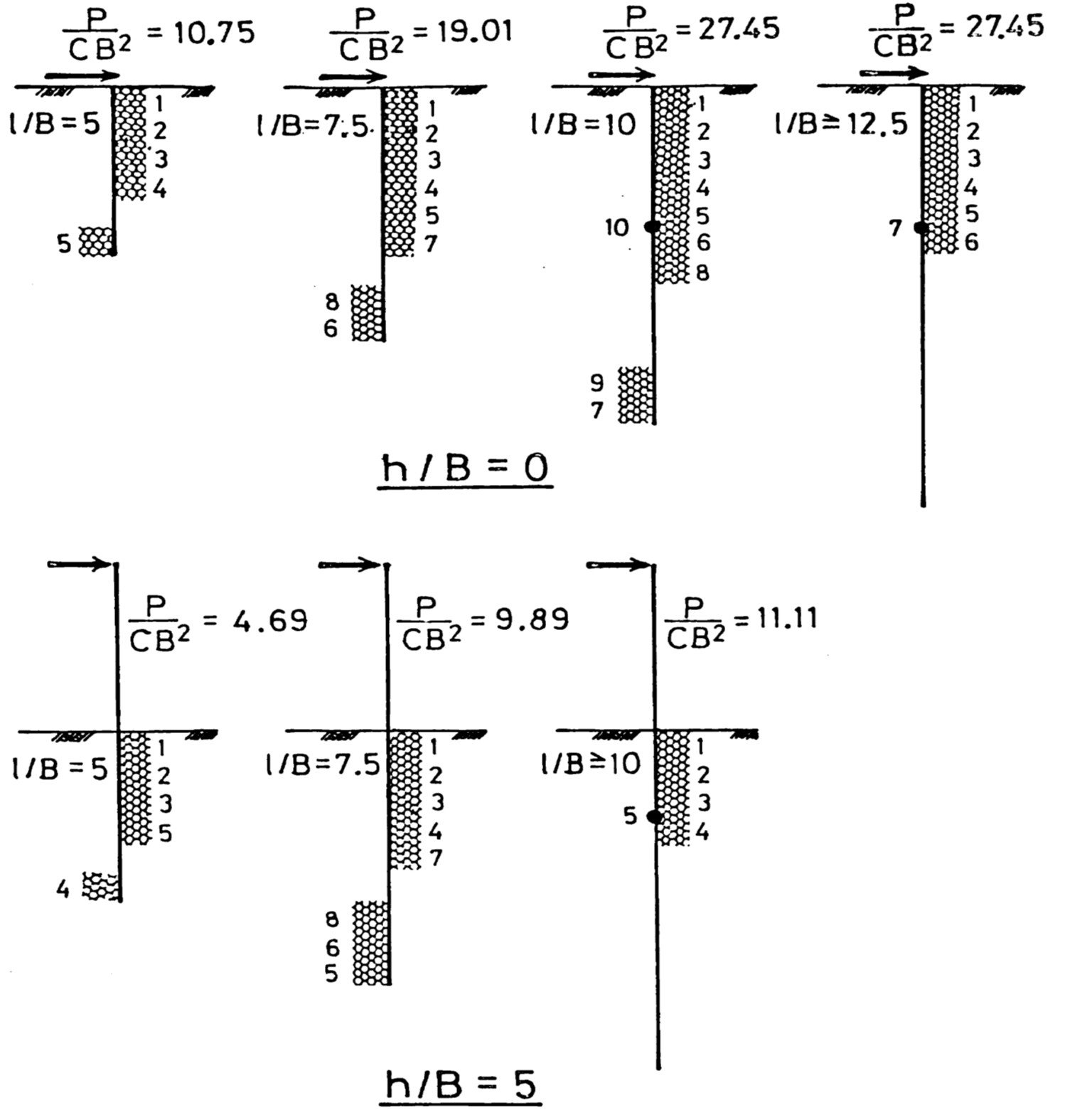
$\hspace{2em}$図8.14 地盤と杭の破壊状況
図8.15は粘性土に対する本手法の極限荷重とBromsの解を比較した結果である。図中、実線がBromsによる短い杭、点線が長い杭の極限荷重である。このように、Broms による場合、短い杭と長い杭について場合分けを行わなければならないのは、杭本体に塑性ヒンジが発生して破壊に至る場合と地盤の破壊だけで極限荷重が決まる場合の２通りが考えられるからである。しかし、本手法では増分計算を行うことで地盤と杭本体の破壊を同時に扱うことができるため、そのような場合分けを意識する必要はない。両者の結果を比較すると、短い杭、長い杭の相違が離散化極限解析解において評価できることが理解できよう。
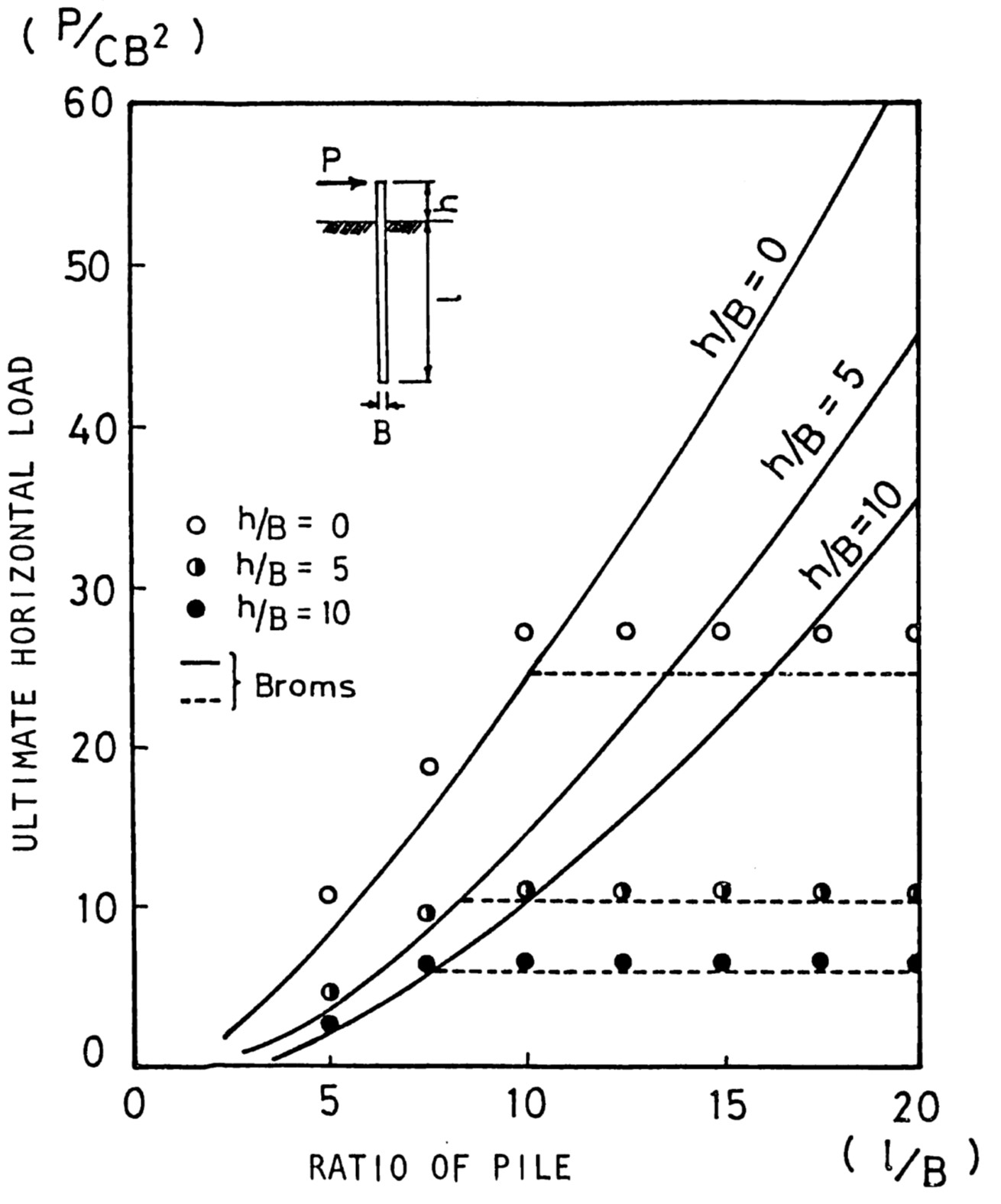
$\hspace{2em}$図8.15 極限水平抵抗の簡易解との比較
さて、モデルの誘導においても説明したように、地盤を考慮した川井モデルによる梁要素には摩擦の影響を考慮できるせん断方向のばねが含まれている。もちろん、杭の各部において摩擦係数は同一である必要はなく、摩擦に関する非線形性を容易に考慮することができる。非線形解析のアルゴリズムについては基本的に極限水平抵抗の場合と同様であり、山田の方法により摩擦に関する荷重増分率を計算し、他の荷重増分率と同時に考慮すればよい。次に、このような摩擦の影響を取り入れた解析例を示そう。
図8.16は長さ30mの杭が支持層に十分根入れされた場合のモデルで、荷重は鉛直方向からのみ作用している。モデル化にあたり、支持層については鉛直方向のみをばね支点として取り扱っている。計算に用いた材料定数は図に示す通りである。ただし、支持層は降伏しないものとする。
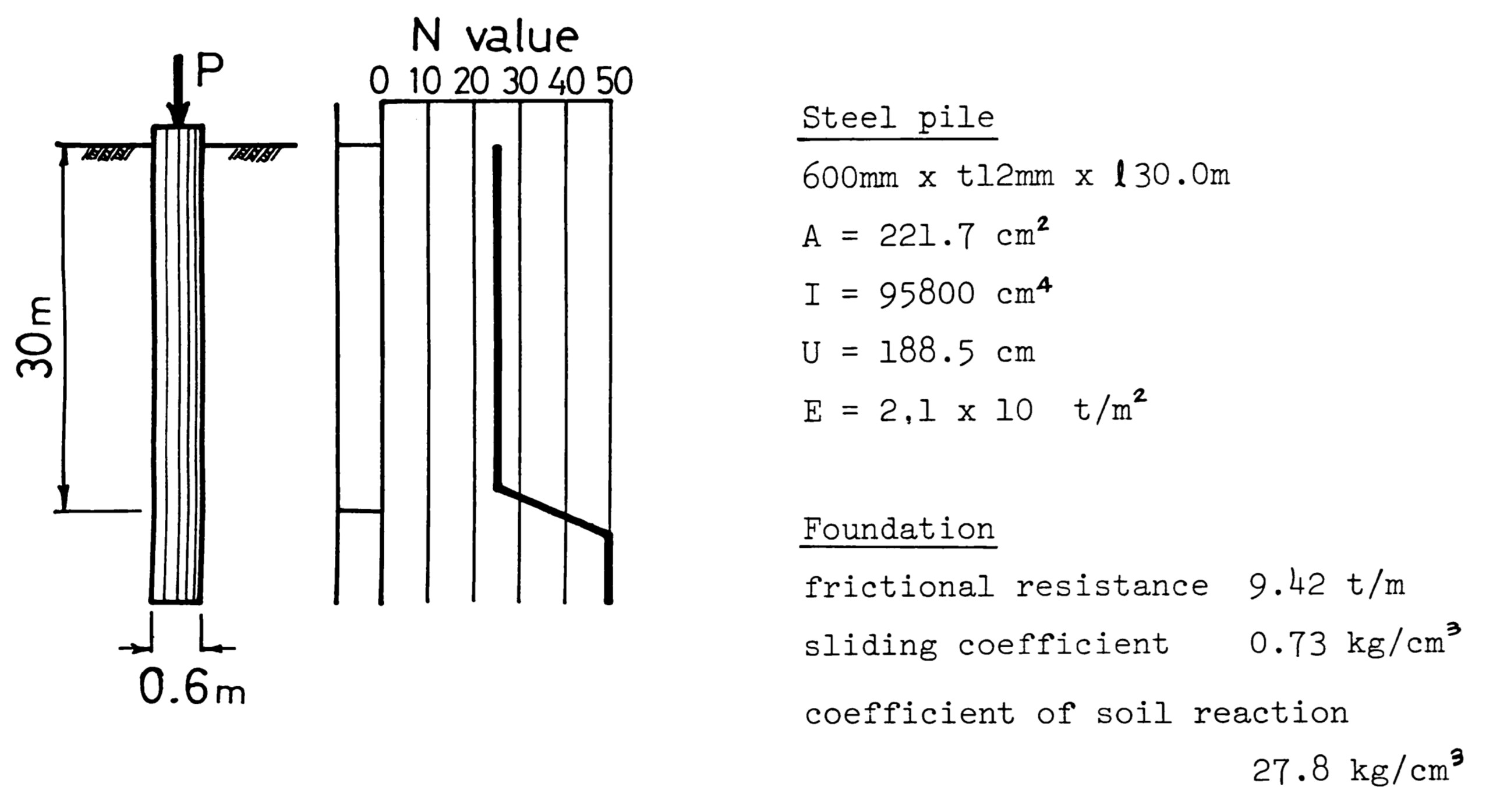
$\hspace{8em}$図8.16 摩擦杭のモデルと材料定数
図8.17は鉛直荷重と変位の関係を示した図である。P=170.9t以上の荷重が作用すると杭と地盤の間に摩擦破壊が発生する。これより小さな荷重では簡便法による変位解と4%程度の差であるが、一旦、破壊が発生するとこの差は広がり、最終的に杭周辺がすべてすべった状態では46%の差となる。しかも、このときの支持力は極限支持力よりはるかに安全側の値である。
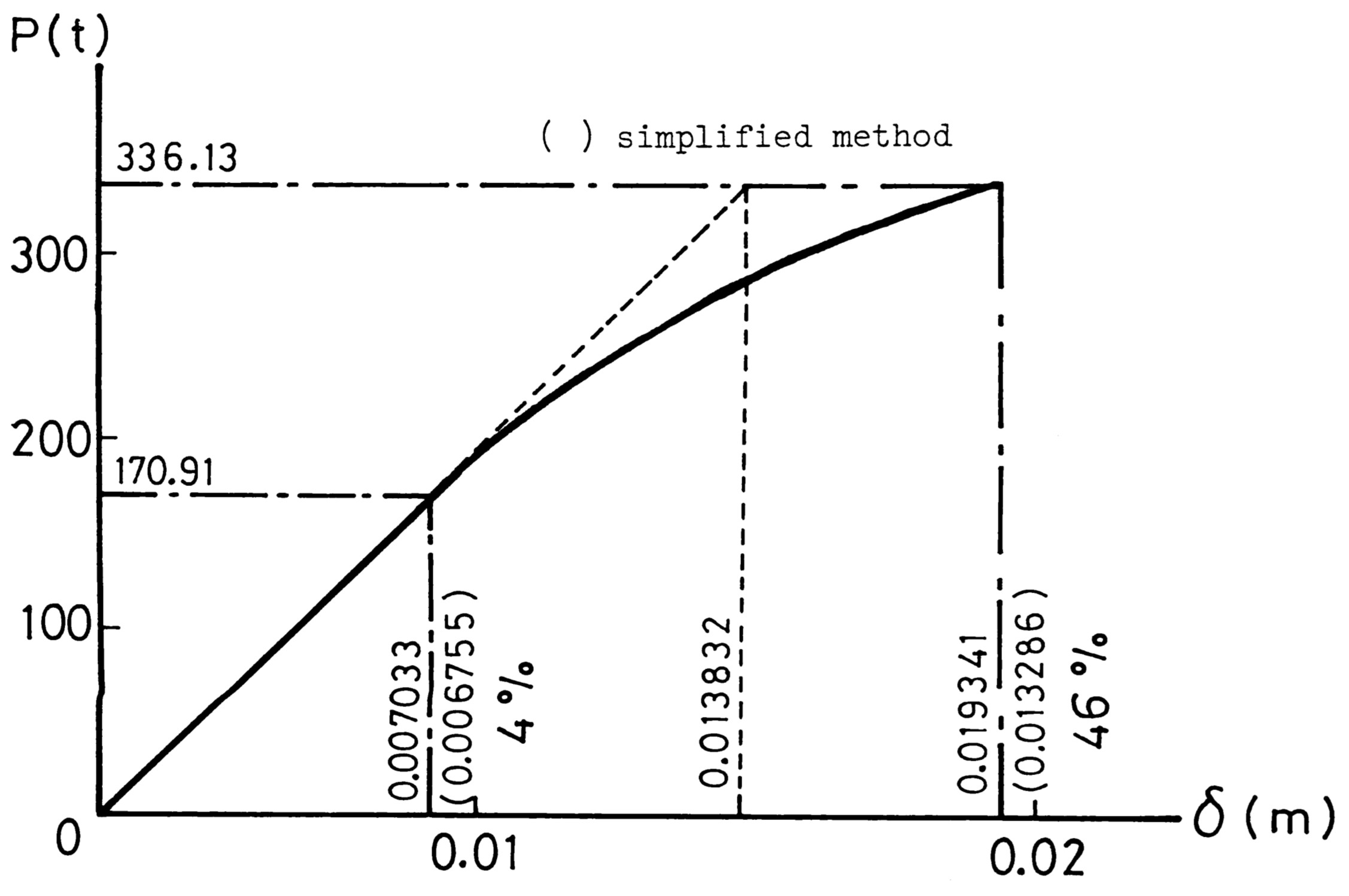
$\hspace{4em}$図8.17 摩擦杭の荷重－変位曲線
ここでは、解析を単純にするため、水平方向との組み合わせを考慮しなかったが、水平および鉛直方向の荷重が同時に作用するような場合、モール・クーロン型の破壊条件を用いて崩壊荷重を評価することも容易である。
これまでの議論はすべてひずみの時間微分、すなわち、ひずみ速度に関する項が含まれ
ていない場合についての説明であった。しかし、土は負荷速度の影響などが顕著に現れる材料
であり、そのことについ検討しておくことは重要なことである。そこで、ここでは、ひずみ
速度が応力に依存するような粘弾性挙動を示す地盤上の梁の解析法について考えてみよう。
いま、
図8.18(a)に示すよう、弾性挙動を示す記号をばねで、また、粘性挙動 を示す記号を
図(b)のようにダッシュポットで表すものとする。これらの性質は力を $P$、ばね定数を $k$、粘性係数を $\eta$ とし、たわみを $y$ とすれば、以下のような関係にある。
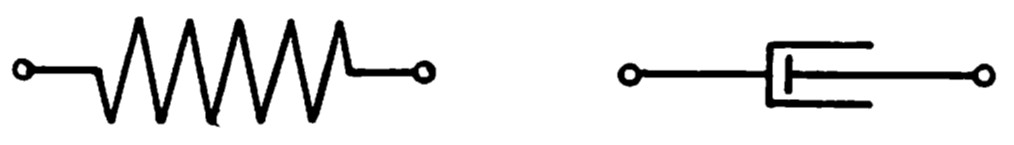
$\hspace{3em}$(a) ばね
$\hspace{5em}$(b) ダッシュポット
$\hspace{4em}$図8.18 ばねとダッシュポット
\[{\rm (8.11)}
\left.
\begin{array}{lcl}
（ばね）&P& = k \cdot y \; \\[0.5em]
（ダッシュポット）&P& = \eta \cdot \dot{y} \;
\end{array}
\right\}
\]
ここで、上付きの・は時間による変化率を表している。粘弾性体の挙動はこのばねとダッシュポットを組み合わせて表現することができ、数多くのモデルが発表されている。この種のモデルを構築する場合、数多くの実験に頼らざるをえないが現状であるため、ここでは代表的な３つのモデルを取り上げて議論することにする。
図8.19にその３種のモデルが示されている。図中の $k、k_1、k_2$ はばね定数、$\eta$ は粘性係数、$P$ は力を表すものとする。
図(a)はばねとダッシュポットが並列に結合されている
Kelvinモデルである。このモデルでは、全体の力 $P$ はばねとダッシュポットに配分されるが、たわみ $y$ が共通であるため、以下のような関係が得られる。
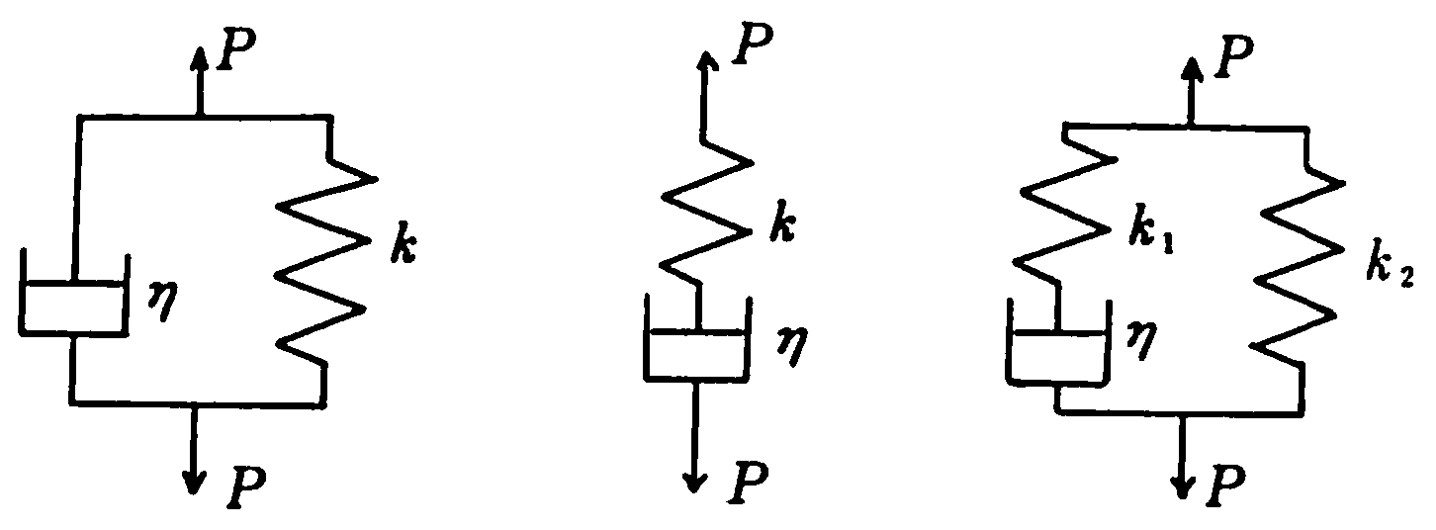
$\hspace{0em}$(a) Kelvinモデル
$\hspace{1em}$(b) Maxwellモデル
$\hspace{1em}$(c) Standard Solidモデル
$\hspace{8em}$図8.19 粘弾性モデル
\[{\rm (8.12)}
P = k \cdot y + \eta \cdot \dot{y}
\]
これを変形すれば
\[{\rm (8.13)}
\dot{y} = \frac{P}{ \eta } - \frac{y}{ \tau }
\]
となる。ここで、$\tau=\eta/k$ は
遅延時間を意味している。
図(b)はばねとダッシュポットが直列に結合されている
Maxwellモデルで、この場合、それぞれのひずみの合計が全ひずみとなるため
\[{\rm (8.14)}
\dot{y} = \frac{ \dot{P} }{ k } + \frac{P}{ \eta }
\]
となる。これを変形し
\[{\rm (8.15)}
\dot{P} = k \cdot \dot{y} - \frac{ P }{ \tau }
\]
が得られる。ここで、$\tau=\eta/k$ は
緩和時間を表している。
図(c)はばねと Maxwellが並列に結合されている
Standard Solidモデルである。図からも理解できるように
図(c)のStandard solidモデルは、
図(a)に示されるKelvinモデルと
図(b)の Maxwellモデルを重ね合わせたモデルであると考えられる。例えば、
図(c)の $k_1$ が非常に大きければKelvinモデル、$k_2$ が非常に小さければ Maxwellモデルと同じになる。これを、式により表すと以下のようになる。
\[{\rm (8.16)}
\dot{P} = (k_{1}+k_{2}) \cdot \dot{y} - \frac{ P_{1} }{ \tau }
\]
各モデルの力学特性を明確にするため、一定の力が作用した場合の時間とたわみの関係を
図8.20に示す。図より理解できるように、Kelvinモデルは、たわみ速度が時間とともに減少してゆき、最終的なたわみは Winklerの値に収束する。それに対し、Maxwellモデルでは、力が作用した瞬間は弾性たわみを示すが、その後は時間に比例してたわみが線形的に増加し、定常クリープ現象が現れる。一方、Standard solidモデルは、力が作用した瞬間では弾性挙動を示すが、その後、たわみ速度が時間とともに減少してゆき、Kelvinモデルと同様、ある一定値にたわみが収束する。３つのモデルの中では、このモデルが地盤の挙動を最も的確に現しているものと思われる。
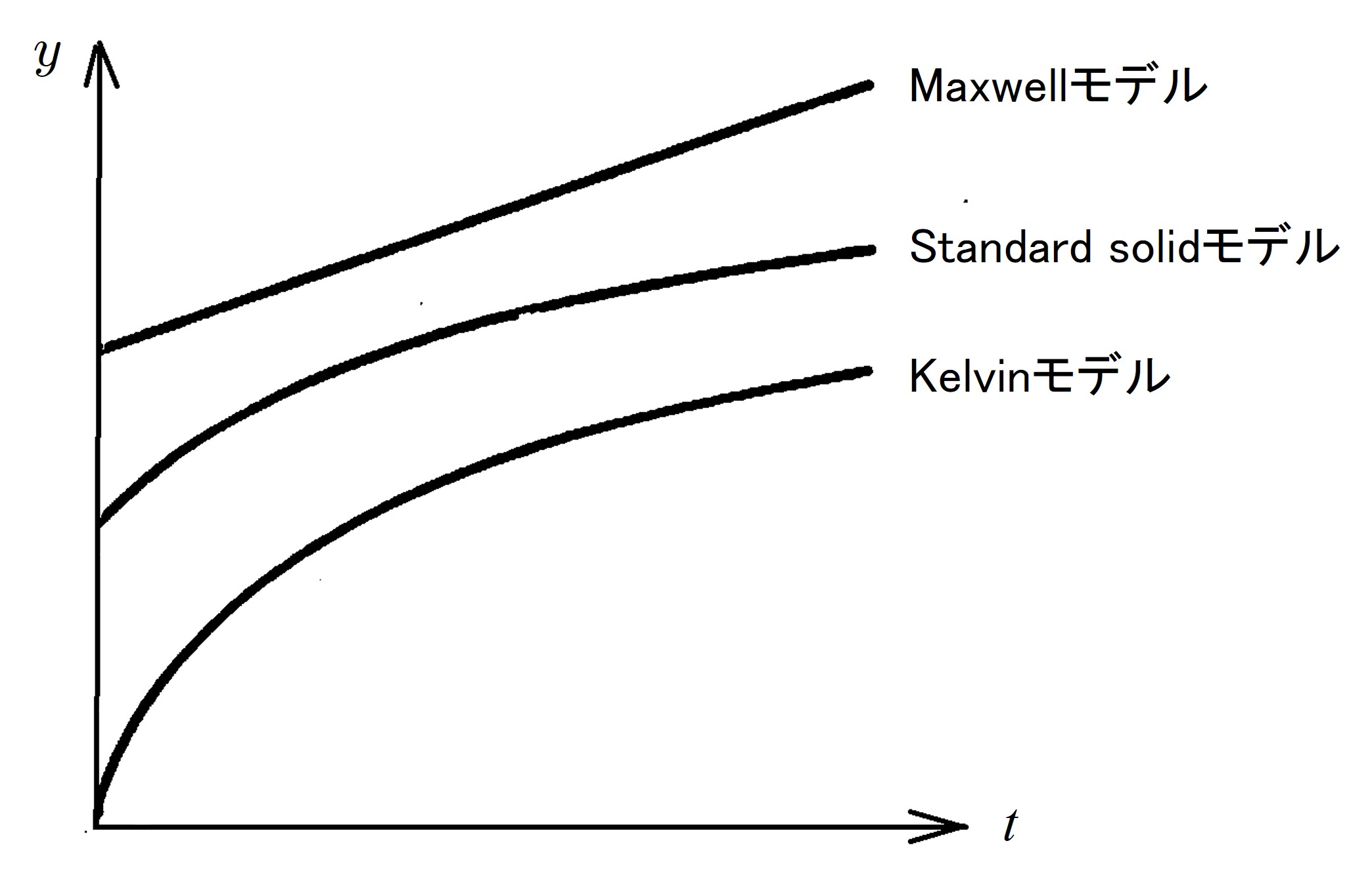
$\hspace{0em}$図8.20 一定の力が作用したときの時間・たわみ関係
このような理論式を数値計算に適した形式とするため、増分形式により表現してみよう。いま、増分力を $\Delta P$、増分変位を $\Delta y$ とすると、それぞれのモデルは以下のように増分形式で表すことができる。
- １）Kelvinモデル
\[{\rm (8.17)}
\Delta P = \frac{ \Delta y - \Delta y_{a} }{ C(t) }
\]
\[\hspace{7em}
C(t) = \frac
{1 - \left\{
1 - \exp \left( \displaystyle
- \frac{ \Delta t}{ \tau } \right)
\right\} \cdot \displaystyle \frac{ \tau }{ \Delta t }}
{ k }
\]
\[\hspace{7em}
\Delta y_{a} = \left( \frac{P}{k} - y \right)
\left\{
1- \exp \left( - \frac{ \Delta t }{ \tau } \right)
\right\}
\]
ここで、$t$ は任意の時間であり、$\Delta t$ は増分時間をを表している。
- ２）Maxwellモデル
\[{\rm (8.18)}
\Delta P = k \cdot \Delta y - P \cdot \frac{ \Delta t }{ \tau }
\]
- ３）Standard solidモデル
\[{\rm (8.19)}
\Delta P = (k_{1} + k_{2} ) \cdot \Delta y - P_{1} \cdot
\frac{ \Delta t }{ \tau }
\]
ここで、$\tau=\eta/k_1$ である。
以上の準備のもと、粘弾性地盤上の梁の定式化を行ってみよう。基本的には、３つのモデルとも同じ手順であるため、ここでは、最も地盤の特性を表現していると考えられるStandard solidモデルについて行う。
剛体変位場を仮定した川井モデルの梁要素では、梁のたわみを以下のように定義する。
\[{\rm (8.20)}
y = \boldsymbol{B} \cdot \boldsymbol{u}
\]
\[\hspace{6em}
\boldsymbol{B} = ( 1 \;, \;\; x ) \;, \;\; \boldsymbol{u}^{t} = ( v \;, \;\; \theta )
\]
いま、要素重心に作用する増分外力を $\Delta \boldsymbol{F} = \{ \Delta Y, \Delta M \}$ とすれば、地盤反力増分 $\boldsymbol{P}$ との間に以下の増分仮想仕事式が得られる。
\[{\rm (8.21)}
\Delta \boldsymbol{u}^* \cdot \Delta \boldsymbol{F}
= \displaystyle \int ( \Delta y^* \cdot \Delta P ) dx
\]
\[\hspace{9.5em}
= \displaystyle \int \Delta y^*
\left\{
\displaystyle (k_1+k_2) \Delta y - P_1 \frac{\Delta t}{\tau}
\right\} dx
\]
\[\hspace{9.5em}
= \Delta \boldsymbol{u}^* \displaystyle \int
\boldsymbol{B}^t ( k_1+k_2 ) \boldsymbol{B} dx \Delta \boldsymbol{u}
- \Delta \boldsymbol{u}^* \int \boldsymbol{B}^t \cdot
P_1 \displaystyle \frac{ \Delta t}{\tau} dx
\]
ここで、$\boldsymbol{u}^*$ は仮想増分変位を表している。これより、
\[{\rm (8.22)}
\Delta {\bf F}
= \int \boldsymbol{B}^{t} ( k_{1}+k_{2} ) \boldsymbol{B} dx \Delta \boldsymbol{u}
- \int \boldsymbol{B}^{t} \cdot P_{1} \frac{ \Delta t}{ \tau } dx
\]
なる関係が得られる。ここで、
\[{\rm (8.23)}
\int \boldsymbol{B}^{t} ( k_{1}+k_{2} ) \boldsymbol{B} dx = ( k_{1}+k_{2} )
\left[
\begin{array}{cc}
l & 0 \\
0 & \displaystyle \frac{l^{3}}{12}
\end{array}
\right] = \boldsymbol{k}
\]
\[{\rm (8.24)}
\int \boldsymbol{B}^{t} \cdot P_{1} \frac{ \Delta t}{ \tau } dx
= P_{1} \frac{ \Delta t}{ \tau }
\left \{
\begin{array}{c}
l \\
0
\end{array} \right \} = \Delta \boldsymbol{P}
\]
なる関係がある。
式(8.22)の第１項には変位に関する未知数が含まれているため、弾性地盤上の梁と同様、梁自身の剛性行列にこの関係を考慮する。
以上により、粘弾性地盤上の梁に関する定式化を行うことができた。これをもとに初期ひずみ法を適用し、非線形計算を行う。以下にその流れを簡単に示そう。
- １）時刻 $t=0$ における弾性解析を行い、その結果を初期値とする。
- ２）(1)の初期値を用い、式(8.24)より増分荷重を求める。
- ３）(2)で求まった増分荷重を作用させ、平衡方程式を解き、増分変位を求める。
- ４）式(8.19)より増分反力を計算し、増分値を初期値に加え合わせ $\Delta t$
時間後の値とする。
- ５）(4)で求まった値を新たな初期値として(2)へ戻る。
上記の手順を繰り返すことにより、任意の時刻における値を計算することができる。この計算の手順は他のモデルについても同様である。
次に本モデルにより得られる解の精度を検証するため、両端自由な一様断面を持つ梁の中央に集中荷重が作用した場合を想定し解析してみよう。材料定数は $(EI/k)/l^4=10^{-3}$ となるよう、それぞれの値を設定した。ここで、$E$ は梁の弾性係数、$I$ は断面二次モーメントである。計算に用いた増分時間は、Kelvinモデルの場合、$\Delta t/\tau=0.005$、MaxwellモデルおよびStandard solidモデルの場合、$\Delta t/\tau=0.5$としている。
図8.21、図8.22、図8.23は $\Delta t/\tau=0$ から∞までの各モデルにおけるたわみ、地盤反力、曲げモーメントを園田らの解と比較した結果である。図は要素分割数10の場合で、実線が園田らの解、〇印が本モデルによる計算結果を表している。たわみは、中央点でやや大きめの値を示しているが、全体的に眺めれば、良好な精度で解が求まっていることがわかる。
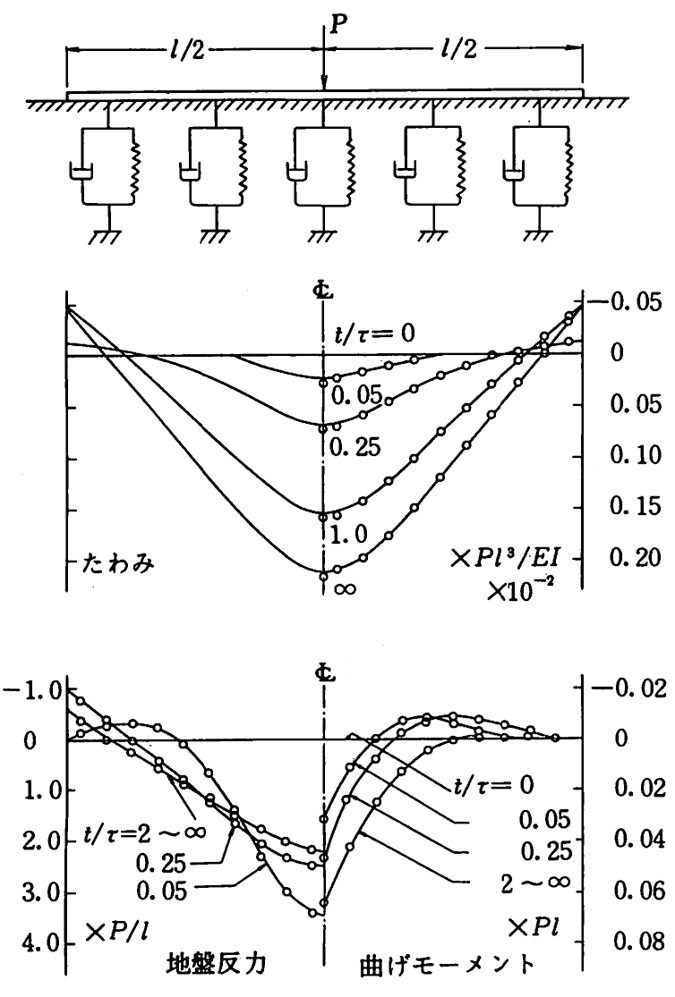
$\hspace{1em}$図8.21 Kelvinモデルの解析結果
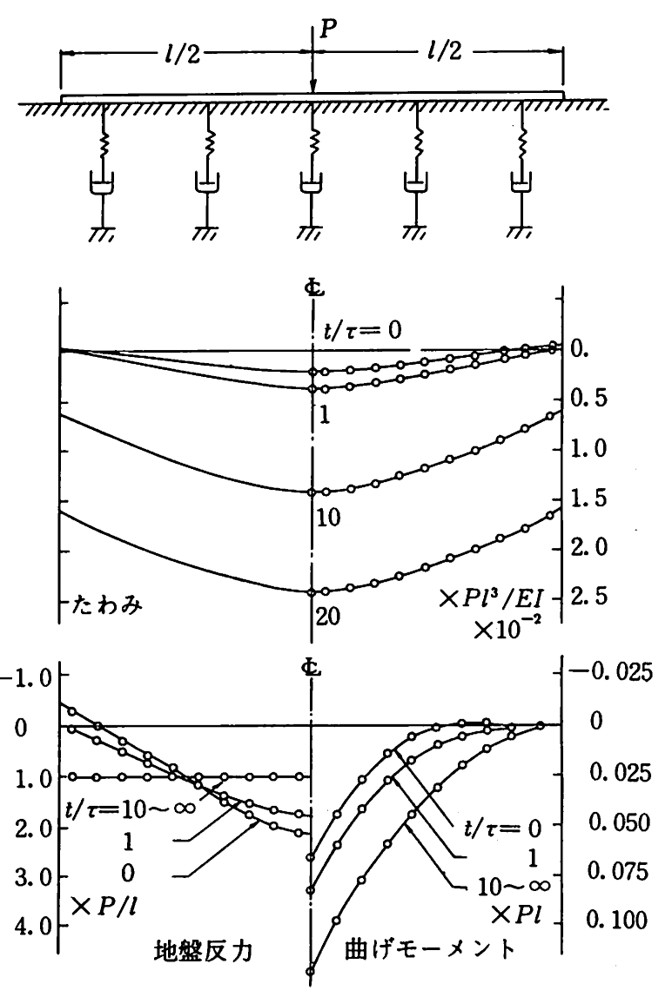
$\hspace{1em}$図8.22 Maxwellモデルの解析結果
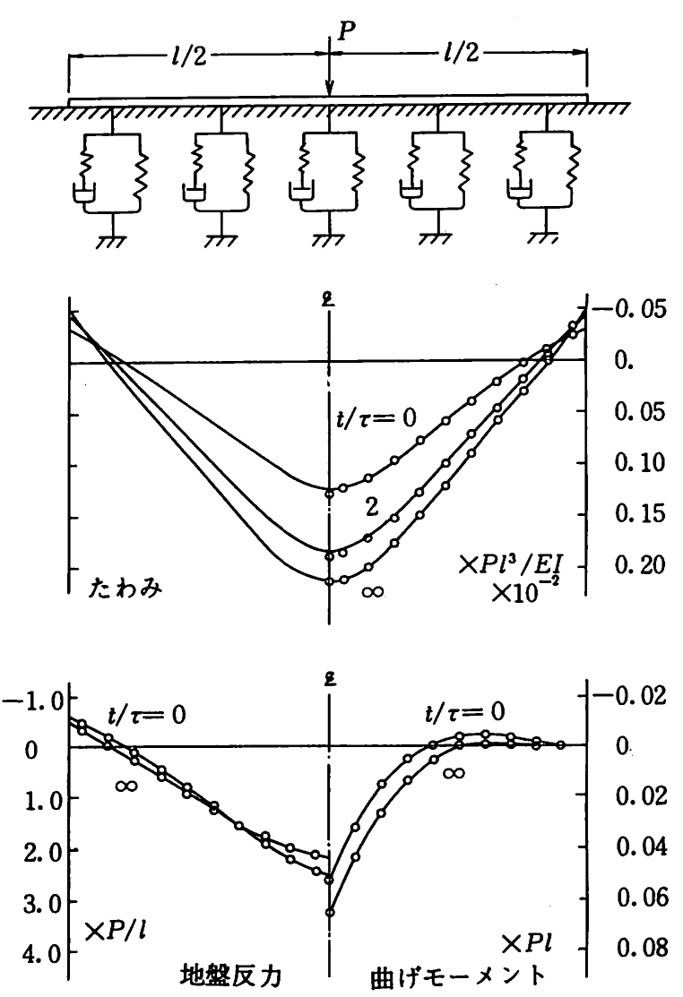
$\hspace{1em}$図8.23 Standard Solidモデルの解析結果
この点をさらに詳細に調べるため、中央点における梁のたわみ、曲げモーメントならびに地盤反力の誤差と分割数の関係を
図8.24に示す。図はKelvinモデルの場合で、その他のモデルもほぼ同じ傾向が生じている。どの誤差も数％以内であり、工学的には十分満足のゆく結果となっている。
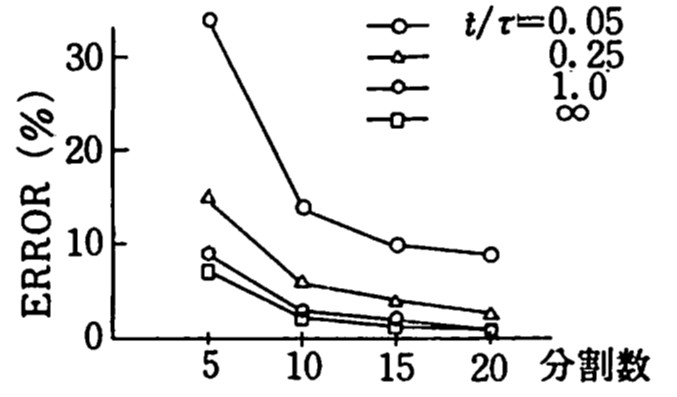
$\hspace{6em}$(a) たわみ
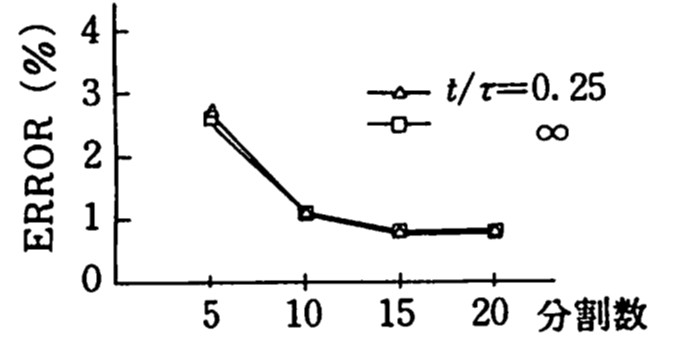
$\hspace{6em}$(b) 地盤反力
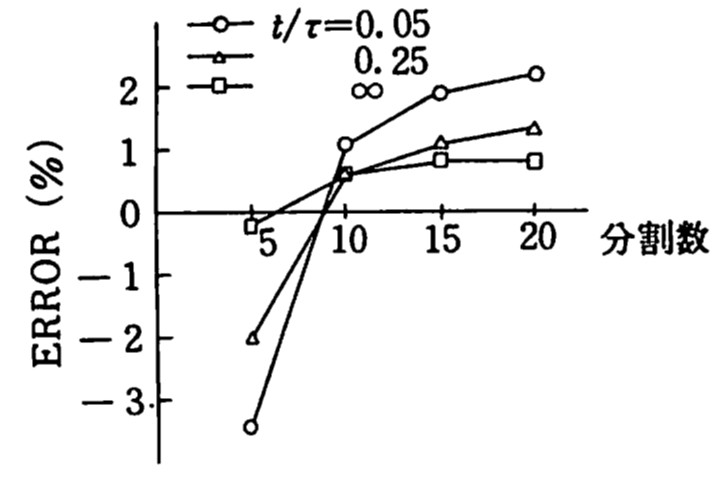
$\hspace{6em}$(c) 曲げモーメント
$\hspace{2em}$図8.24 Kelvinモデルの精度
弾塑性体では、時間の影響を考慮していないため、載荷直後直ちに塑性平衡状態になる。しかし、実際の地盤では、載荷速度を変化させて作用させた場合、急速に載荷した方が緩やかに載荷した場合より初期の段階で大きな荷重まで載荷できることもあり、また、回復できないクリープ変形が発生することも希ではない。このような場合、粘塑性モデルが利用される。このモデルは弾塑性と粘弾性の両者の性質を兼ね備えたようなモデルである。いま、塑性をスライダーで表せば、弾塑性と粘塑性は
図8.25のように表現することができる。ただし、ここで示した
粘塑性モデルは地盤が降伏した後、線形クリープ現象を示す
Bingham型の簡単なモデルである。
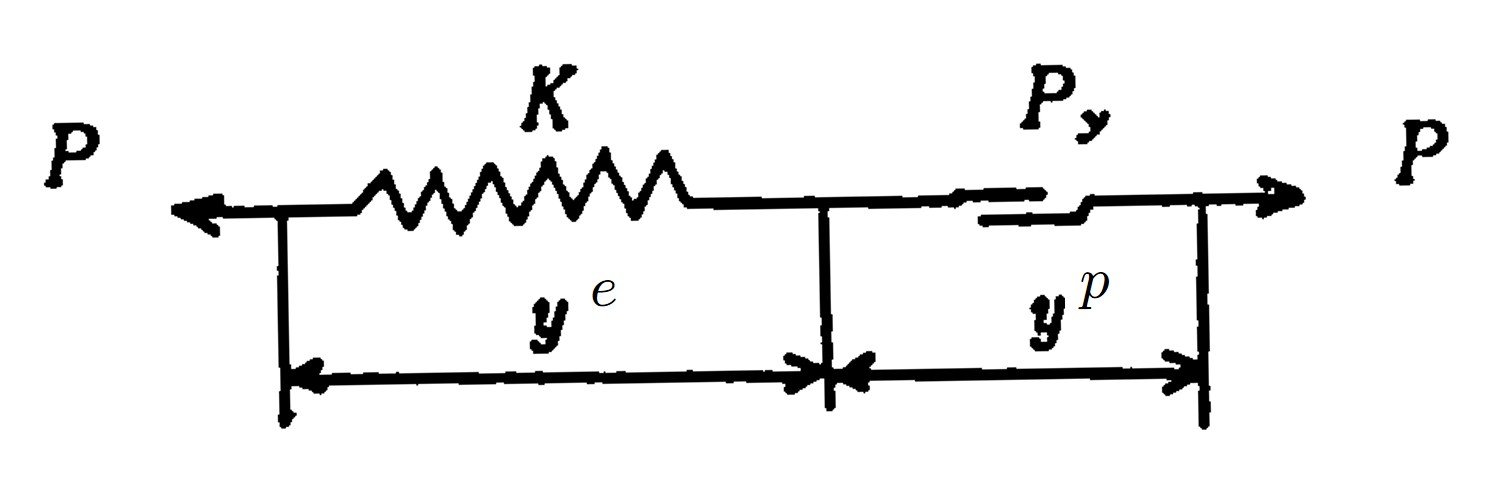
$\hspace{6em}$(a) 弾塑性モデル
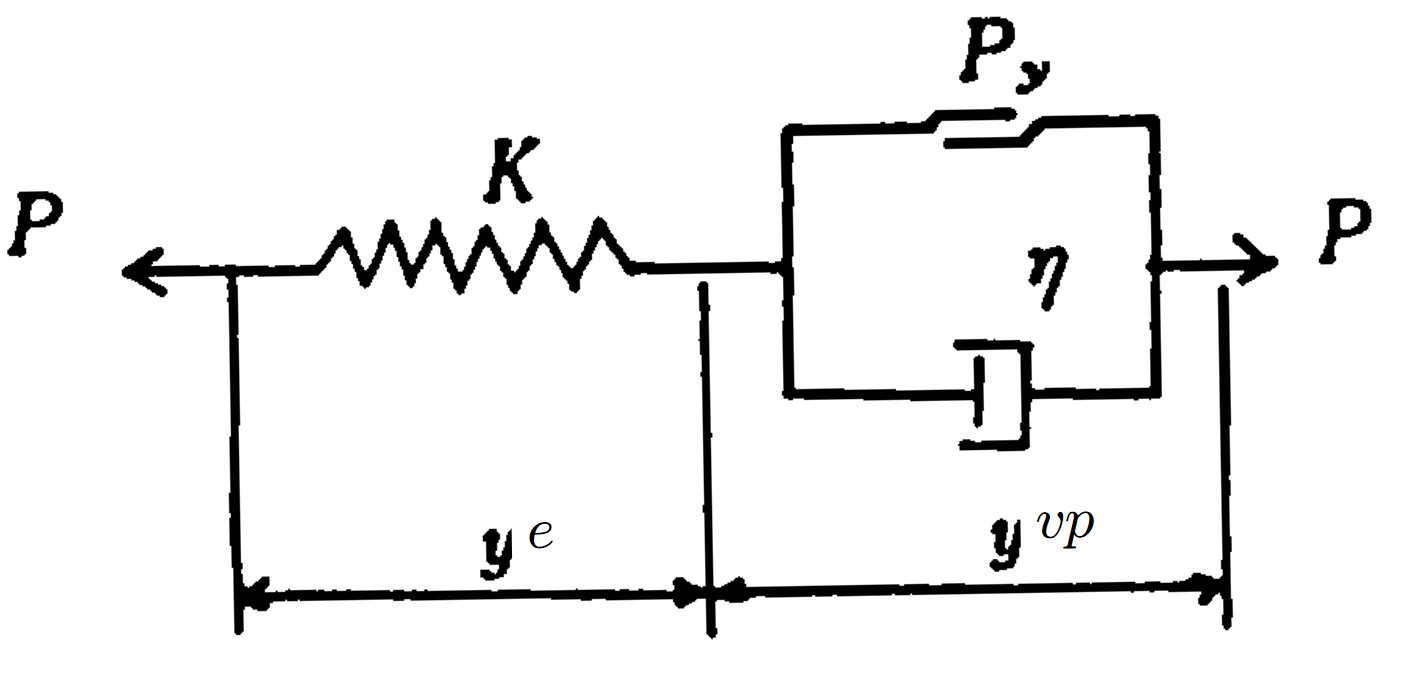
$\hspace{6em}$(b) 粘塑性モデル
\hspace{4em}$図8.25 弾塑性モデルと粘塑性モデル
次に、この Binghamモデルの定式化を行ってみよう。いま、全たわみ増分量 $\Delta y$ は弾性たわみ増分 $(\Delta ^e)$ と粘塑性たわみ増分 $(\Delta y^{vp})$ の和で表すことができる。
\[{\rm (8.25)}
\dot{y} = \dot{y}^{e} + \dot{y}^{vp}
\]
ここで、$k$ をばね定数とすれば、弾性たわみ増分は
\[{\rm (8.26)}
\dot{y}^{e} = \frac{ \dot{P} }{k}
\]
である。一方、粘塑性たわみ増分は $\eta$ を粘性係数として
\[{\rm (8.27)}
\dot{y}^{vp} = \frac{ \lt P-P_{y} \gt }{ \eta }
\]
\[\hspace{6em}
\lt P-P_{y} \gt =
\left \{
\begin{array}{ll}
0 & |P_{y}| \geq |P| \\
P-P_{y} & |P_{y}| \lt |P|
\end{array}
\right.
\]
となる。ただし、$P_y$ は地盤の降伏強度を表すものとする。
以上の結果、
式(8.26)、式(8.27)の関係を
式(8.25)に代入し、差分表示すると
\[{\rm (8.28)}
\Delta P = k \cdot \Delta y - \lt P-P_{y} \gt \frac{k \Delta t}{ \eta }
\]
となる。ここで、$\Delta t$ は増分時間であり、$\Delta P$ は増分荷重、$\Delta y$ は増分たわみを表している。
さて、粘弾性体の場合と同様、増分仮想仕事式
\[{\rm (8.29)}
\Delta \boldsymbol{u}^{*} \cdot \Delta \boldsymbol{F}
= \int ( \Delta y^{*} \cdot \Delta P ) dx
\]
\[\hspace{9em}
= \Delta \boldsymbol{u}^{*} \int
\boldsymbol{B}^t k \boldsymbol{B} dx \Delta \boldsymbol{u}
- \Delta \boldsymbol{u}^{*} \int
\boldsymbol{B}^t \lt P-P_{y} \gt k \frac{ \Delta t}{ \eta } dx
\]
より、以下のが得られる。
\[{\rm (8.30)}
\Delta \boldsymbol{F} =
\int \boldsymbol{B}^{t} k \boldsymbol{B} dx \Delta \boldsymbol{u}
- k \frac{ \Delta t}{ \eta } \int \boldsymbol{B}^{t} \lt P-P_{y} \gt dx
\]
このようにして得られた式に初期ひずみ法を適用することで、任意時刻における解を得ることができる。
数値計算例として、地中の単杭の問題をとり挙げてみた。
図8.26に解析に用いたモデルと材料定数を示す。地盤は粘性地盤を想定し、極限地盤反力分布についてはBromsによる仮定を用いた。また、長い杭と短い杭では破壊パターンが異なることも予想されるため、3mと6mの２通りを考えた。
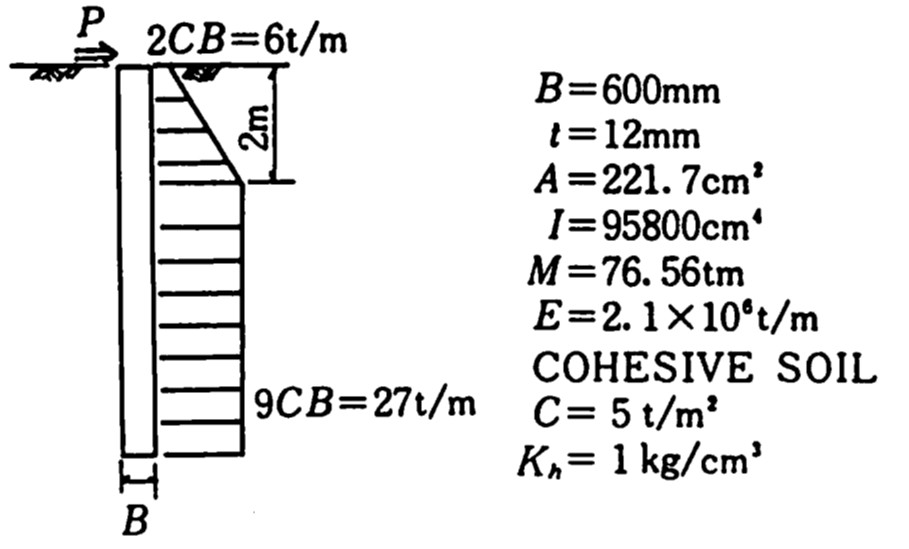
$\hspace{1em}$図8.26 計算に用いたモデルと材料定数
図8.27は短い杭の杭頭における変位を縦軸に、また、時間を横軸にとり示したものである。図中、実線が荷重値P=10tの場合、一点破線が20t、点線が30tの場合である。通常の弾塑性解析によれば、P=21tで地盤の崩壊により杭構造はメカニズムを形成するが、図を眺めると、P=30tの場合、塑性流動が発生しており、この関係と合致する。
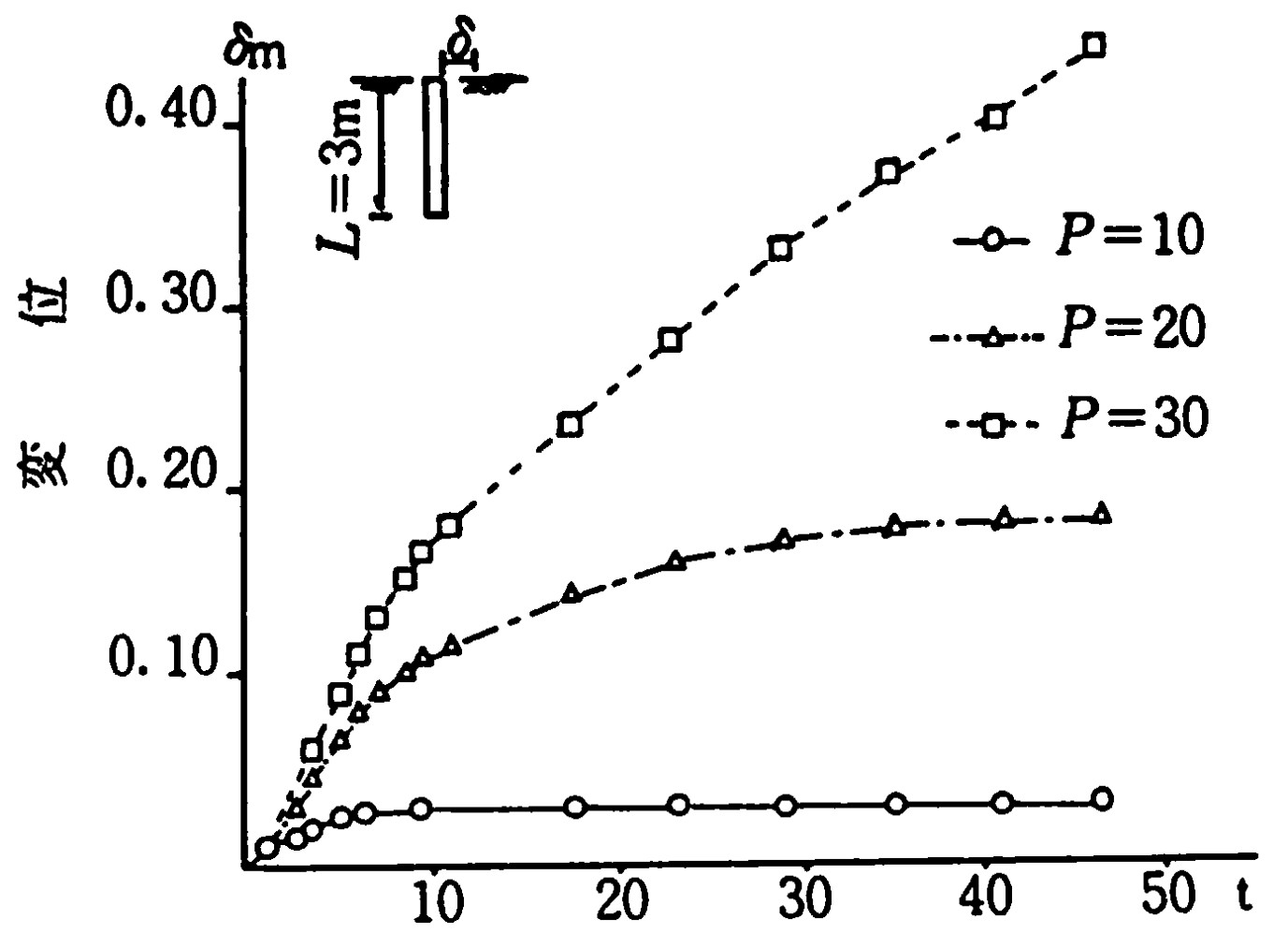
$\hspace{2em}$図8.27 短い杭の荷重－変位曲線
一方、長い杭について同じように整理した結果が
図8.28に示されている。弾塑性解析ではP=51tで杭に塑性ヒンジが発生し崩壊している。図を眺めると、P=50tでは杭に塑性ヒンジは発生せず収束する傾向にあるが、P=55tでは、杭に塑性ヒンジが生じ、塑性流動を起こしている。
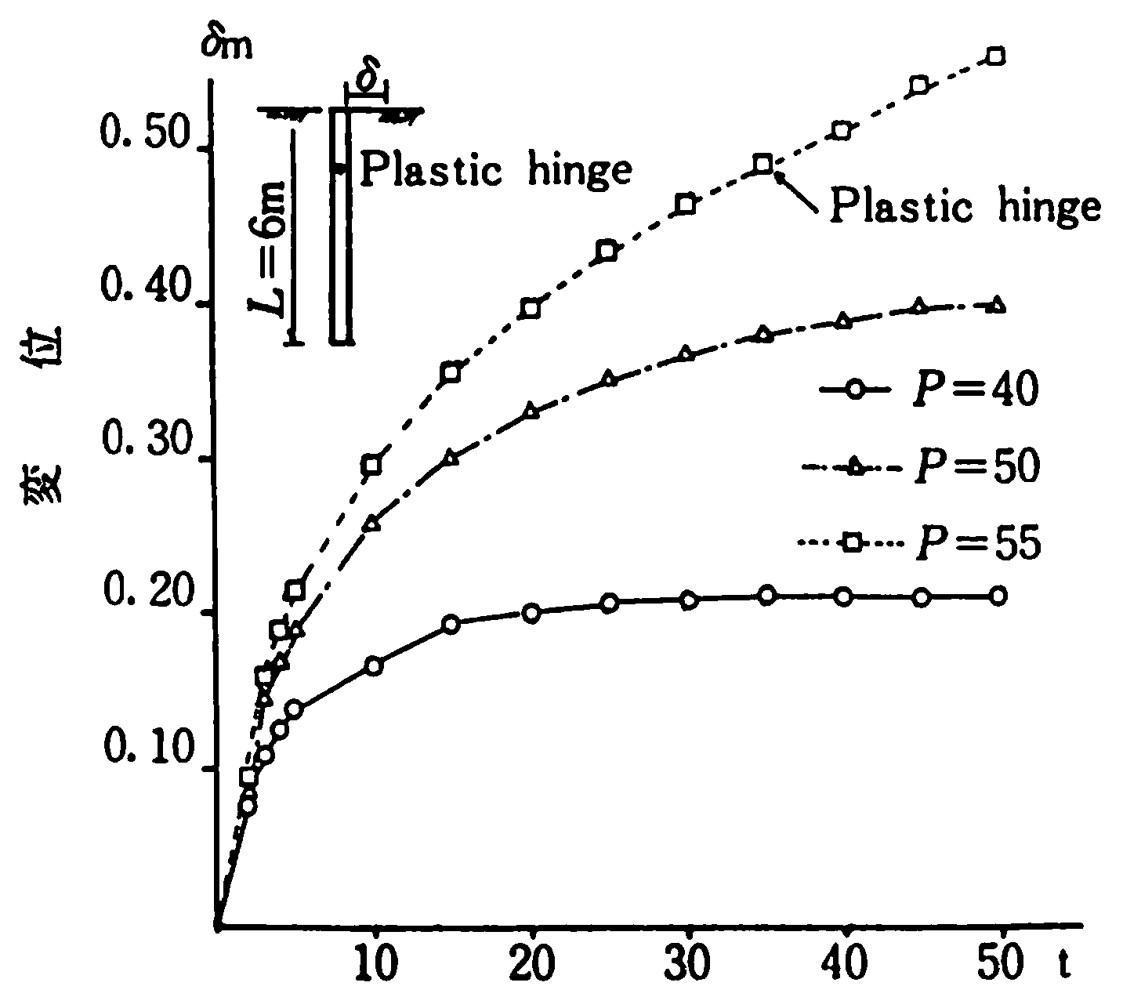
$\hspace{2em}$図8.28 長い杭の荷重－変位曲線
このように、粘塑性地盤を仮定することで、経時的な解析が行えるようになるため、仮設構造物などの計測データーと比較検討することが容易になる。ただし、どのようなタイプの粘塑性モデルを利用するかについては十分な検討が必要である。
平面状態に対する動的問題の取り扱いについては
7章においてすでに述べた。ここでは骨組み構造や地盤を考慮した梁に対する動的解析の方法について説明する。
図8.29は面内変形の梁を表した図で、この関係を用いると梁要素の運動エネルギー $(T)$ は
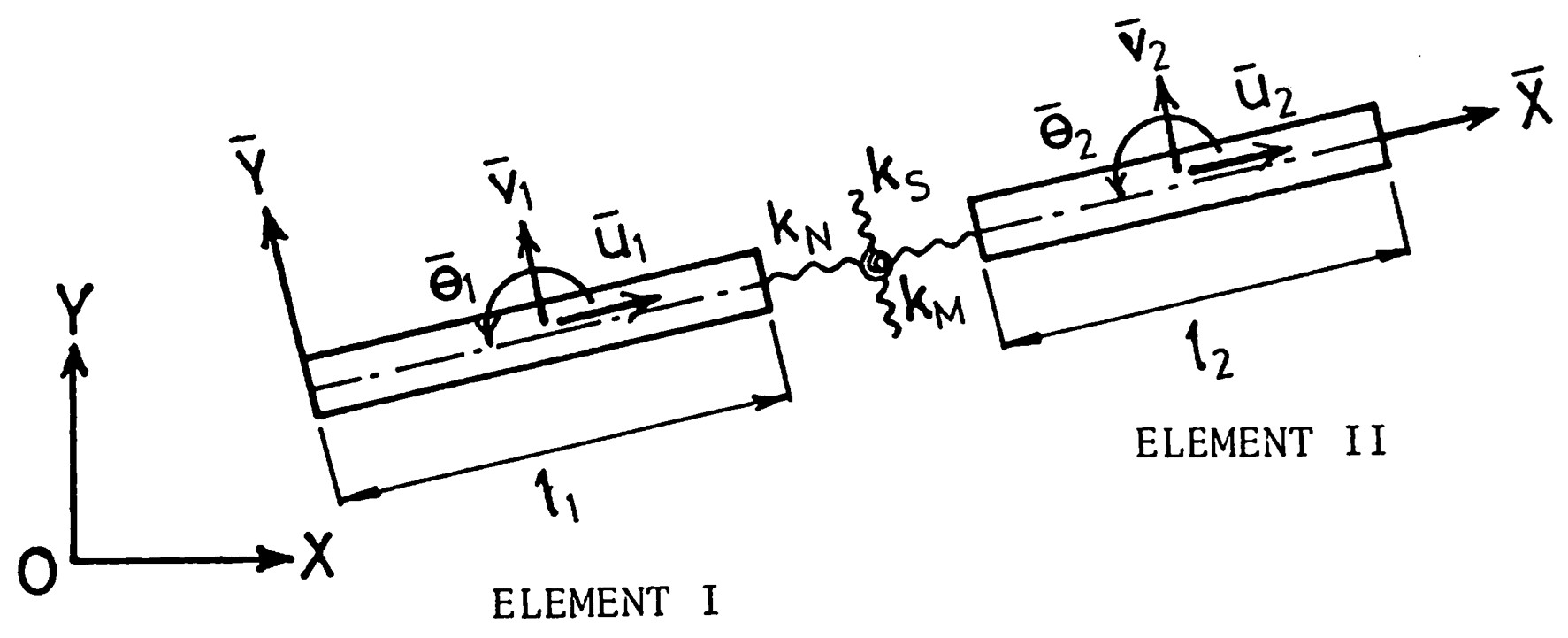
$\hspace{10em}$図8.29 梁要素
\[{\rm (8.31)}
T = \frac{1}{2} \dot{\boldsymbol{u}}^{t} \cdot \boldsymbol{M} \cdot \dot{\boldsymbol{u}}
\]
と表すことができる。ここで、ｕは速度ベクトル、Ｍは質量行列を表しており、それぞれ、以下に示す通りである。
\[\hspace{4em}
\boldsymbol{M} = m
\left[
\begin{array}{ccc}
l & & \\
& l & \\
& & \frac{l^{3}}{12}
\end{array} \right] \;, \;\;\;
\dot{\boldsymbol{u}}^{t} = ( \dot{u} \;\; \dot{v} \;\; \dot{ \theta } )
\]
ただし、$m$ は梁の質量を表している。また、梁要素に関する全ポテンシャルエネルギー $(V)$ は
\[{\rm (8.32)}
V = \frac{1}{2} \boldsymbol{u}^{t} \cdot \boldsymbol{K} \cdot \boldsymbol{u}
- \boldsymbol{u}^{t} \cdot \boldsymbol{F}
\]
であり、剛性行列 $\boldsymbol{K}$ は
9章に示す通りである。一方 Winkler型の地盤ばねを仮定した場合の地盤反力に関するポテンシャルエネルギー $(V_f)$ は
\[{\rm (8.33)}
V_{f} = \frac{1}{2} \boldsymbol{u}^{t} \cdot \boldsymbol{k} \cdot \boldsymbol{u}
\]
である。ここで、$\boldsymbol{k}$ は以下に示す通りである。
\[\hspace{4em}
\boldsymbol{k} = k
\left[
\begin{array}{ccc}
0 & & \\
& l & \\
& & \frac{l^{3}}{12}
\end{array} \right]
\]
ミルトンの原理によれば、
\[{\rm (8.34)}
\delta \int ( T-V-V_{f} ) dt = 0
\]
であり、この変分問題に対応するオイラーの方程式は
\[{\rm (8.35)}
\boldsymbol{M} \cdot \ddot{\boldsymbol{u}}
+ ( \boldsymbol{K} + \boldsymbol{k} ) \boldsymbol{u} = \boldsymbol{F}
\]
となる。
この方程式の数値計算法に関しては、平面要素の場合と同様であり、従来の方法をそのまま利用することができる。ただし、川井モデルの梁要素の場合、集中荷重作用位置や隅角部、あるいは境界点において長さも質量も持たないピン要素が利用される。このため、このピン要素に関する質量行列の項が0となり、質量行列の対角項に0が含まれてしまう。そこで、
式(8.36)に示す関係より
\[{\rm (8.36)}
\left[
\begin{array}{cc}
\boldsymbol{M}_{rr} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{0}
\end{array} \right]
\left \{
\begin{array}{c}
\ddot{\boldsymbol{u}_{r}} \\
\ddot{\boldsymbol{u}_{s}}
\end{array} \right \} +
\left[
\begin{array}{cc}
\boldsymbol{K}_{rr} & \boldsymbol{K}_{rs} \\
\boldsymbol{K}_{sr} & \boldsymbol{K}_{ss}
\end{array} \right]
\left \{
\begin{array}{c}
\boldsymbol{u_{r}} \\
\boldsymbol{u_{s}}
\end{array} \right \} =
\left \{
\begin{array}{c}
\boldsymbol{F_{r}} \\
\boldsymbol{F_{s}}
\end{array} \right \}
\]
質量行列の対角項が0の部分を以下のように縮約する。
\[{\rm (8.37)}
\boldsymbol{M}_{rr} \cdot \ddot{\boldsymbol{u}}_{r}
+ \boldsymbol{K}_{nn} \boldsymbol{u}_{r} = \boldsymbol{F}_{n}
\]
\[\hspace{6em}
( \boldsymbol{K}_{nn} = \boldsymbol{K}_{rr}
- \boldsymbol{K}_{rs} \cdot \boldsymbol{K}_{ss}^{-1} \cdot \boldsymbol{K}_{sr} \;,\;\;\;
\boldsymbol{F}_{n} = \boldsymbol{F}_{r}
- \boldsymbol{K}_{rs} \cdot \boldsymbol{K}_{ss}^{-1} \cdot \boldsymbol{F}_{s} )
\]
式(8.35)において、地盤反力の項が無ければ、単純に梁要素のみの運動方程式となっている。以下に簡単な数値計算例によりこの運動方程式を解いて得られる解の性質を調べてみよう。
図8.30(a)は等断面を持つ下端固定の棒をモデル化したものであり、この棒の先端に、
図(b)に示すような正弦波半波形の衝撃荷重を下向きに作用させた場合を考える。これは、杭打ち作業において杭の一端が打撃を受けた場合のモデルを想定している。ただし、解の精度を検証するため厳密解の求まっている簡単なモデルを考えており、杭周辺の摩擦による影響は無視している。
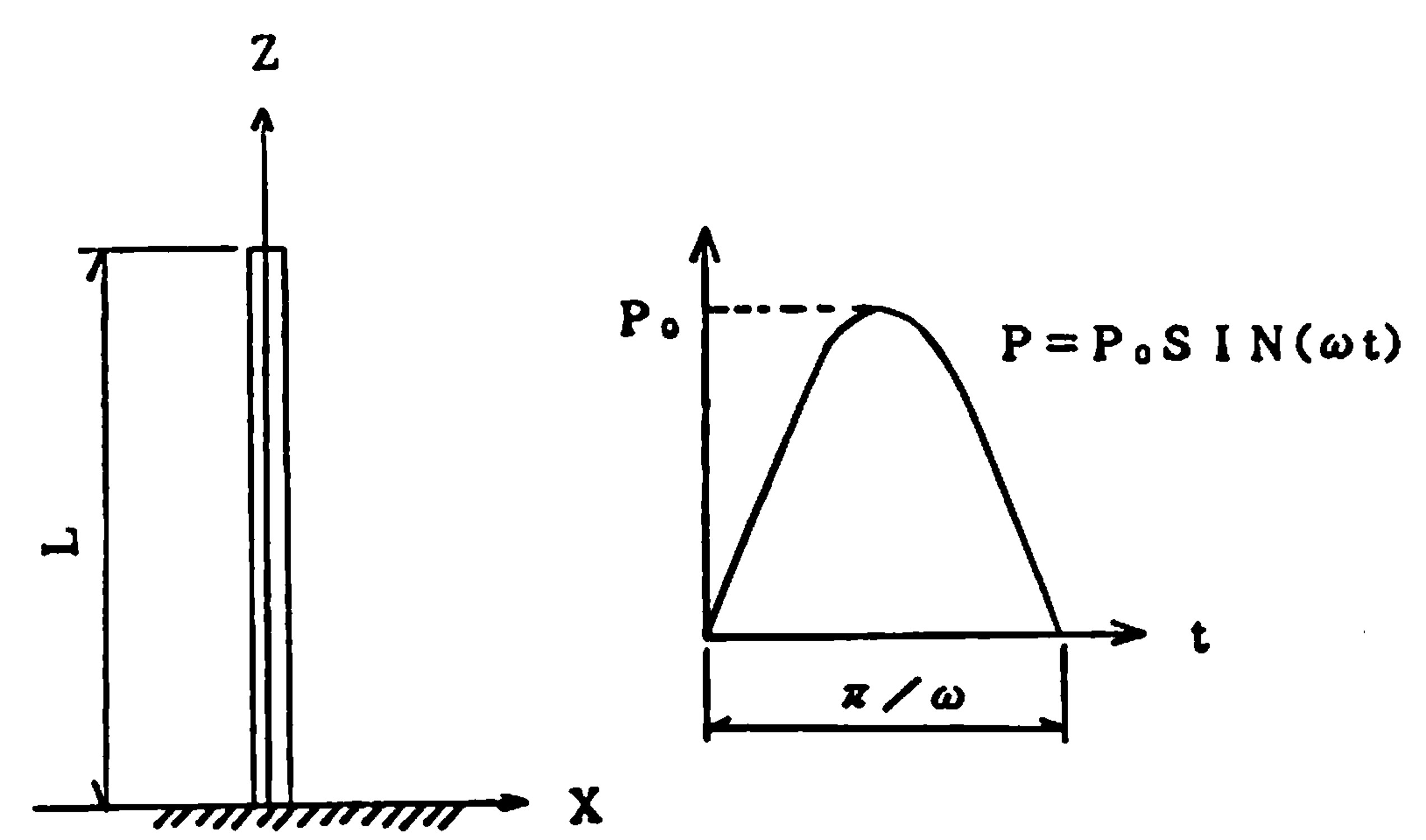
$\hspace{5em}$(a)
$\hspace{8em}$(b)
$\hspace{2em}$図8.30 縦振動解析モデルと衝撃荷重
図8.31は打撃終了時点において、波動論より求めた軸力と変位を本モデルによる解と比較した図である。図中、実線が波動論より求めた厳密解であり、〇が本モデルによる求めた解である。両者を比較すると、軸力、変位とも良好な結果が得られていることが理解できよう。
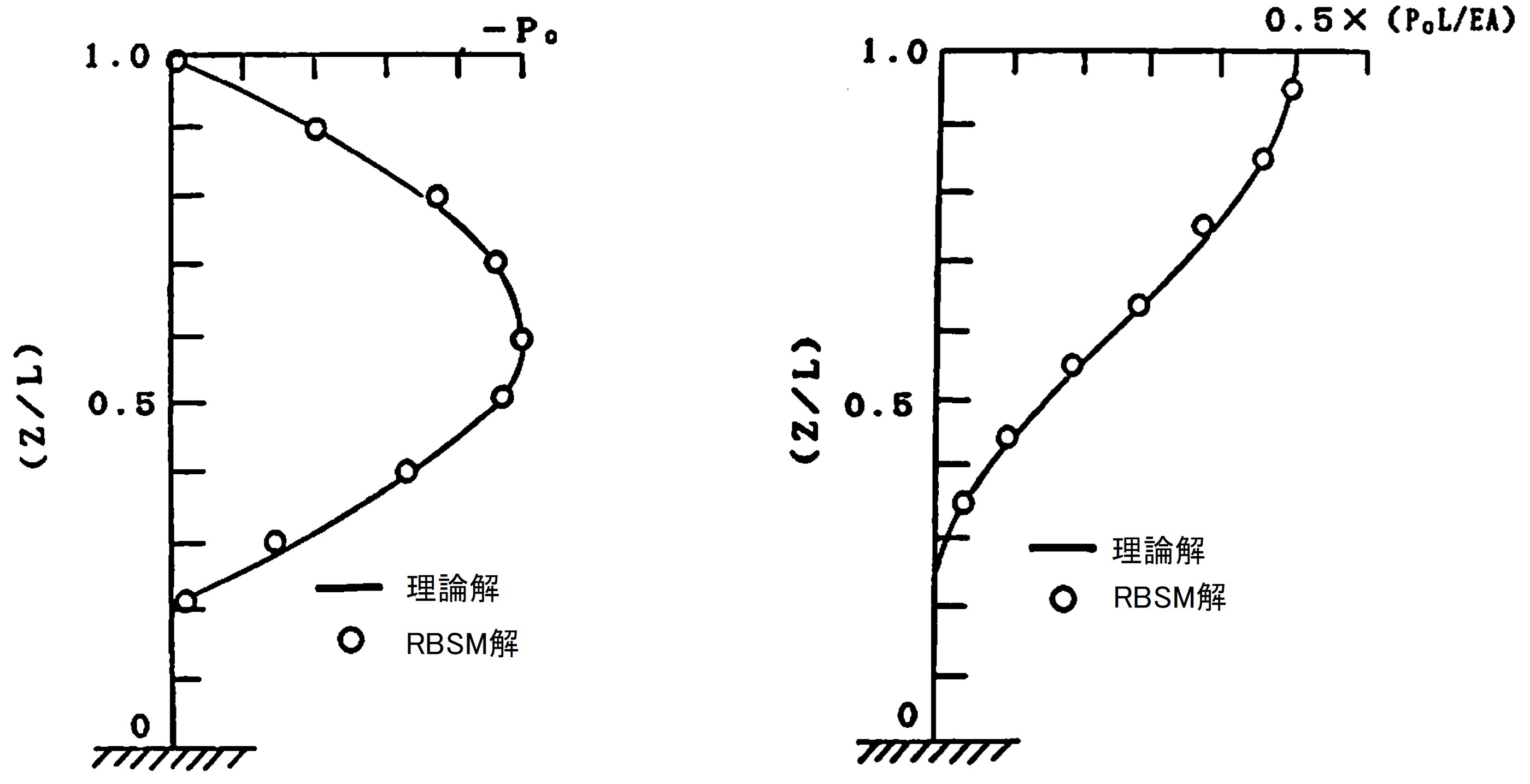
$\hspace{2em}$図8.31 打撃終了時点の軸力と変位
次に地盤を考慮した梁の衝撃崩壊解析例を示そう。
図8.32は配管桟橋に船舶などの浮遊物が衝突した場合を想定して作成したモデルである。地盤に関しては完全弾塑性体とし、極限水平抵抗土圧以上は抵抗しないものとしている。この極限水平抵抗土圧分布についてはBroms の提案した関係を用いた。
図(a)にモデルと材料定数を、また、
図(b)には正弦半波形の衝撃荷重を示している。ただし、この例題もモデルのチェックであるため、厳密には質量の大きな船舶が衝突した荷重状態ではない。
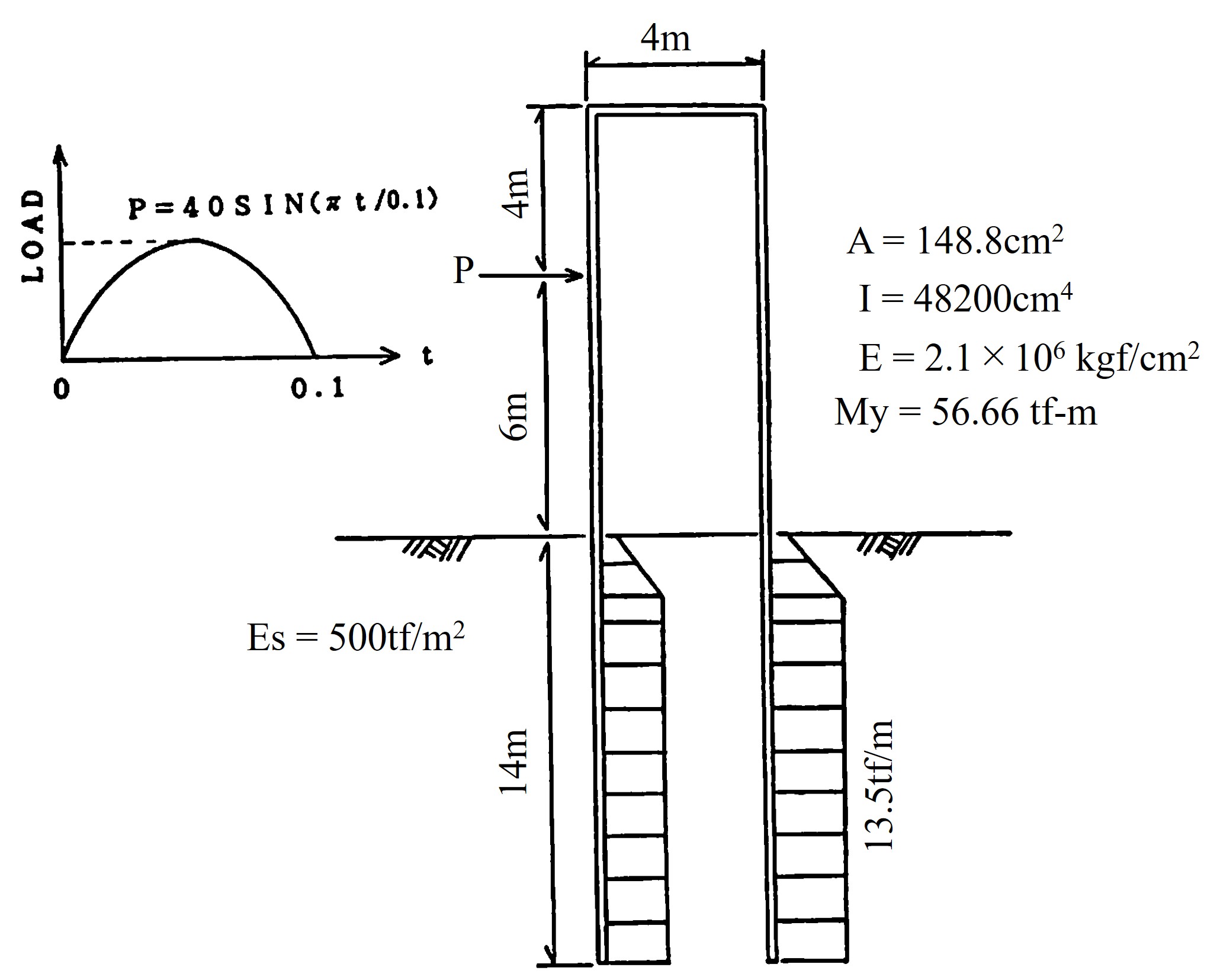
$\hspace{2em}$図8.32 配管桟橋の解析モデルと衝撃荷重
図8.33には静的な弾塑性解析の結果が示されている。図中黒丸により示されている部分はヒンジが発生した部分である。これに対し、
図8.34には打撃終了時点までの各時刻における崩壊状況と曲げモーメント分布が示されている。このように、静的な解析と動的な解析とでは若干相違が見られる。
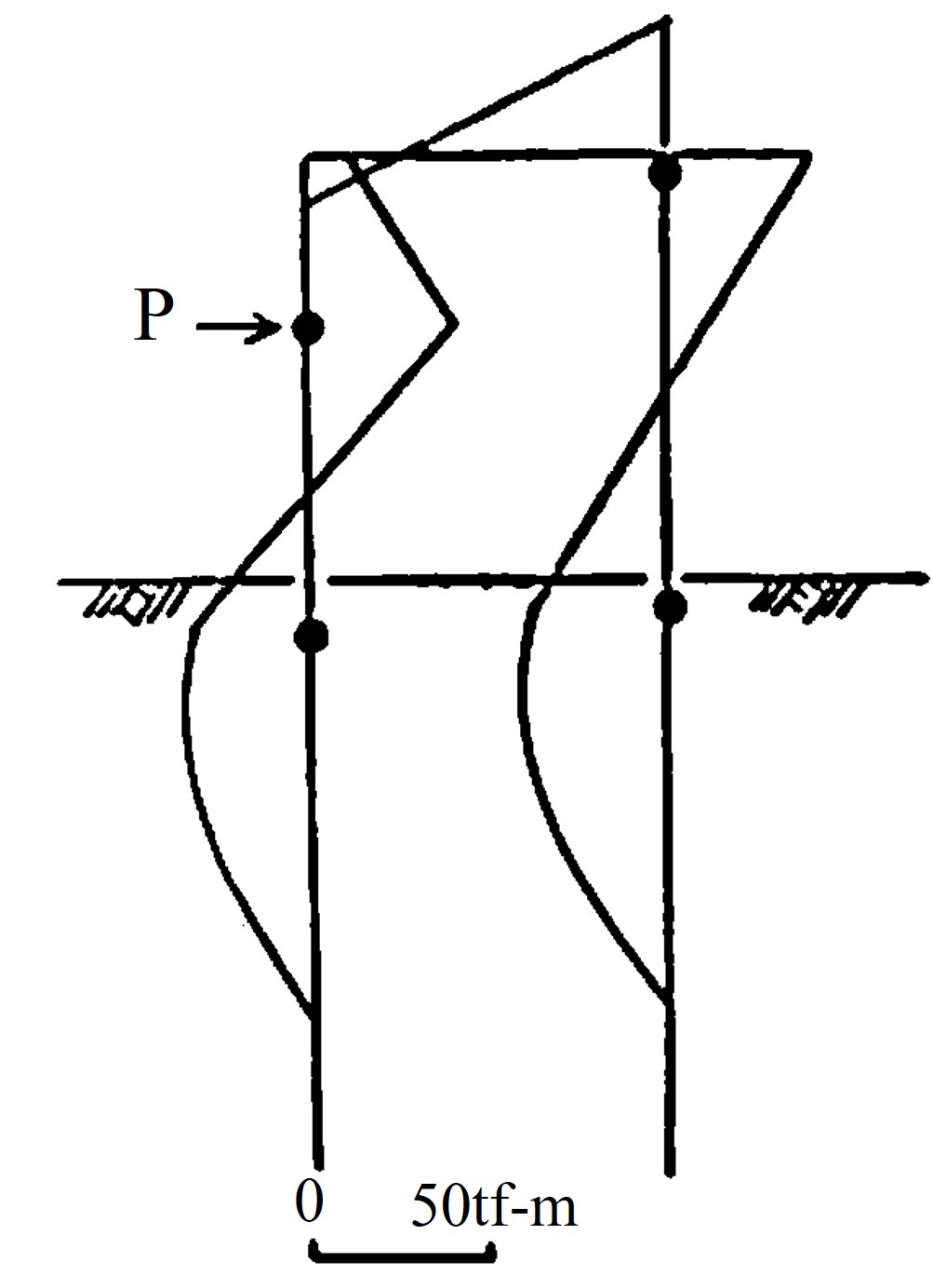
$\hspace{0em}$図8.33 静的弾塑性解析における曲げモーメント
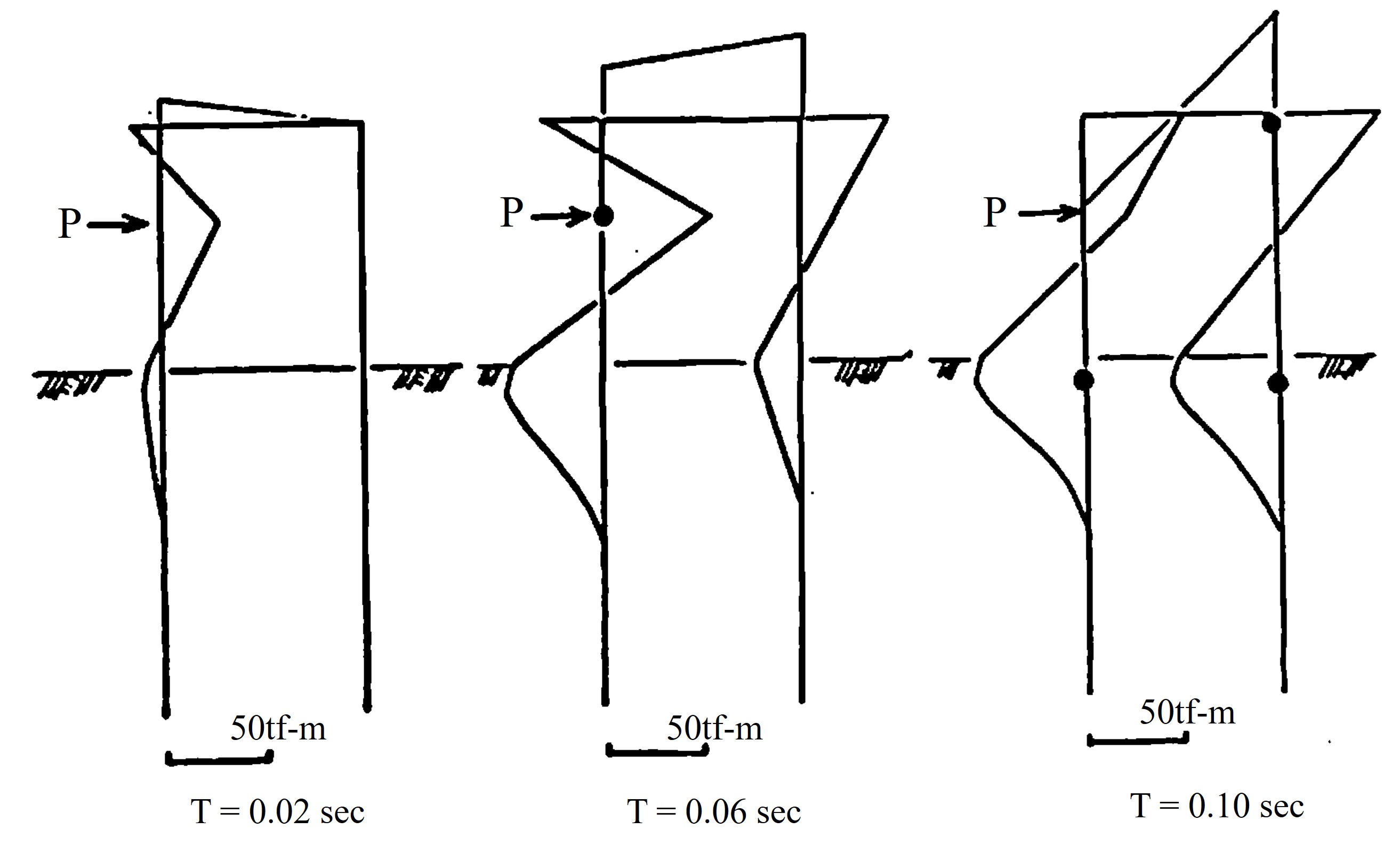
$\hspace{4em}$図8.34 衝撃解析における曲げモーメント
以上、簡単な例により地盤を考慮した骨組構造物の動的崩壊解析の手法を説明した。この方法を用いれば、
7章で説明した平面要素と組み合わせて動的崩壊解析を行うことが可能である。