7.動的問題の解析法
7-1 動的問題の定式化
1自由度系のいま、要素境界辺の増分表面力を $\Delta \boldsymbol{\sigma}$、増分物体力を $\Delta \boldsymbol{f}$ とし、増分仮想相対変位を $\Delta \boldsymbol{\delta}^*$、増分仮想剛体変位を $\Delta \boldsymbol{u}_i^*$ とすれば、動的問題に対する増分仮想仕事式は以下のように表される。 \[{\rm (7.6)} \frac{ \gamma }{ g } \int_{v} \{ ( \Delta \boldsymbol{u}_{i}^{*} ) ^{t} \cdot \Delta \ddot{\boldsymbol{u}}_{i} \} dv + \int_{s} \{ ( \Delta \boldsymbol{\delta}^{*} )^{t} \cdot \Delta \boldsymbol{\sigma} \} ds = \int_{v} \{ ( \Delta \boldsymbol{u}_{i}^{*} )^{t} \cdot \Delta\boldsymbol{F} \} dv \] ここで、$\gamma$ は単位体積重量、$g$ は重力加速度である。
質量行列 $\boldsymbol{M}$ は \[{\rm (7.8)} \boldsymbol{M} = \int_{v} \{ ( \boldsymbol{Q}_i )^{t} \cdot \boldsymbol{Q}_i \} dv \] である。川井モデルの場合、要素重心にパラメーターがあるため、この質量行列は要素単位に作成することができる。また、ばね質点系と同様、重ね合わせの必要もない。各要素モデルに対する質量行列の詳細については、
また、剛性行列$\boldsymbol{K}$は \[{\rm (7.9)} \boldsymbol{K} = \int_{s} ( \boldsymbol{B}^{t} \cdot \boldsymbol{D} \cdot \boldsymbol{B}) ds \] であり、
一方、外力項における物体力は \[{\rm (7.10)} \Delta \boldsymbol{F}_{f} = \int_{v} ( \boldsymbol{Q}_{i} \cdot \Delta \boldsymbol{f}_{i} ) dv \] であり、パラメーターを要素重心に設定すれば、モーメントの項は0となる。例えば、3次元要素の場合の物体力は \[\hspace{4em} \Delta \boldsymbol{F}_{f} = V( \Delta f_{x} \;, \;\; \Delta f_{y} \;, \;\; \Delta f_{z} \;, \;\; 0 \;, \;\; 0 \;, \;\; 0 )^{t} \] となる。ここで、$V$ は要素の体積であり、$\Delta f_x、\Delta f_y、\Delta f_z$ は各方向の増分物体力の成分を表している。外力として、要素重心に作用する増分力 $\Delta \boldsymbol{F}_p$ を考えた場合、例えば3次元では \[{\rm (7.11)} \Delta \boldsymbol{F}_{p} = ( \Delta X \;, \;\; \Delta Y \;, \;\; \Delta Z \;, \;\; \Delta L \;, \;\; \Delta M \;, \;\; \Delta N )^{t} \] となる。また、地震などにおける加速度入力があった場合には、要素重心における増分の地震加速度を $\Delta \boldsymbol{u}_{ig}$として \[{\rm (7.12)} \Delta \boldsymbol{u}_{i}^{*} \cdot \Delta \boldsymbol{F}_{m} = - \frac{ \gamma }{g} \int_{v} \{ (\Delta \boldsymbol{u}_i^* )^t \cdot \Delta \ddot{\boldsymbol{u}}_{ig} \} dv \] といった仮想仕事式を、
したがって、
次に減衰について考えてみよう。減衰行列にもいろいろな方法が考えられるが、ここではレイリー減衰について説明する。レイリー減衰では減衰行列 $\boldsymbol{C}$ を質量行列 $\boldsymbol{M}$ と剛性行列 $\boldsymbol{K}$ の線形和として \[{\rm (7.16)} \boldsymbol{C} = \alpha_{0} \boldsymbol{M} + \alpha_{1}\boldsymbol{ K} \] のよう仮定する。ここで、係数 $\alpha_0$、$\alpha_1$ の値は全体系の1次、2次の固有円振動数 $\omega_1$、$\omega_2$ より \[{\rm (7.17)} \alpha_{0} = 2 \omega_{1} \omega_{2} \frac{ h_{2} \omega_{2} - h_{1} \omega_{1}} { \omega_{2}^{2} - \omega_{1}^{2} } \;, \;\;\; \alpha_{1} = 2 \frac{ h_{2} \omega_{2} - h_{1} \omega_{1}} { \omega_{2}^{2} - \omega_{1}^{2} } \] と求める。上式において、$h_1、h_2$ は1次および2次の減衰係数である。以上の減衰効果を含めれば最終的に解くべき運動方程式は \[{\rm (7.18)} \boldsymbol{M} \cdot \Delta \boldsymbol{\ddot{u}} + \boldsymbol{C} \cdot \Delta \boldsymbol{\dot{u}} + \boldsymbol{K} \cdot \Delta \boldsymbol{u} = \Delta \boldsymbol{F} \] \[\hspace{6em} ( \Delta \boldsymbol{F} = \Delta \boldsymbol{F}_{f} + \Delta \boldsymbol{F}_{p} + \Delta \boldsymbol{F}_{m}) \] となる。
7-2 運動方程式の数値計算法
運動方程式の解析法としては前節において、運動中の系に対する平衡方程式 \[{\rm (7.19)} \boldsymbol{M} \cdot \ddot{\boldsymbol{u}} + \boldsymbol{C} \cdot \dot{\boldsymbol{u}} + \boldsymbol{K} \cdot \boldsymbol{u} = \boldsymbol{F} \] を導いた。おのおのの係数行列は有限要素法などの場合と異なっているものの、数値積分の立場から考えると、アルゴリズム的に有限要素法などの数値解析法と同様に扱うことができる。ここでは、このような理由により、代表的な直接積分法であるNewmark のβ法による計算法についてのみ説明する。
一般にNewmarkのβ法の公式は以下のように書くことができる。 \[{\rm (7.20)} \left. \begin{array}{rcl} \dot{u}_{i+1} & = & \dot{u}_{i} + \frac{1}{2}( \ddot{u}_i + \ddot{u}_{i+1} ) \Delta t \\[0.5em] u_{i+1} & = & u_{i} + \dot{u}_{i} \Delta t + \frac{1}{2} \ddot{u}_{i} \Delta t^{2} + \beta ( \ddot{u}_{i+1} - \ddot{u}_{i} ) \Delta t^{2} \end{array} \right\} \] ここで、$\Delta t$ は増分時間で、下付きの添字は時間ステップを表し、$(i)$ が現在の時間 $t$、$(i+1)$ が現在の時間から $\Delta t$ 後の値であることを意味している。$\beta$ は陰陽の程度を調整するパラメーターで、$\beta = 0$ のとき陽公式、となり、$\beta = 1/2$ のとき陰公式となる。また、$\beta=1/6$ のとき線形加速度法と一致し、Taylor展開の3次項までを考慮したことになる。$\beta=1/4$ とした場合は平均加速度法と呼ばれている。
次に、このβ法を用いた計算アルゴリズムについて説明しよう。解析法としては、変位増分を求めた後、速度増分、加速度増分を求める方法と、加速度増分を求めた後、変位増分と速度増分を求める2つの方法が考えられる。まず、変位増分を求める方法から説明しよう。
- 1)変位、速度、加速度に初期値を設定する。
- 2)係数行列$\boldsymbol{M}$、$\boldsymbol{K}$、$\boldsymbol{C}$を作成する。
- 3)以下の式を解いて変位増分を求める。 \[\hspace{2em}{\rm (7.21)} \Delta \boldsymbol{u} = \left[ \frac{1}{\beta \Delta t^2 } \boldsymbol{M} + \frac{1}{ 2 \beta \Delta t } \boldsymbol{C} + \boldsymbol{K} \right]^{-1} \] \[\hspace{10em} \times \left[ \boldsymbol{M} \left( \frac{1}{ \beta \Delta t} \dot{\boldsymbol{u}}_i + \frac{1}{ 2 \beta} \ddot{\boldsymbol{u}}_i \right) + \boldsymbol{C} \left\{ \frac{1}{ 2 \beta} \dot{\boldsymbol{u}}_{i} + \left( \frac{1}{4 \beta} - 1 \right) \Delta t \cdot \ddot{\boldsymbol{u}}_i \right\} + \Delta \boldsymbol{F} \right] \]
- 4)以下の式により速度増分を求める。 \[\hspace{2em}{\rm (7.22)} \Delta \dot{\boldsymbol{u}} = \Delta t \cdot \ddot{\boldsymbol{u}}_{i} + \frac{1}{2 \beta \Delta t } \left\{ \Delta \boldsymbol{u} - \Delta t \cdot \dot{\boldsymbol{u}}_{i} - \frac{ \Delta t^{2}}{2} \ddot{\boldsymbol{u}}_{i} \right\} \]
- 5)以下の式により加速度増分を求める。 \[\hspace{2em}{\rm (7.23)} \Delta \ddot{\boldsymbol{u}} = \frac{1}{ \beta \Delta t^{2}} \left\{ \Delta \boldsymbol{u} - \Delta t \cdot \dot{\boldsymbol{u}}_{i} - \frac{ \Delta t^{2}}{2} \ddot{\boldsymbol{u}}_{i} \right\} \]
- 6)前回までの値に増分量を以下のように加え合わせ、今回の値とする。 \[\hspace{2em}{\rm (7.24)} \left. \begin{array}{lcr} \boldsymbol{u}_{i+1} & = & \boldsymbol{u}_i + \Delta \boldsymbol{u} \\ \dot{\boldsymbol{u}}_{i+1} & = & \dot{\boldsymbol{u}}_i + \Delta \dot{\boldsymbol{u}} \\ \ddot{\boldsymbol{u}}_{i+1} & = & \ddot{\boldsymbol{u}}_i + \Delta \ddot{\boldsymbol{u}} \end{array} \right\} \]
次に、加速度増分を初めに求める方について説明しよう。
- 1)変位、速度、加速度に初期値を設定する。
- 2)係数行列 $\boldsymbol{M}$、$\boldsymbol{K}$、$\boldsymbol{C}$ を作成する。
- 3)以下の式を解いて加速度増分を求める。 \[\hspace{2em}{\rm (7.25)} \Delta \ddot{\boldsymbol{u}} = \left[ \boldsymbol{M} + \frac{ \Delta t }{2}\boldsymbol{C} + \beta \Delta t ^{2}\boldsymbol{K} \right]^{-1} \left\{ \Delta \boldsymbol{F} - \Delta t \cdot \boldsymbol{C} \ddot{\boldsymbol{u}}_{i} - \boldsymbol{K} \left( \Delta t \cdot \dot{\boldsymbol{u}}_{i} + \frac{ \Delta t^{2}}{2} \ddot{\boldsymbol{u}}_{i} \right) \right\} \]
- 4)(2)の結果を利用し、以下のように変位増分を求める。 \[\hspace{2em}{\rm (7.26)} \Delta \boldsymbol{u} = \Delta t \cdot \dot{\boldsymbol{u}}_{i} + \frac{ \Delta t^{2}}{2} \ddot{\boldsymbol{u}}_{i} + \beta \Delta t^{2} \cdot \Delta \ddot{\boldsymbol{u}} \]
- 5)以下の式により速度増分を求める。 \[\hspace{2em}{\rm (7.27)} \Delta \dot{\boldsymbol{u}} = \Delta t \cdot \ddot{\boldsymbol{u}}_{i} + \frac{ \Delta t}{2} \Delta \ddot{\boldsymbol{u}} \]
- 6)前回までの値に増分量を以下のように加え合わせ、今回の値とする。 \[\hspace{2em}{\rm (7.28)} \left. \begin{array}{lcr} \boldsymbol{u}_{i+1} & = & \boldsymbol{u}_i + \Delta \boldsymbol{u} \\ \dot{\boldsymbol{u}}_{i+1} & = & \dot{\boldsymbol{u}}_i + \Delta \dot{\boldsymbol{u}} \\ \ddot{\boldsymbol{u}}_{i+1} & = & \ddot{\boldsymbol{u}}_i + \Delta \ddot{\boldsymbol{u}} \end{array} \right\} \]
以上、Newmark のβ法について説明を行ったが、有限要素法などの従来の計算法と何ら相違がないことに気づかれたであろう。初めにも述べたように、他の直接積分法もこのNewmarkのβ法と同様、アルゴリズム的には有限要素法と同じである。
7-3 簡単な斜面安定解析法
斜面安定問題の解析例を示す前に、簡単なモデルにより固有値解析を行った結果を示そう。モデルとして、無限に広がる水平地盤が一様なせん断固有振動をする場合を取り上げた。このような場合、単位幅の地盤を取り出して解析することができ、せん断型連続体振動論により理論解が求まってる。ここでは、川井モデルによる解とこの理論解ならびに有限要素法による解を比較してみる。解析に用いたモデルおよび要素分割パターンが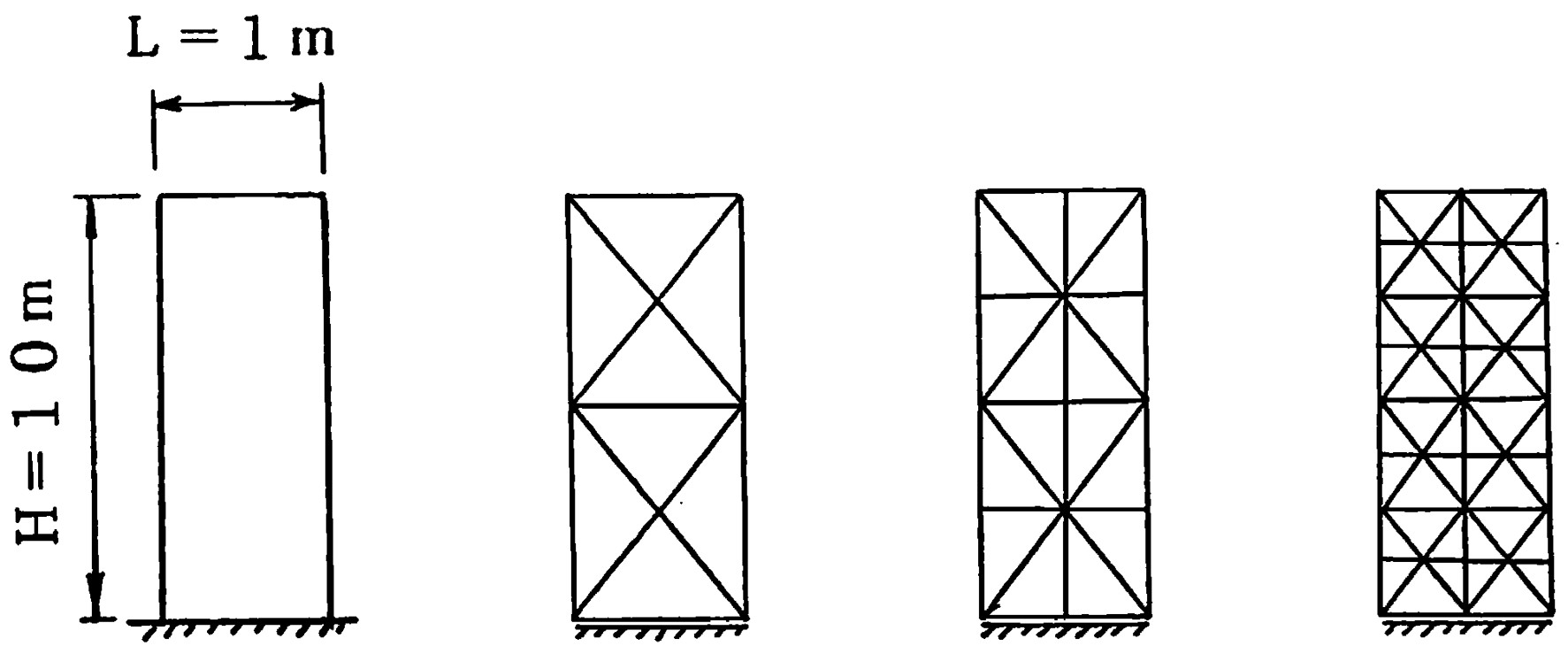
$\hspace{6em}$
| 次数 | 理論解 | 本モデル | 有限要素法 | ||||
|---|---|---|---|---|---|---|---|
| (8要素) | (16要素) | (32要素) | (8要素) | (16要素) | (32要素) | ||
| 1次 | 0.81 | 0.76 | 0.79 | 0.79 | 0.81 | 0.81 | 0.81 |
| 2次 | 0.27 | 0.22 | 0.25 | 0.26 | 0.29 | 0.28 | 0.27 |
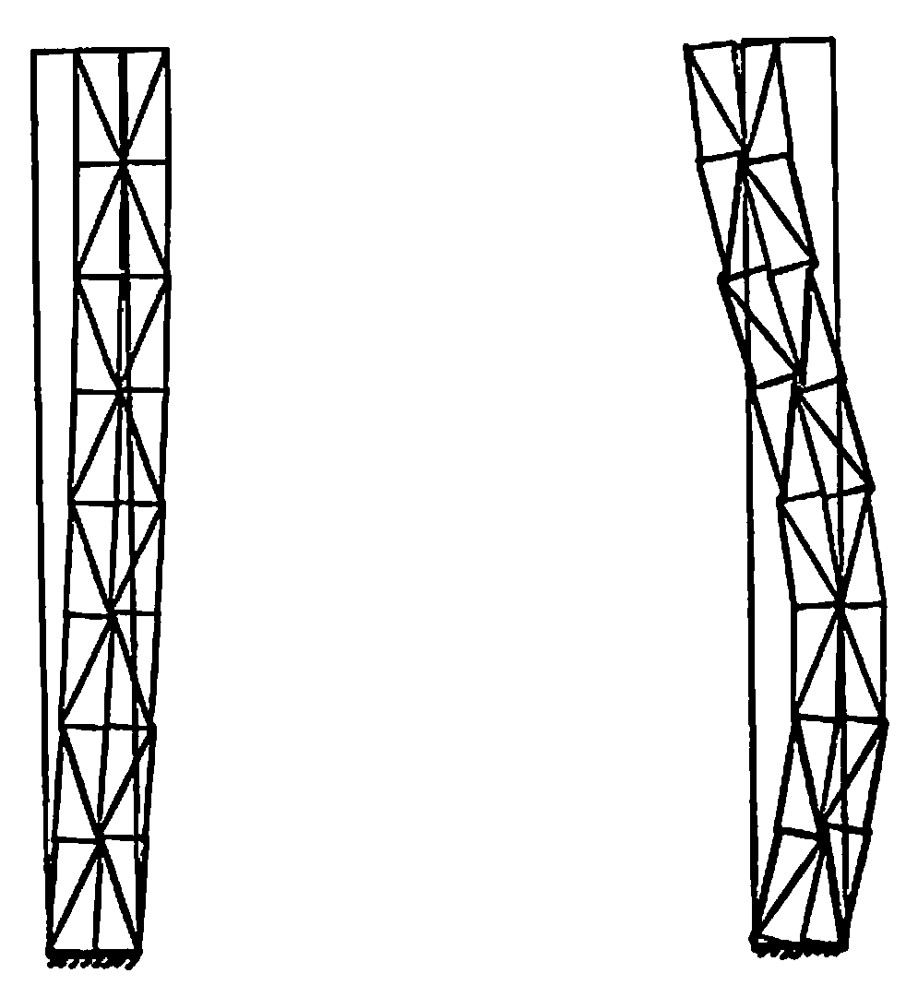
$\hspace{0em}$
この種の問題において、従来法における安全率と比較するためには
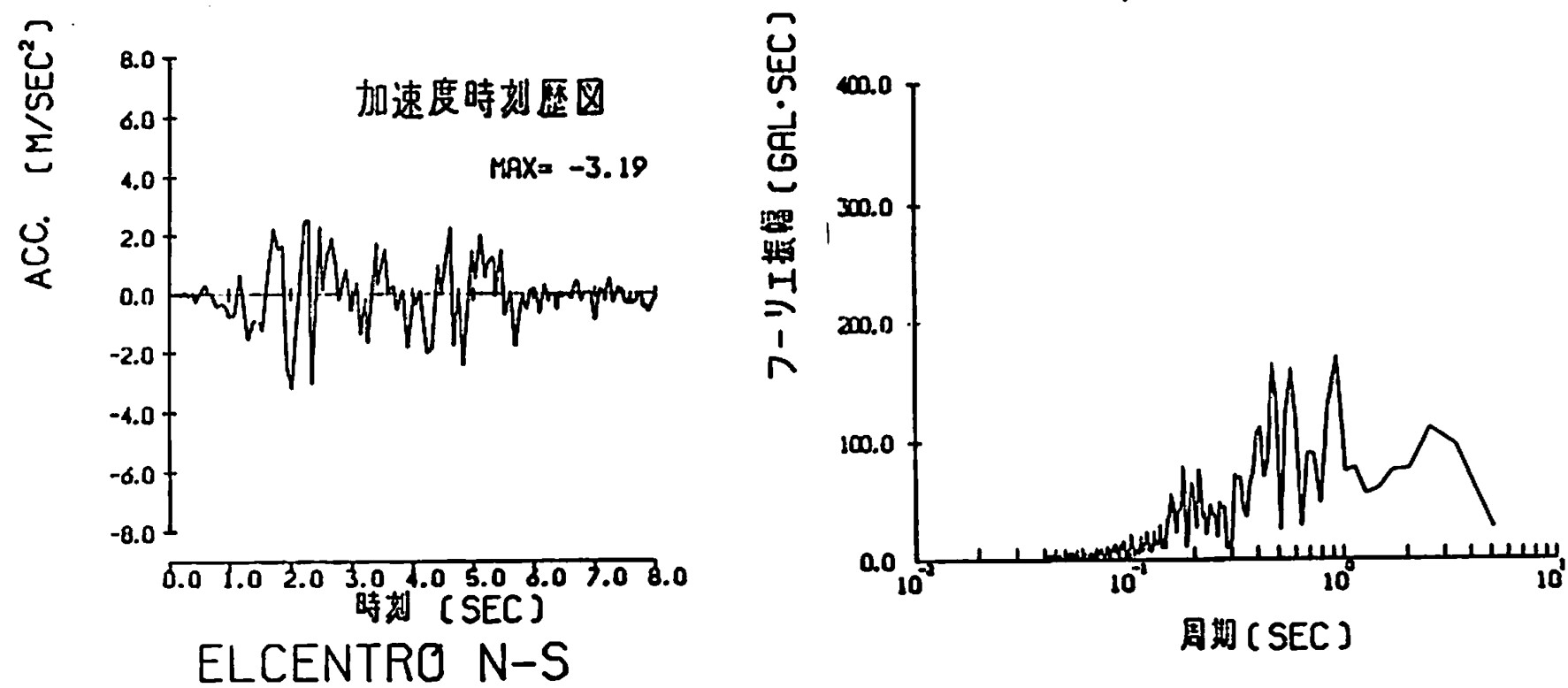
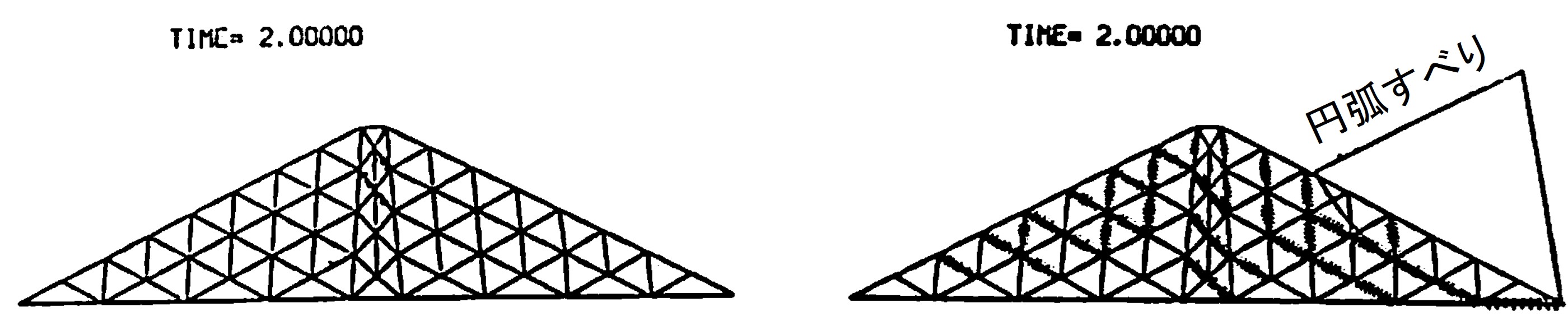
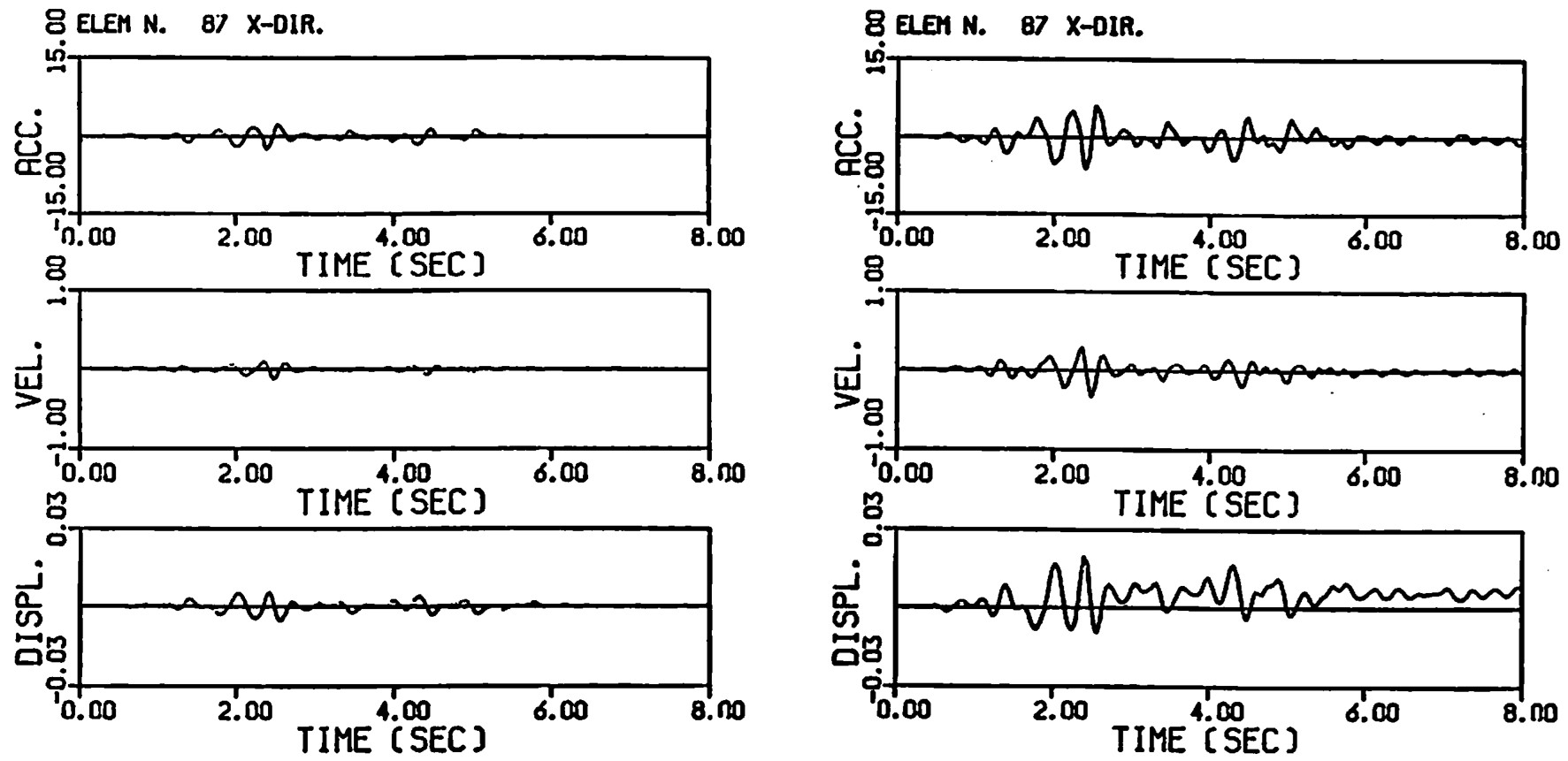
静的結果と動的結果を比較するため静的な弾塑性計算により常時の結果を求め、その値を初期値として弾塑性応答解析を行い地震時の安全率を算出した。また、従来法との比較のため、地震時の円弧すべり解析において水平震度を0.1と0.3とし、これに対応する入力地震波の最大加速度を100galと300galに設定、基盤より水平加振を行った。減衰効果としてレイリー減衰を採用し、係数 $\alpha_0$、$\alpha_1$ の値は1次、2次の減衰定数を $h_1=h_2=0.1$ と仮定して求めた。増分時間は $\Delta t=0.005$秒とし、Newmarkのβ法において $\beta=1/4$ とした。降伏条件にはモール・クーロンの条件を用いている。
以上の前提のもと、
| 材料定数 | 単位 | 値 |
|---|---|---|
| 弾性係数 $E$ | ${\rm tf/m^2}$ | $47100$ |
| ポアソン比 $\nu$ | - | $0.45$ |
| 単位体積重量 $\gamma$ | ${\rm tf/m^3}$ | $2.0$ |
| 粘着力 $C$ | ${\rm tf/m^2}$ | $1.4$ |
| 内部摩擦角 $\phi$ | ${\rm DEG}$ | $37$ |

$\hspace{6em}$
$\hspace{8em}$
$\hspace{6em}$

$\hspace{10em}$
$\hspace{4em}$
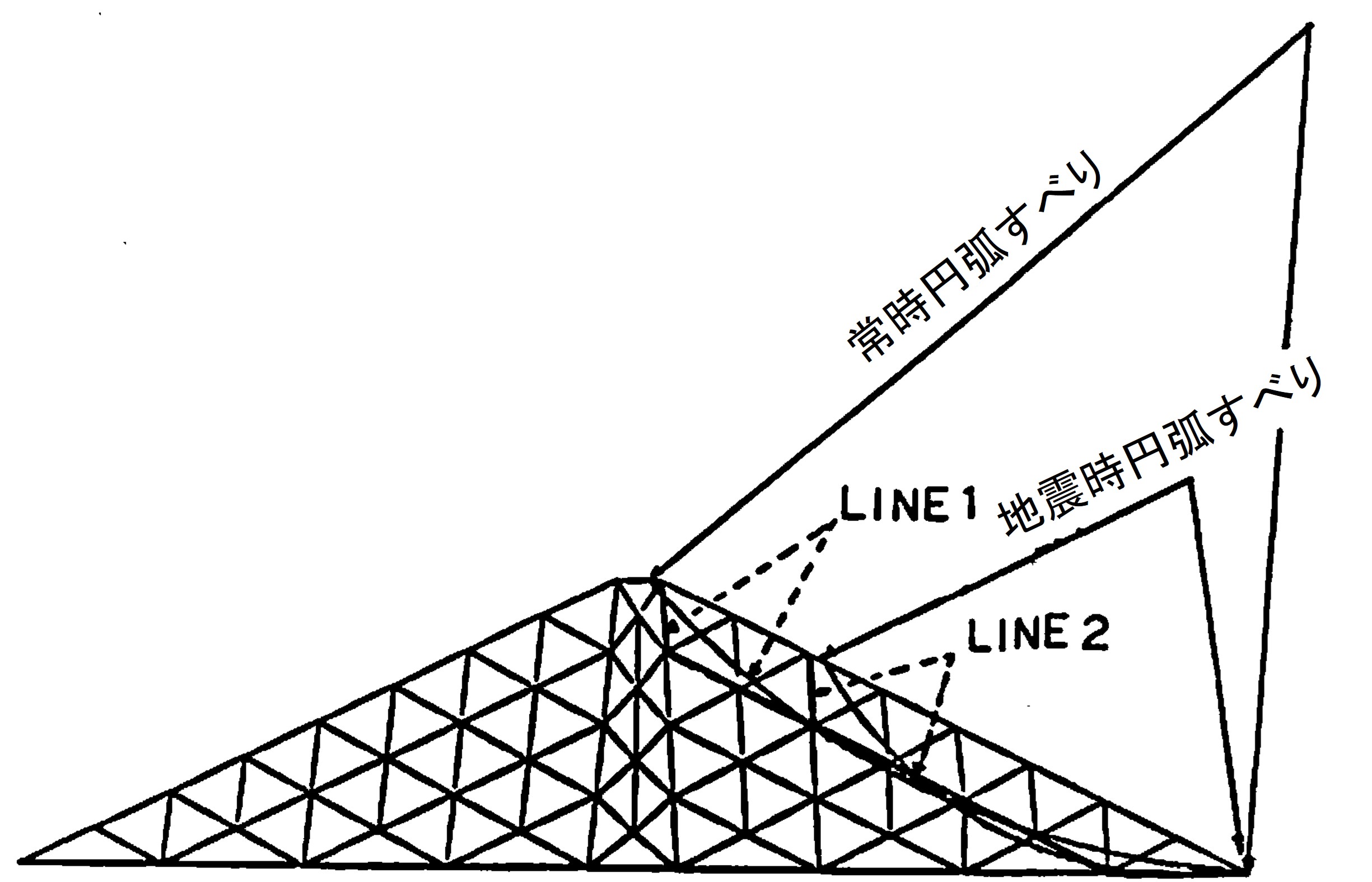
| 解析法 | 常時 | 地震時 | |
|---|---|---|---|
| kh=1.0 | kh=0.3 | ||
| 円弧すべり | 1.79 | 1.47 | 1.03 |
| RBSM | 2.02 | 1.40 | 崩壊 |
7-4 地盤の地震応答解析
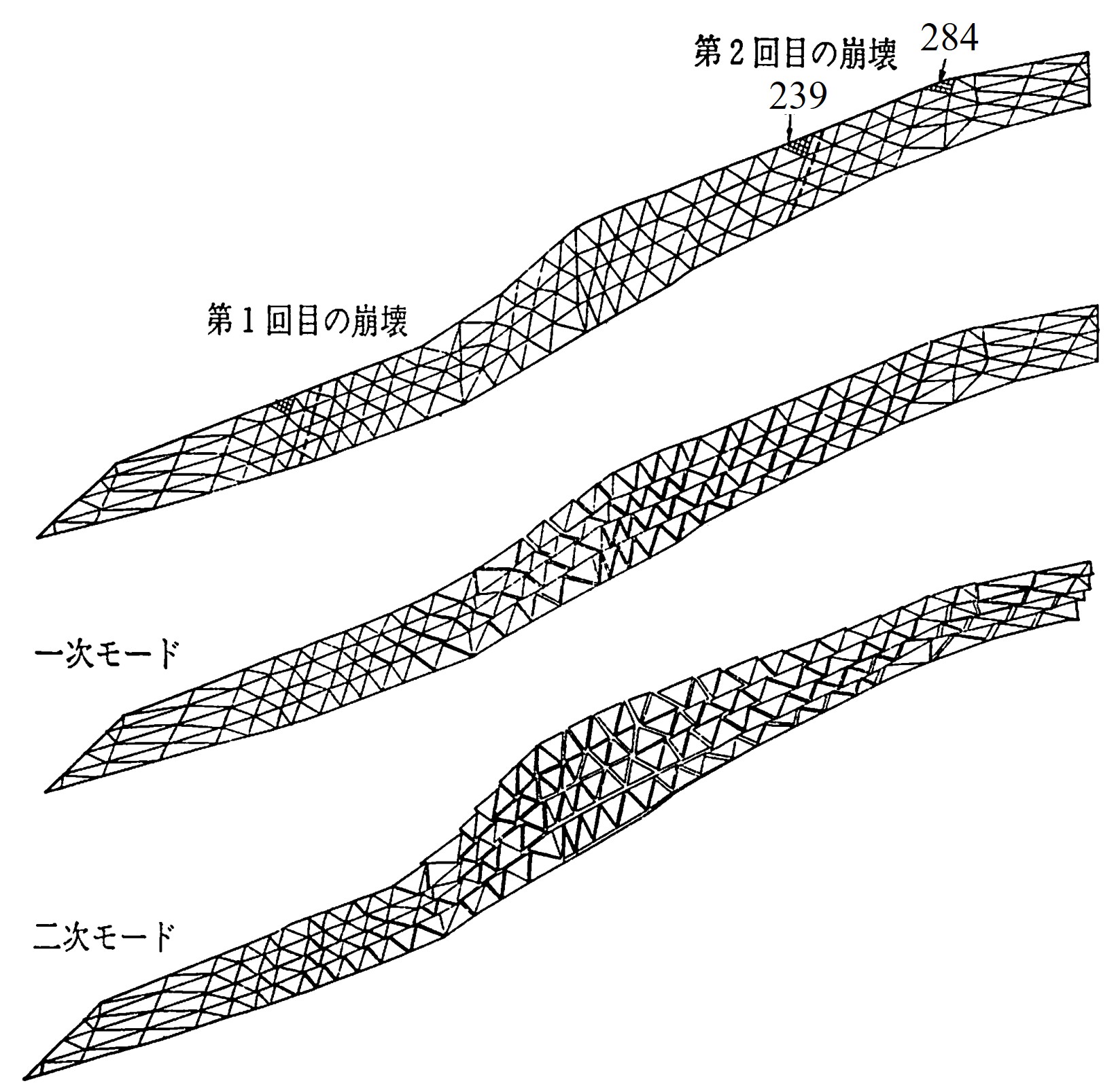
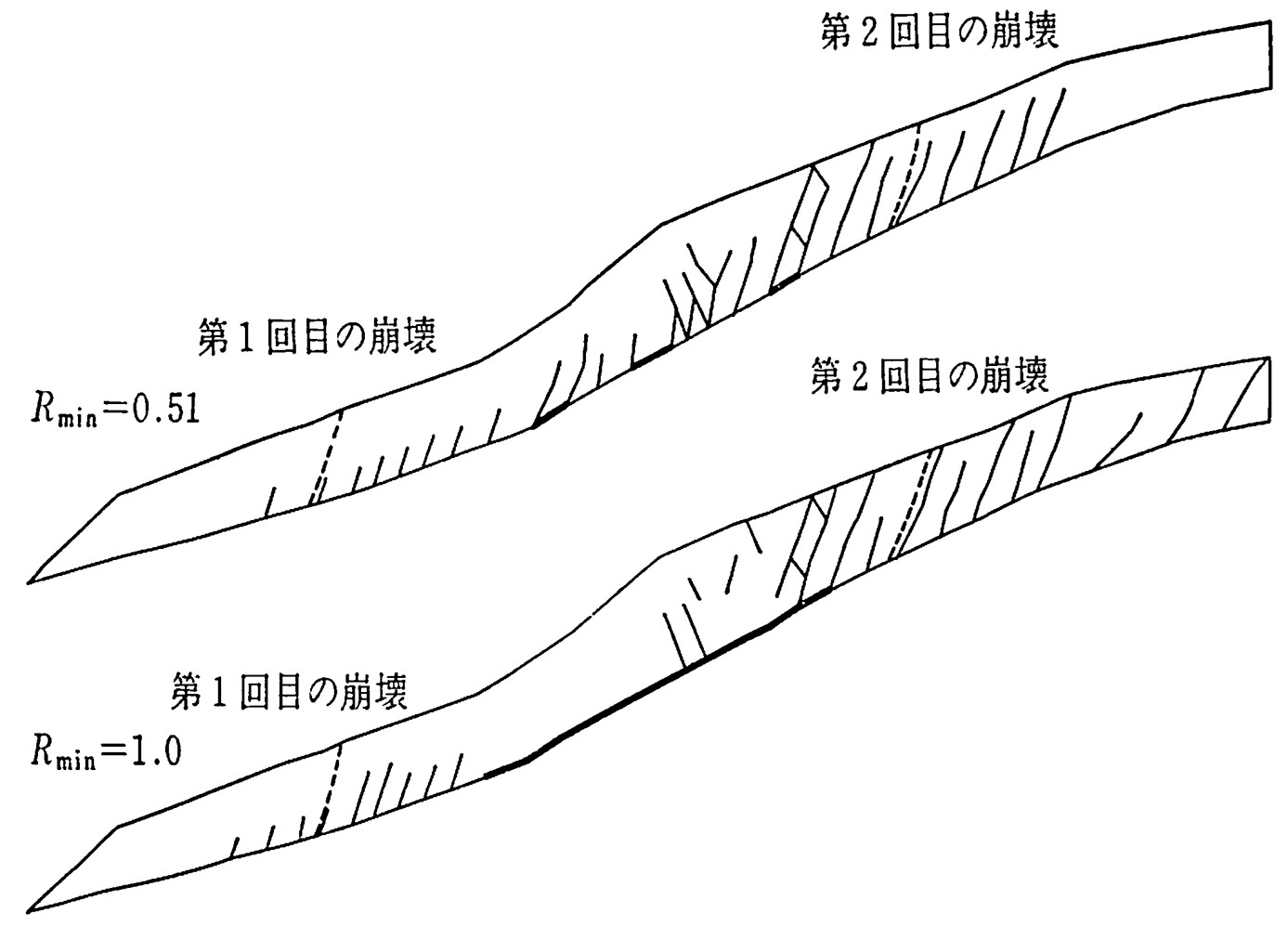
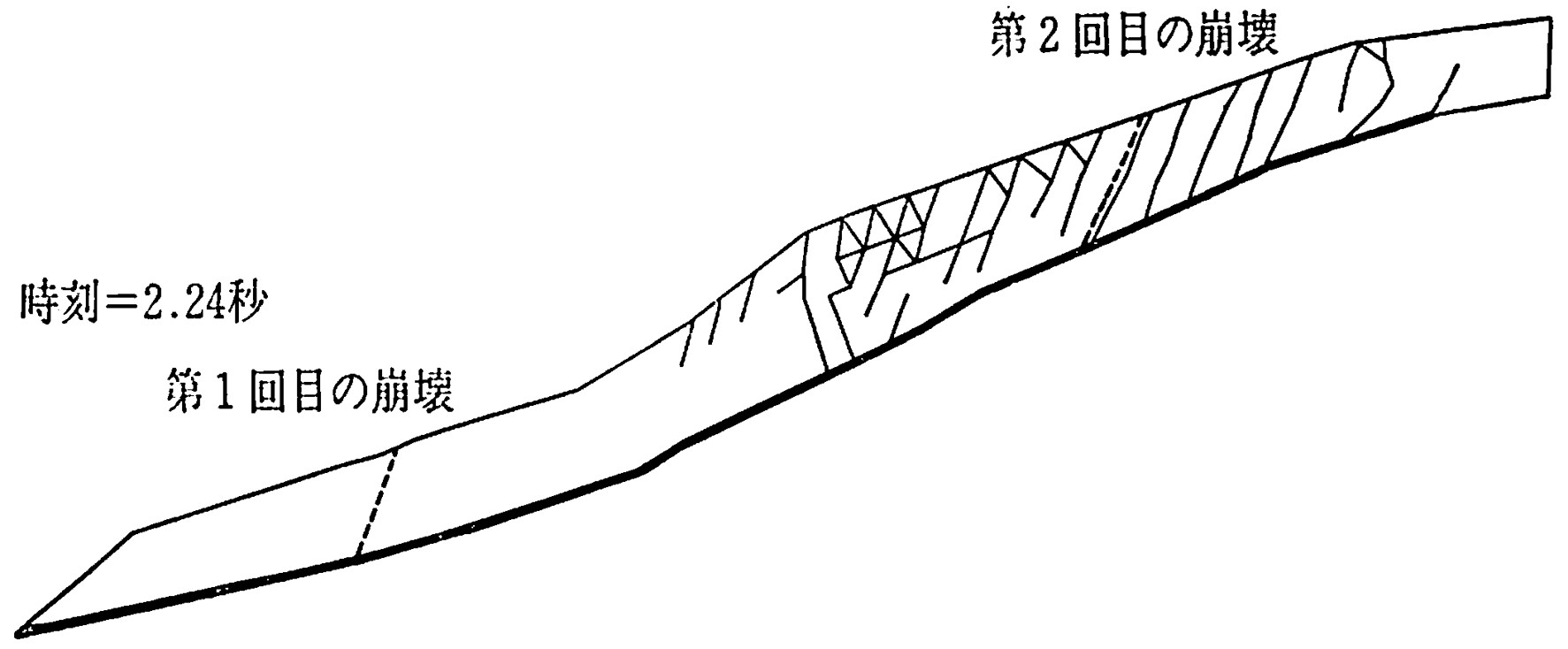
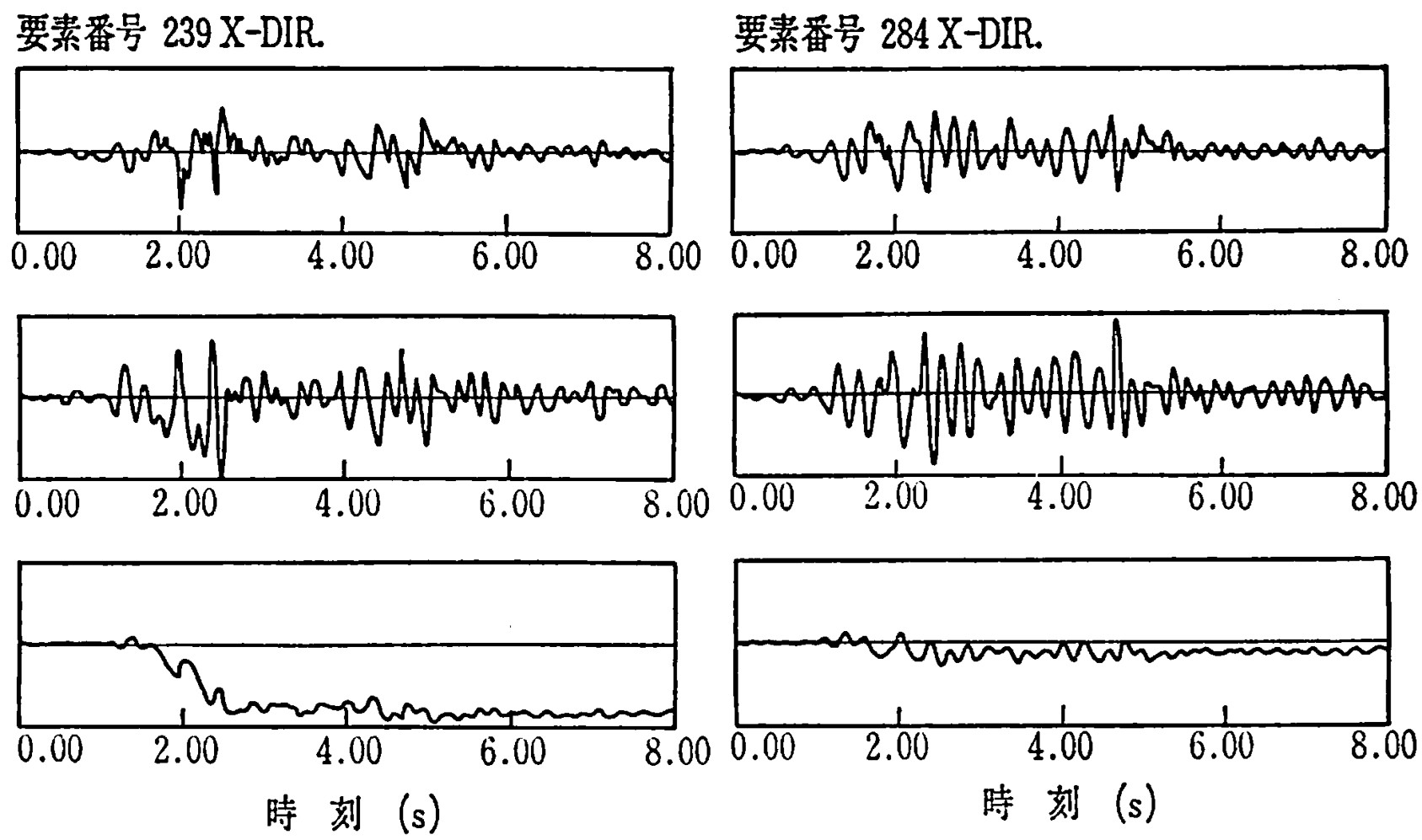
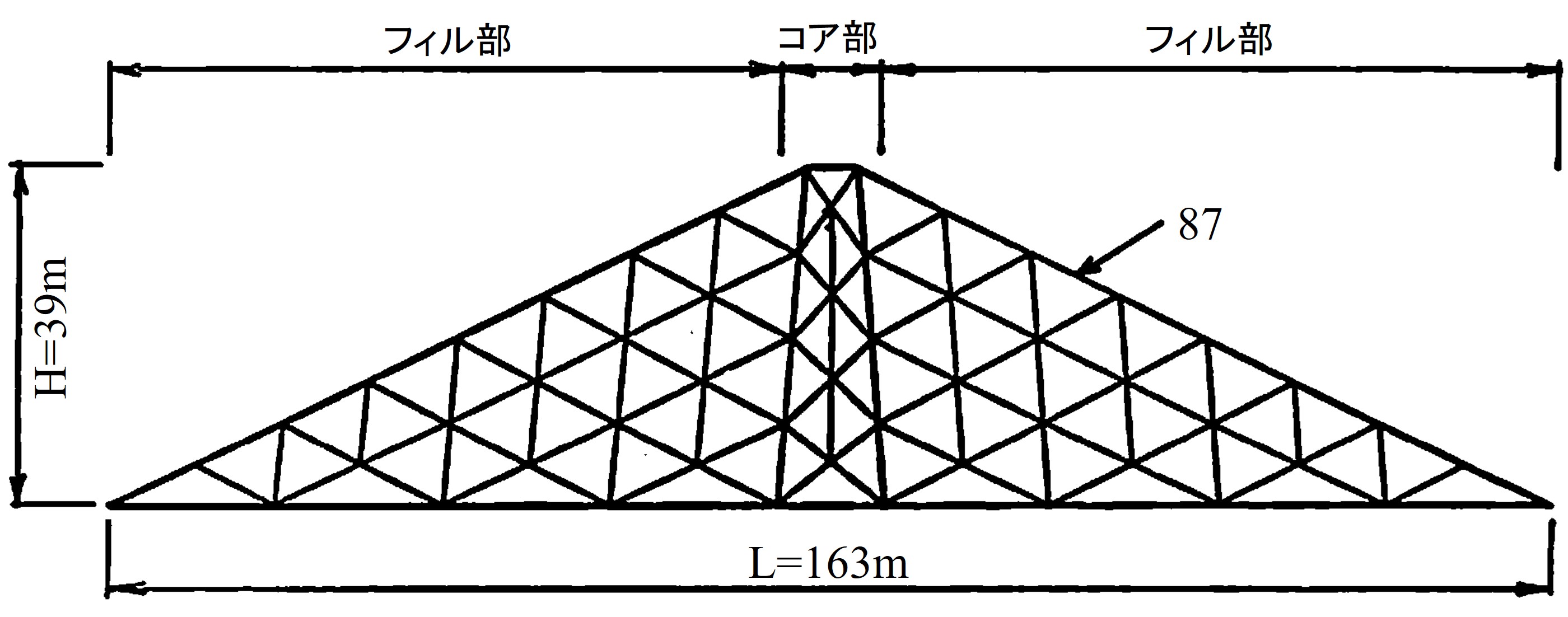
地盤の地震応答解析例として1984年9月に発生した長野県西部地震による御岳大崩壊のシミュレーション結果を紹介しよう。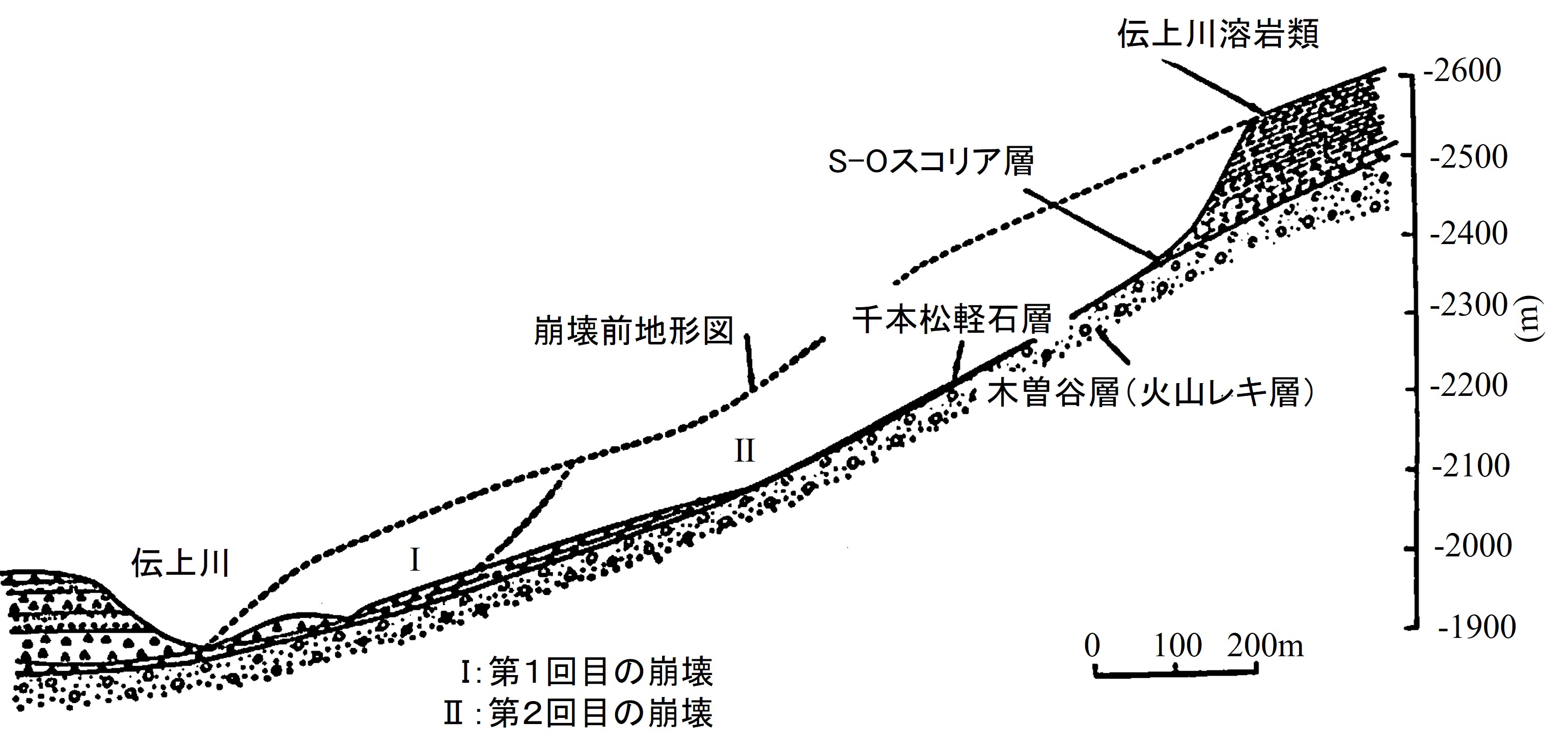
| 材料定数 | 単位 | 値 |
|---|---|---|
| 弾性係数 $E$ | ${\rm tf/m^2}$ | $1.42 \times 10^6$ |
| ポアソン比 $\nu$ | - | $0.25$ |
| 単位体積重量 $\gamma$ | ${\rm tf/m^3}$ | $2.2$ |
| せん断強度 $C$ | ${\rm tf/m^2}$ | $20$ |
| 内部摩擦角 $\phi$ | ${\rm DEG}$ | $35$ |
- 1)地下水の影響を考慮しない千本松軽石層
せん断強さ $C = 15 {\rm tf/m^2}$
内部摩擦角 $\phi = 25^{\circ}$ - 2)地下水の影響を考慮した千本松軽石層
せん断強さ $C = 10 {\rm tf/m^2}$
内部摩擦角 $\phi = 15^{\circ}$
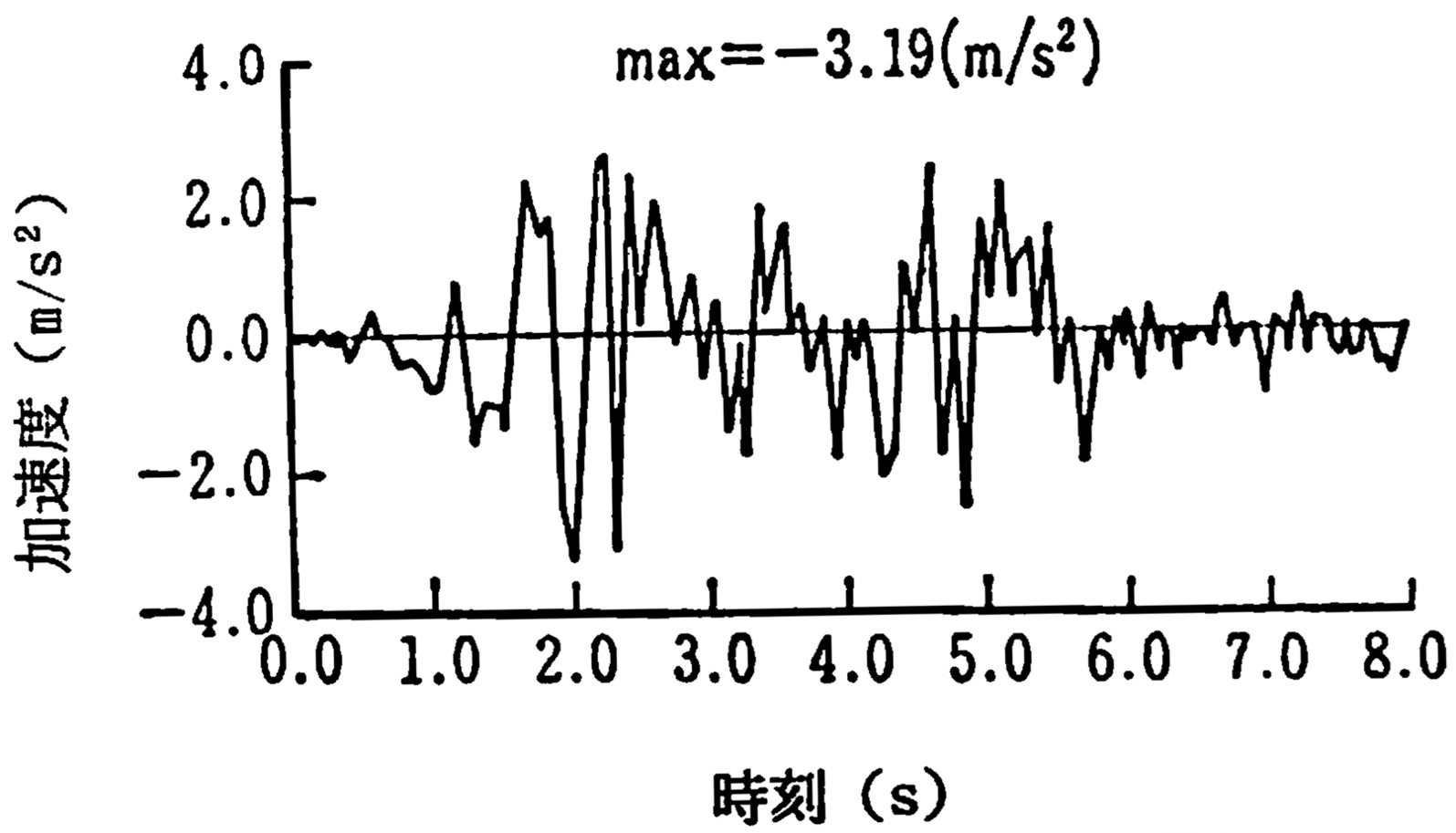
入力地震波については実際の長野県西部地震の波形が得られていないため、マグニチュード6.9 、震源が深さ約3kmであったということより