２．引っ張りに抵抗しない材料の解析法

２－１　はじめに

 一般に、土や岩盤内の節理あるいは断層などは引っ張りに弱く、亀裂が入り易い。したがって、引っ張り応力が生じた部分では、いわゆる「ゆるみ」のような現象が生じていると考えられている。有限要素法では、このようにな問題を解決するため多種多様な解析法が試みられてきた。その中でも、応力遷移法と呼ばれる0.C.Zienkiewicz教授らによって開発された方法は収束性も良く、また、始めに作成された剛性行列を修正せずに計算する方法であるため、演算時間も早い。ただし、クラックが多数発生し、崩壊状態に近づくと一般的に収束性は悪くなる傾向がある。この方法はその呼び名からも理解できるように、与えられた要素分割に対して各要素の材料定数を応力状態に応じて変化させることなく引っ張りに対する余剰力を再配分し収束計算を行う方法であり、本来、不連続体である土や岩盤を連続体として取り扱っている。したがって、当然のことながら、亀裂や断層などの不連続性は考えておらず、実際の土や岩盤などの挙動を的確に表現しえているとは言いがたい。このような欠点を補うため、最近では大きな断層や亀裂などに対し、ジョイント要素などに代表される不連続要素が広く利用されている。
 一方、川井モデルでは分割した各要素を剛体と仮定し、各要素の重心に3つの剛体変位 $(u,v,\theta)$ を自由度として考えているため、各要素境界辺上あるいは多角形（要素）の頂点に自由度を有する節点を持たない。したがって、ついたり離れたりといった、いわゆる接触型の引っ張りクラックを簡単に導入することが可能である。もし、各要素境界辺上に引っ張りクラックが発生したとしても、当初設定した解析上の自由度を変えることなく、始めに作成したパラメーターにより計算することができる。このことは、有限要素法で行われてるような、クラック発生による二重節点化に伴う節点番号の再割付けなどの煩わしい手間が不要であることを示しており、演算時間の短縮化や計算プログラムの簡素化が期待できる。
 川井モデルを用いた引っ張りに抵抗しない材料に対する最も簡単な解析方法は、引っ張り力が生じたバネを切断することであろう。計算上は引っ張りが生じたバネの法線方向および切線方向の両者のバネ係数を0にすれば、この切断を簡単に表現することができる。アルゴリズム的には、一旦、弾性計算を行い引っ張り力が生じたバネを検出し、そのバネが許容値以上の引っ張り力を所有していればバネを切断する。その後始めに戻りばねが切断された状態で再び弾性計算おこなう。これをすべてのばねの引っ張り力が無視できるまで繰り返し計算する。この場合、バネが切断されているため、初めの構造と異なった構造を解析していることになり、いわば、構造異方性として取り扱っていることになる。しかし、このような方法は要素を一つだけ考え、その接触状況を調べるといった特殊な問題の場合を除き、一般的には収束性が悪く、場合によっては異なった破壊パターンを与えかねないため、あまり推奨できない。
 このような問題点は、解放力や一旦発生した引っ張りクラック面の再接触を考慮することにより解決することができる。本章では以上のような引っ張りに抵抗しない材料の解析法として、従来、有限要素法で用いられてきた応力遷移法を川井モデルの立場から説明し、次いで、先に説明したばねを切断するといた川井モデル独特の解析法について述べる。

２－２　応力遷移法

 有限要素法を用いた引っ張りに抵抗しない材料の解析法のうち、主な方法として次ぎの2つが上げられる。その一つは、与えられた構造を弾性体として解析し、その結果得られた応力のうちから引っ張り応力を検出し、その方向の弾性係数を零あるいは極めて小さい値として再度弾性計算を行う方法である。この方法は、材料が引張主応力とその他の方向に対して異方性になるという考え方を基本としており、プログラムが簡単になるなどの幾つかの利点はあるものの引っ張り破壊領域が広い場合には収束性が悪くなり、場合によってはその保証さえ得られないこともある。さらに、初期応力などが存在している場合には解析が困難であるという欠点もあるため、あまり実用的には利用できない。
 もう一つの方法はZienkiewicz教授らが提案した応力遷移法による計算方法で、この方法によれば収束性が保証され、しかも、初期応力が存在していても計算が可能である。ここでは、この応力遷移法を川井モデルに適用する方法について説明する。
 応力遷移法のアルゴリズムは大きく分けて、以下に示すような3段階から構成されている。
 （第1段階）
 （第2段階）
 （第3段階）
 第2段階と第3段階は一見すると複雑なように思えるが、アルゴリズム上は許容値以上の引っ張り力をゼロとし、その応力から計算される等価節点力を逆向きに作用させればよい。このように応力遷移法では弾性計算が基本となっており、矛盾した力を解放することにより正しい応力を求めようとする方法である。したがって、いかに解放すべき拘束力の計算を行うかがボイントになるが、このことについては2.4節で改めて説明する。
 さて、川井モデルでは要素内応力を計算せず、要素境界辺上の表面力を取り扱っているため、有限要素法と取り扱う物理量が異なる。そのため、先の説明では応力の代わりに単位面積当たりの表面力という言葉を使ったが、基本的なアルゴリズムは有限要素法による応力遷移法の説明と全く同じであることに気付かれたであろう。FEMの応力をRBSMの表面力に置き直して考えればRBSMの計算の流れは、ほぼ有限要素法と同様になる。図2.1は応力遷移法による解析の流れを川井モデル用に書き直したものであるが、剛性行列の内容や取り扱う物理量の表現など、細かい点では有限要素法と当然異なっている。しかし、少なくともこの流れを見る限りにおいては両者に大差はない。
 
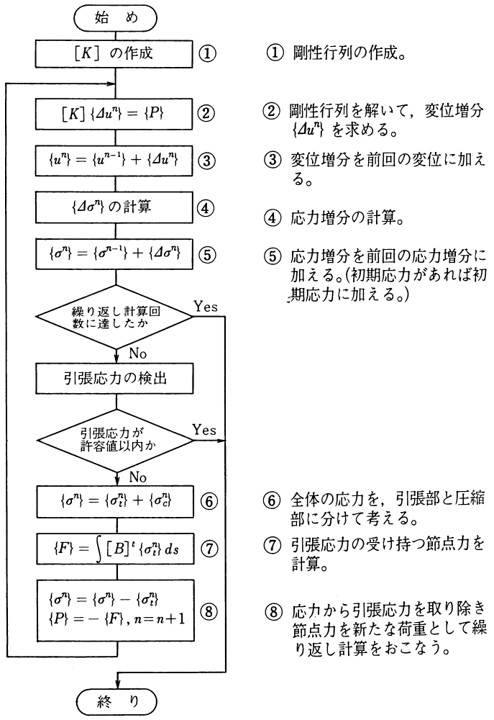
$\hspace{6em}$図2.1　応力遷移法のアルゴリズム
 本手法の欠点は、不連続面を連続体近似で表現していることである。すなわち、引っ張り力に伴うクラックの導入を行わず、見かけの応力でのみ処理することにある。したがって｀得られた変位の信頼性は必ずしも高いとはいえない。このような応力遷移法を川井モデルに適用した場合、得られる解の特性は有限要素法と同様な性質を持っており、したがって、不連続面を連続体近似していることに変わりはない。有限要素法の場合、連続体近似を前提としているため、このような解析方法が考えられたのであろうが、川井モデルはすべりやクラックなどの不連続性を表現すのに適したモデルであり、このような手法を適用することは、解析すべき問題にもよるが、初期応力の計算以外あまり得策でないケースの方が多いようである。
ばんｒ」

２－３　TENSION-CRACK解析法

 川井モデルでは要素重心に自由度を設定し、その自由度を利用して要素境界辺上の相対変位から「ばね」という概念を通して表面力を求めている。前節の初めに引っ張り力が生じている方向の弾性係数を零とする方法を述べたが、これを川井モデル的に考えると、その方向の「ばね」を切断するということと等価になる。この方法はプログラミングが簡単であり、また、接触問題などへの応用が可能であるなど、多くの利点を持っているが、その反面収束性の保証がなく、しかも、初期応力の存在する問題が扱いにくいなど、地盤の応力解析にとって致命的な欠点も多く、あまり実用的には利用できない。
 また、前節で述べた解析法もクラックが発生したときの挙動に関しては信頼性が乏しく、連続体仮説の域を脱しえない。特に、粒状体の集合のような不連続体をこの方法により解析した場合、実際と異なった挙動を示すこともある。一方、川井モデルでは重心の剛体変位 $(u,v,\theta)$ をパラメーターとするため、有限要素法のように節点変位が連続であるといった拘束条件が付いていない。したがって、許容値以上の引張力が要素境界辺上に生じた場合、その境界辺を伝達している力を断ち切ったり、逆に、一旦、引張破壊して力の伝達が絶たれている境界辺に対し、再び接触し力を伝えるよう考慮することは何等困難なことではない。しかも、二重節点のように、初めに設定した自由度が増加するといった心配もない。このような観点から開発されたのが、本節で説明するTENSION-CRACK解析法である。
 図2.2はTENSION-CRACK解析法の計算の流れを示したもので、計算アルゴリズムは次ぎの4段階から構成されている
 
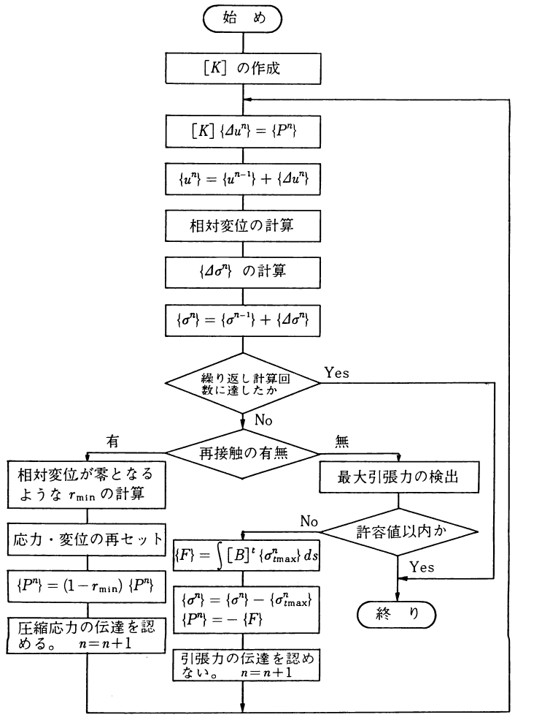
$\hspace{4em}$図2.2　TENSION-CRACK解析法のアルゴリズム
 （第1段階）
 （第2段階）
 （第3段階）
 （第4段階）
 以上示したように本アルゴリズムは解放力を与えながら増分計算を行ってゆく方法である。本手法におけるポイントは再接触を認めている点にある。これは弾塑性解析でいうところの除荷、負荷過程のようなプロセスと考えることができ、収束性や得られる解の信頼性を増している。解放力の考え方については先の応力遷移法と同様であり、2.4節で改めて説明する。
 本手法を用いることで、引っ張りクラックの導入、接触問題の解析、弾塑性解析との組合せなどの広範囲にわたる分野の解析が可能となり、川井モデルの応用性が広るものと思われる。

２－４　解放力の計算方法

 応力還移法による解析法やTension-Crack解析法では許容値以上の引っ張り力が生じた場合、その引っ張り力と等価でしかも符号が逆向きの力を加えることによってそのバネが所有していた力を解放する。ここでは、この解放力をどのように計算するか、その求め方について説明する。
 川井モデルでは要素境界辺上に設定したバネを通して力が伝わると考えている。したがって、隣接する2要素間には図2.3に示すような向きを正とする表面力が作用していることになる。ここで、 $(T_n,T_s)$ は単位面積当りの表面力である。
 
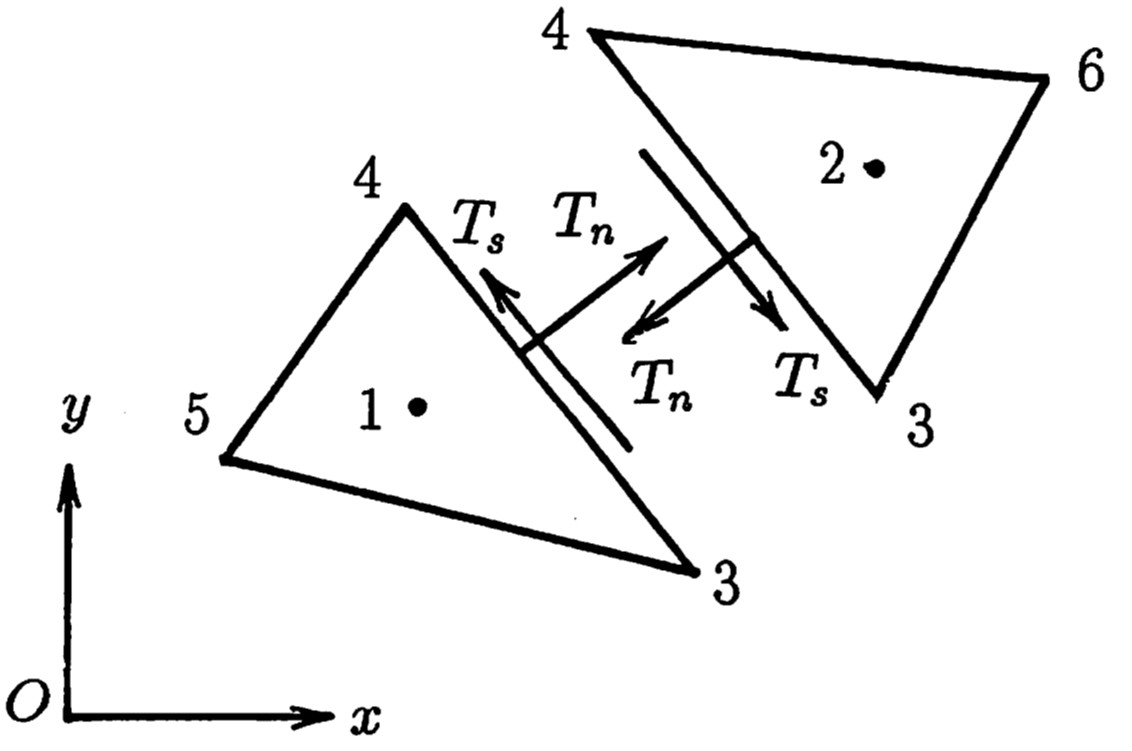
$\hspace{4em}$図2.3　川井モデルの表面力
 ここで、要素境界辺の長さを $L$ とし各節点の座標を $x_i$、$y_i$とすれば、それぞれの表面力は図2.4を参照し以下のような関係にあることが理解できる。
 
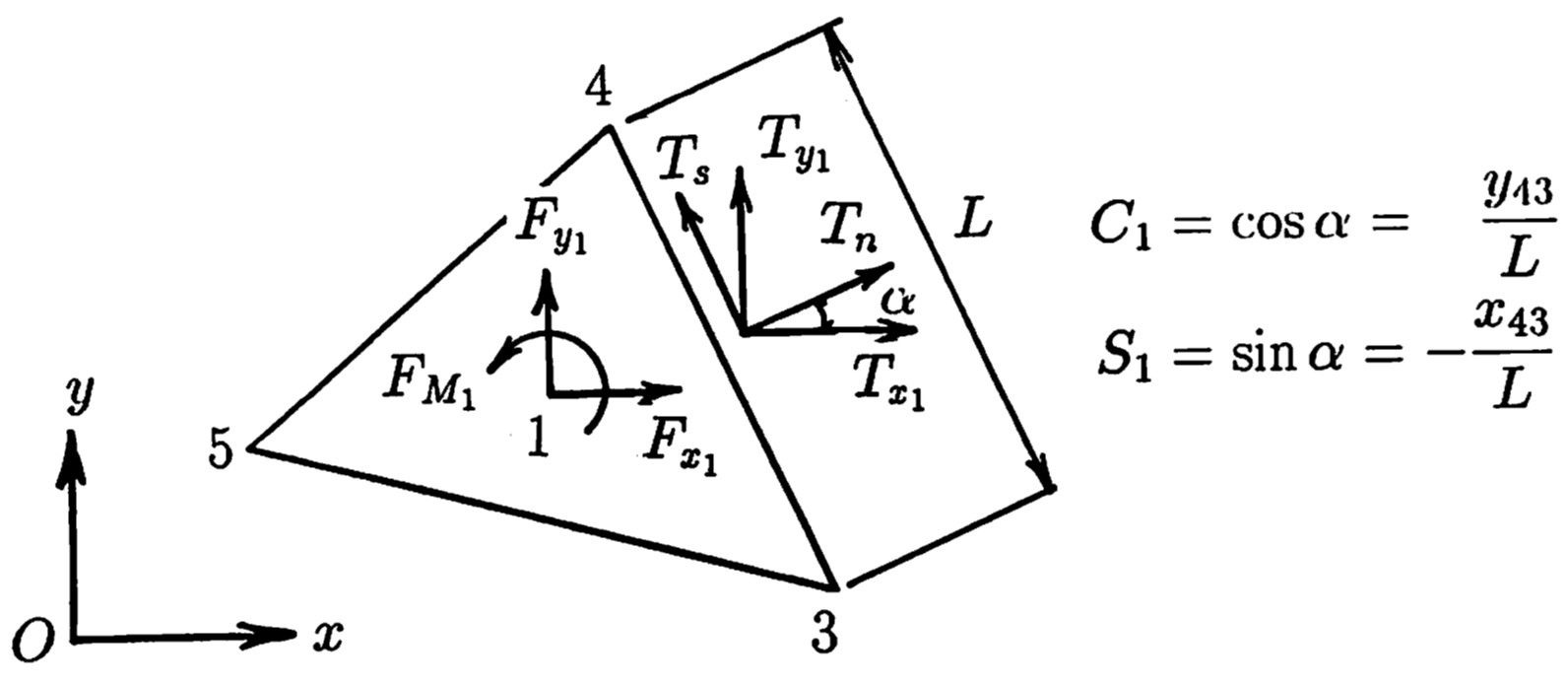
$\hspace{4em}$図2.4　要素①の表面力と節点力
\[{\rm (2.1.a)}   \left\{ \begin{array}{l} T_{n} \\ T_{s} \end{array} \right\} = \left[ \begin{array}{rr} C_{1} & S_{1} \\ -S_{1} & C_{1} \end{array} \right] \left\{ \begin{array}{l} T_{x_{1}} \\ T_{y_{1}} \end{array} \right\} \] \[{\rm (2.1.b)}   \left\{ \begin{array}{l} T_{x_{1}} \\ T_{y_{1}} \end{array} \right\} = \left[ \begin{array}{rr} C_{1} & -S_{1} \\ S_{1} & C_{1} \end{array} \right] \left\{ \begin{array}{l} T_{n} \\ T_{s} \end{array} \right\} \]
 一方、境界面上に働く表面力の重心に関する合力 $(df_{x_1},df_{y_1},df_{M_1})$ は同様に図2.4を参照し、以下のように計算することができる。
\[{\rm (2.2)}   \left\{ \begin{array}{l} df_{x_{1}} \\ df_{y_{1}} \\ df_{M_{1}} \end{array} \right\} = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ -(y-y_{1}) & (x-x_{1}) \end{array} \right] \left\{ \begin{array}{l} T_{x_{1}} \\ T_{y_{1}} \end{array} \right\} \]
ここで、$d \boldsymbol{f}$ は単位面積当りの表面力が作用したために生じる重心における合カであることを示している。したがって、式(2.2) に式(2.1) を代入することにより以下の関係が得られる。
\[{\rm (2.3)}   \left\{ \begin{array}{l} df_{x_{1}} \\ df_{y_{1}} \\ df_{M_{1}} \end{array} \right\} = \left[ \begin{array}{cc} C_{1} & -S_{1} \\ S_{1} & \;\;\; C_{1} \\ -C_{1}(y-y_{1})+S_{1}(x-x_{1}) & S_{1}(y-y_{1})+C_{1}(x-x_{1}) \end{array} \right] \left\{ \begin{array}{l} T_{n} \\ T_{s} \end{array} \right\} \]
 一方、要素②についても同様に考えることができる。いま、図2.5に示すように座標軸の回転を $\alpha$ とする。このとき、$\alpha$ は要素①の $\alpha$ と同じ値となる。
 
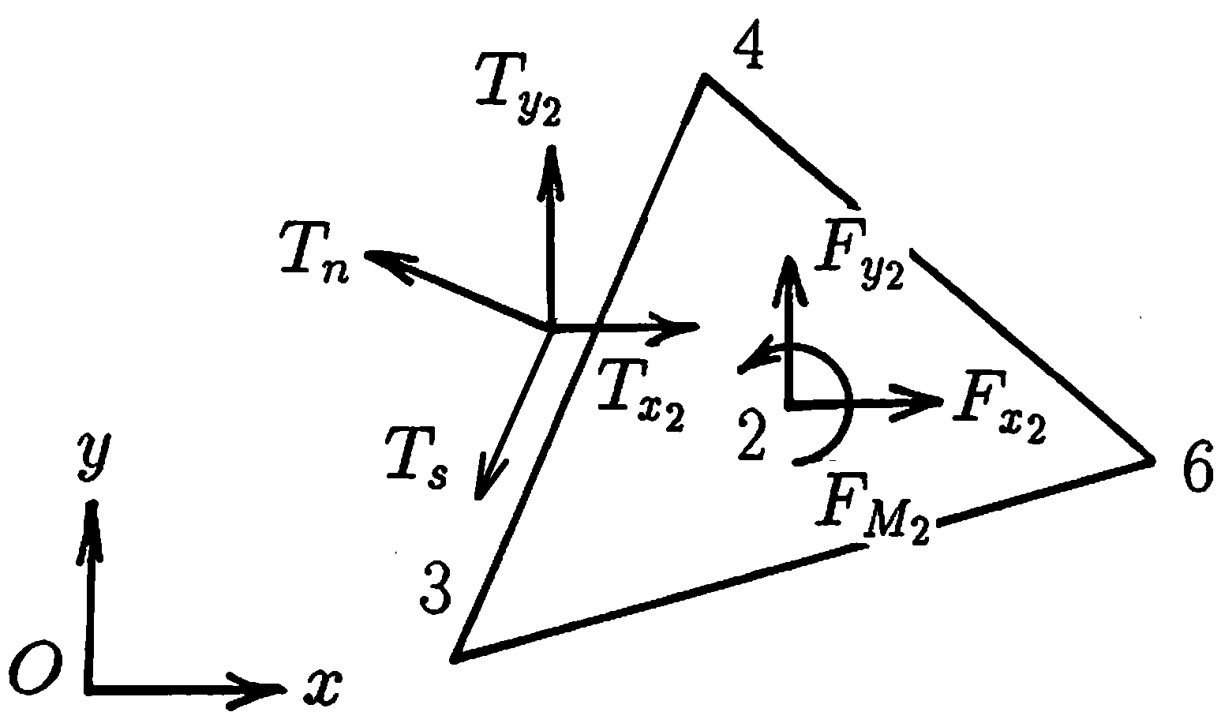
$\hspace{2em}$図2.5　要素②の表面力と節点力
 ところが、幾何学的にも理解されるように要素②における全体座標系と局所座標系の間には $\alpha + 180^{\circ}$ の回転が考えられるから、結局、方向余弦は以下のようになる。
\[{\rm (2.4)}   \left. \begin{array}{lcll} C_{2} & = & \cos \; ( \alpha +180 ) & = -C_{1} \\ S_{2} & = & \sin \; ( \alpha +180 ) & = -S_{1} \end{array} \right\} \]
 したがって、要素①の場合とまったく同様な手順を踏み、要素②の重心に関する合力が式(2.5)のように求められる。
\[{\rm (2.5)}   \left\{ \begin{array}{l} df_{x_{2}} \\ df_{y_{2}} \\ df_{M_{2}} \end{array} \right\} = \left[ \begin{array}{cc} C_{2} & -S_{2} \\ S_{2} & \;\;\; C_{2} \\ -C_{2}(y-y_{2})+S_{2}(x-x_{2}) & S_{2}(y-y_{2})+C_{2}(x-x_{2}) \end{array} \right] \left\{ \begin{array}{l} T_{n} \\ T_{s} \end{array} \right\} \]
 以上のようにして得られた合力 $d \boldsymbol{f}$ は単位面積当りの表面力に関する力であるため、各要素境界辺に沿った線積分を以下のように行うことにより、最終的に全表面力による解放力 $\boldsymbol{F}$ を式(2. 6)のように計算することができる。
\[{\rm (2.6)}   \boldsymbol{F} = -\int_{l_{35}} (d \boldsymbol{f} )ds \]
 なお、この式(2.6)における係数行列は面内変形平板要素において、要素剛性行列や応力を求める場合に利用する $\boldsymbol{B}$ マトリックスの逆符号と一致している。

２－５　数値計算例

 はじめに、本章で説明したアルゴリズムに対する妥当性ならびに収束性を数値実験の立場から証明する。図2.6には解析に用いたモデルと要素分割が示してある。この例題は引っ張りに抵抗しない材料が上下端で鉛直方向に拘束され、図のような分布荷重を受けた状態を想定している。ただし、自重は無視している。
 
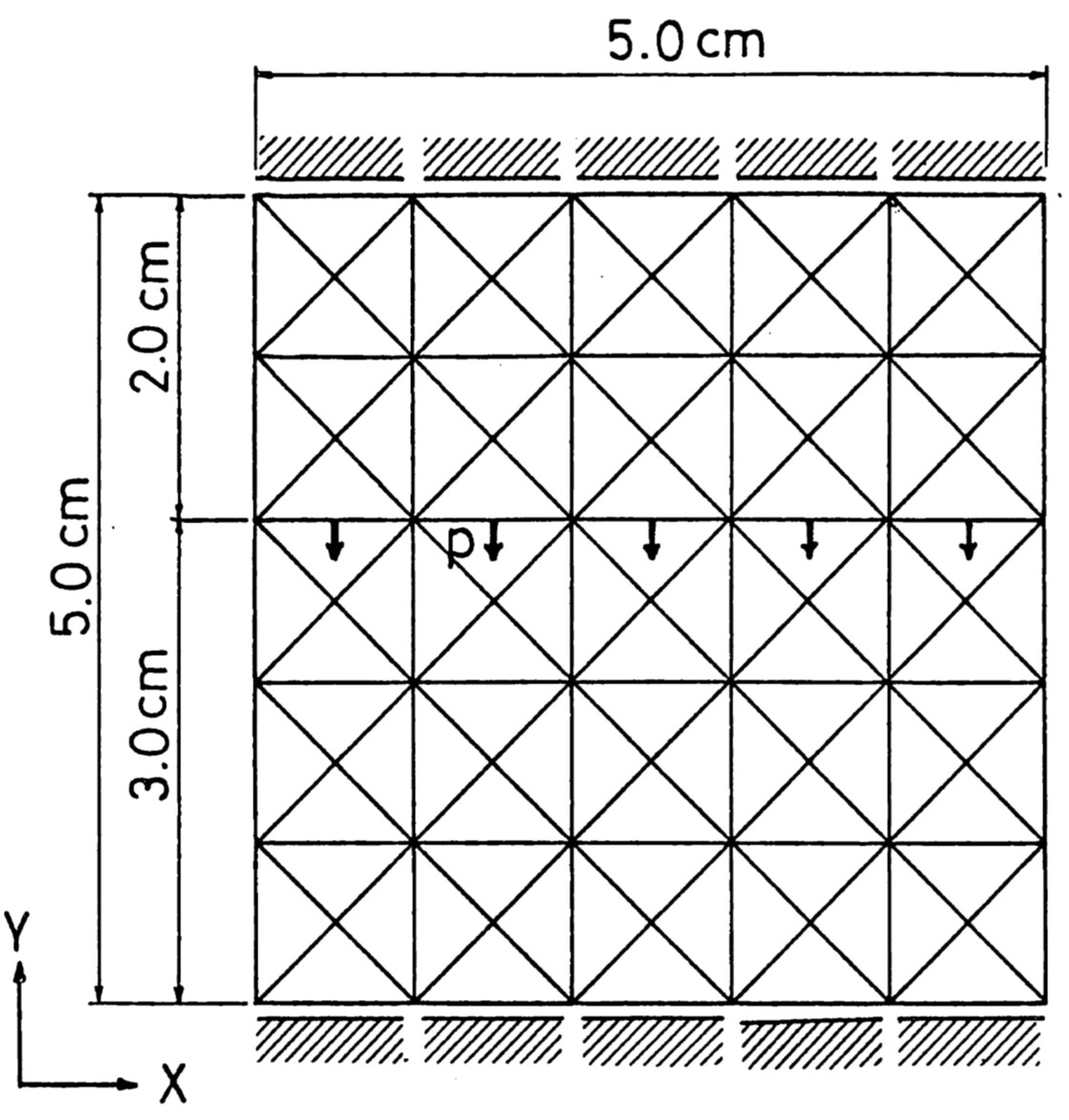
$\hspace{0em} p = 1 {\rm kgf/cm^2} \;\; E = 1.0 {\rm kgf/cm^2} \;\; \nu = 0.3$
$\hspace{2em}$図2.6　計算モデルと材料定数
 弾性計算では載荷面より上側の部分に引っ張り力が生ずる。一方、無引張解析では許容引張力を0としているため、収束計算後には図2.6下側ですべての荷重を受け持つことになる。
 図2.7は2.2節で説明した応力遷移法による収束状況を示した図である。
 
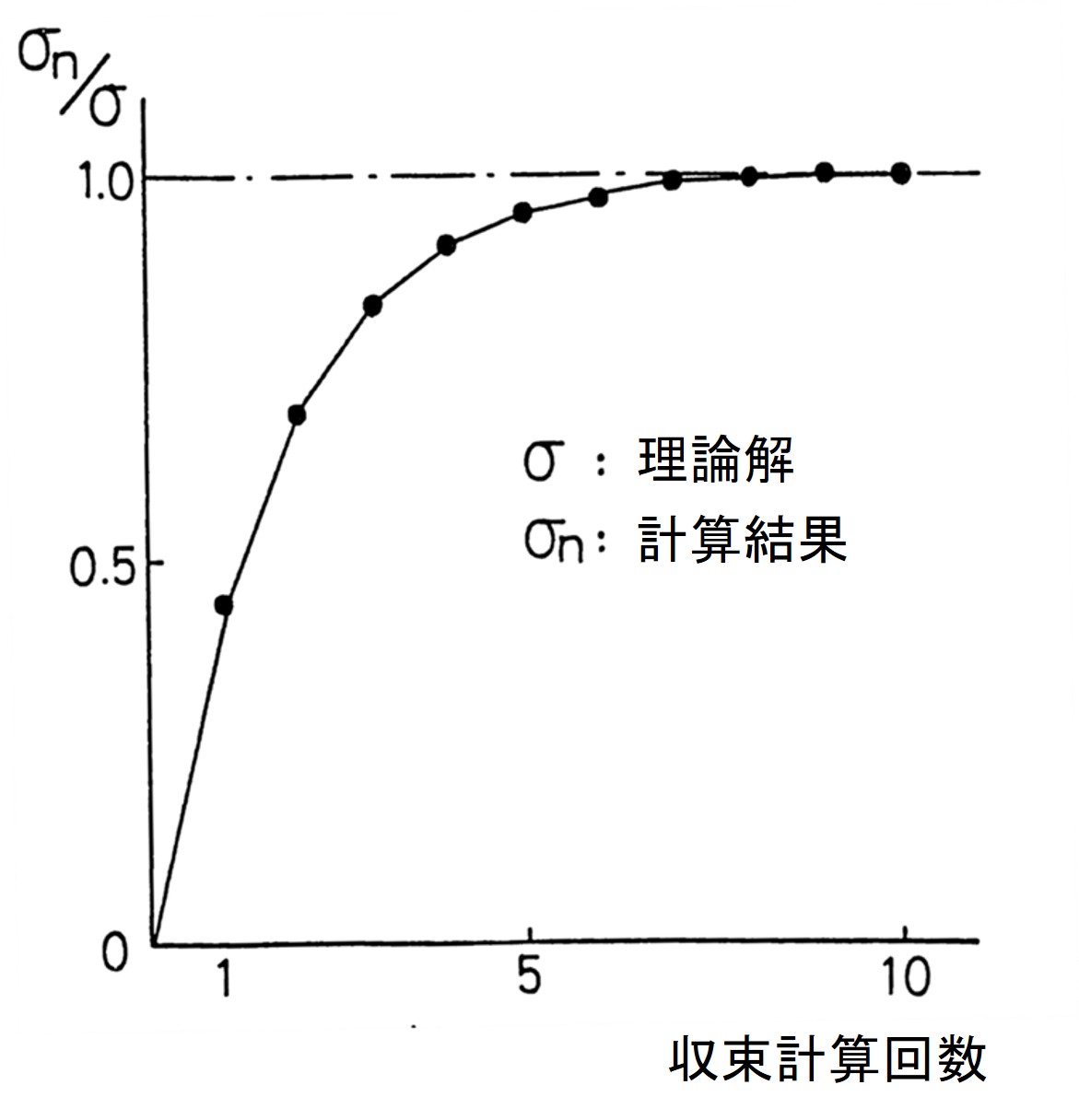
$\hspace{0em}$図2.7　No-TENSION法における収束状況
図の縦軸は載荷面より下側の応力を理論解で無次元化した値であり、横軸は収束計算回数を示している。応力遷移法による解析の場合、載荷面より上側の応力が完全に0となることはないため、収束判定基準を0とすると、ほとんど無限に計算を繰り返してしまう。そこで、本例題では十分小さな値として許容張応力を $0.005 {\rm kgf/cm^2}$ と考えた。この結果、17回の繰り返し計算で収束した。しかし、図からも理解できるように、実用的には1 0回程度の繰り返し計算で十分満足のゆく結果が得られている。このように、応力遷移法を利用する場合はどのような収束判定基準を設定するかで計算効率に差が生ずる。
 一方、図2.8はTENBSION-CRACK法と応力遷移法による変形パターン、繰り返し計算回数、ならびに演算時間を比較した図である。
 
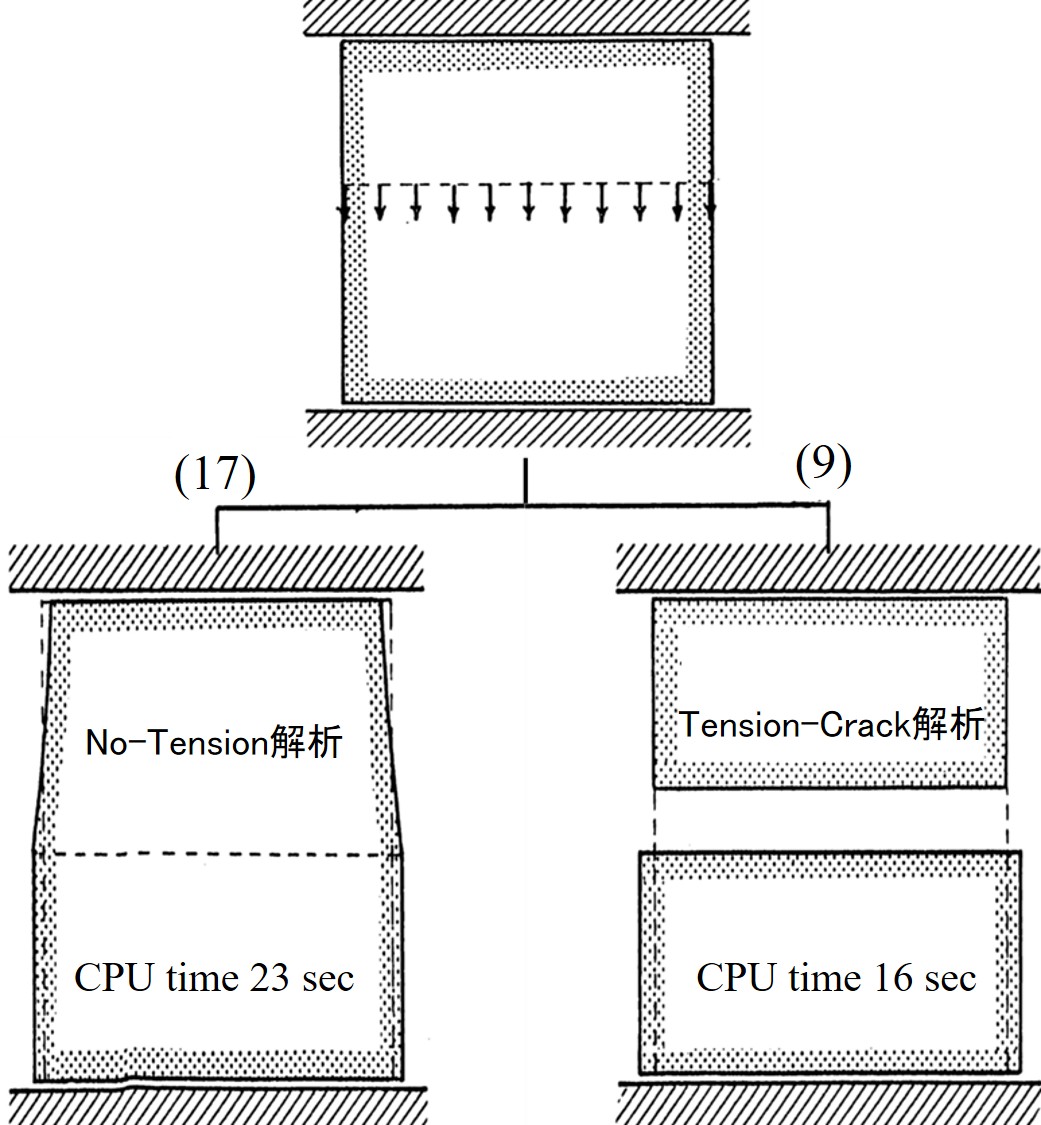
$\hspace{4em}$図2.8　変形モード
両者の解析法における応力の値はほぼ同程度となっているが、変形モードは大きく異なる。板の上に置かれた砂のような物を想像すればわかると思うが、通常、応力遷移法のような変形モードではなく、TENSION-CRACK法のような変形モードが発生する。計算時間についても両者の間には大差がなく、川井モデルを利用する湯合は、問題の種類にもよるが、TENSION-CRACK法的扱いの方が適していよう。
 図2.9は斜面上に設置された杭の模型実験に対するシミュレーションモデルである。この実験では、基礎地盤としてセッコウとケイソウ土を混ぜたものを使用しており、杭としては $\phi 34$ の鉄筋を用いている。また、杭に水平荷重を作用させたとき模型が前方へ転倒しないよう、左上部に浮き上がり防止を行っている。そこで、数値実験を行うにあたり、この部分の鉛直方向変位を拘束した。
 
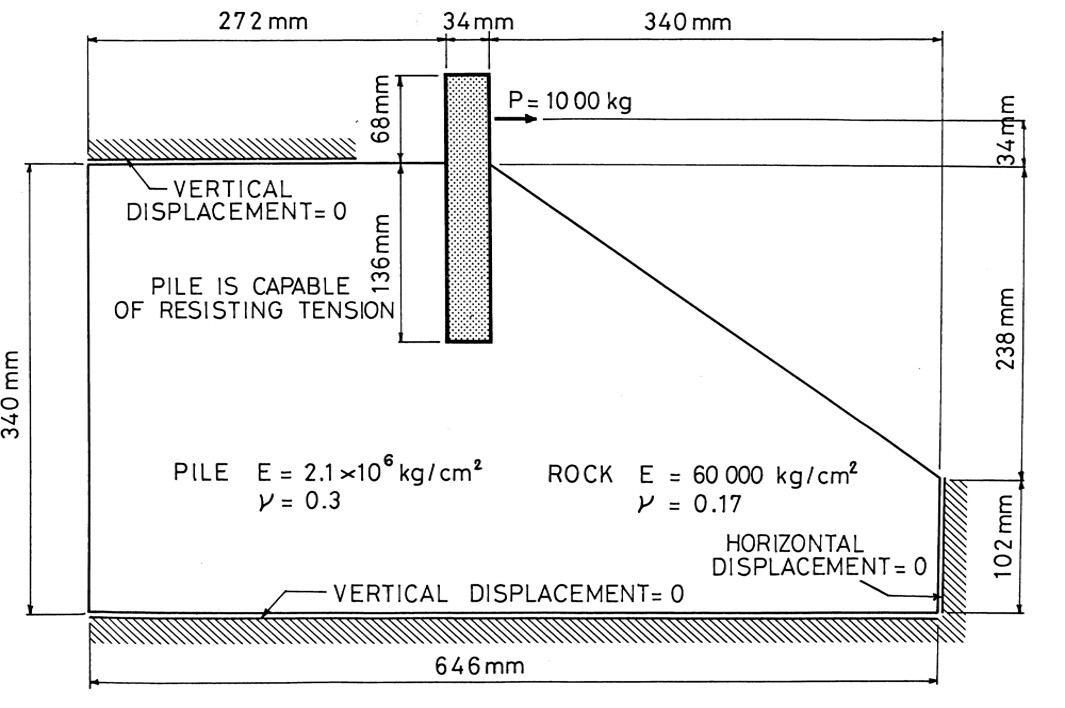
$\hspace{6em}$図2.9　斜面上の杭の計算
 図2.10は解析に用いた要素分割が示されている。拘束を含む全自由度数は528である。図2.11 は応力遷移法による解析結果で、杭前方に引っ張り領域が移動してゆく様子が現れている。しかし、この解析法では明確な破壊線が現れていない。
 
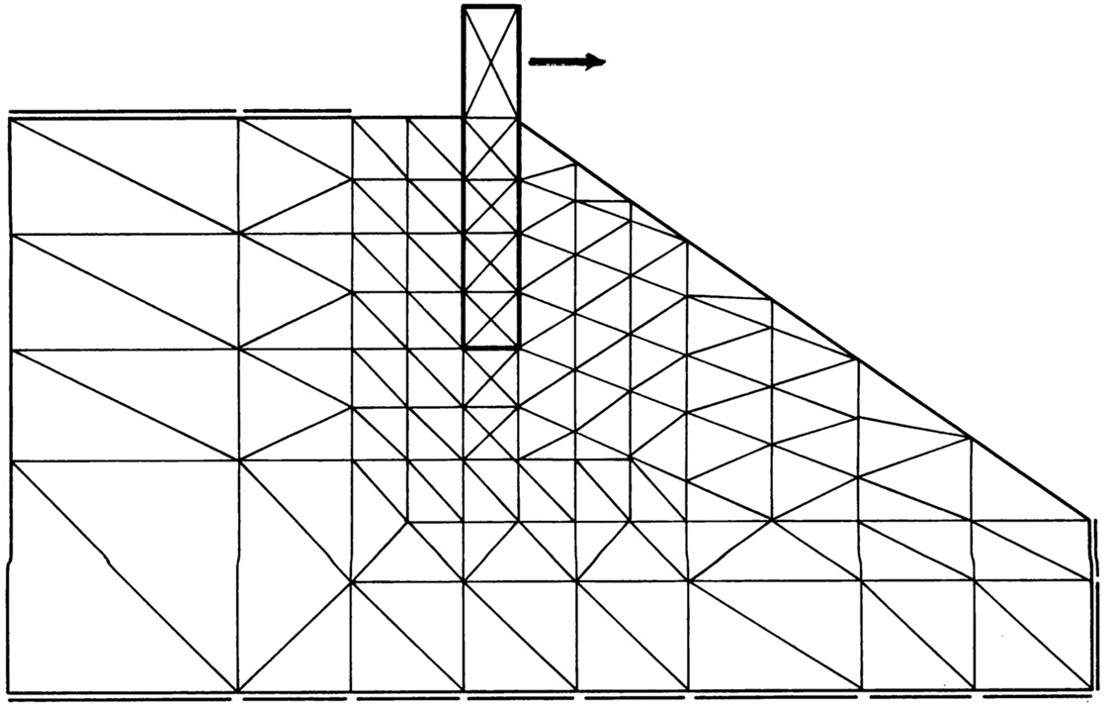
$\hspace{6em}$図2.10　要素分割図
 一方、図2.12はTENSION-CRACK法による結果で、実線により示されている部分が引っ張り破壊の生じている位置であり、網掛けの部分は若干残っている許容値以下の引っ張り領域を表している。本例では、14ステップ目で崩壊機構を形成し、計算が発散する。
 
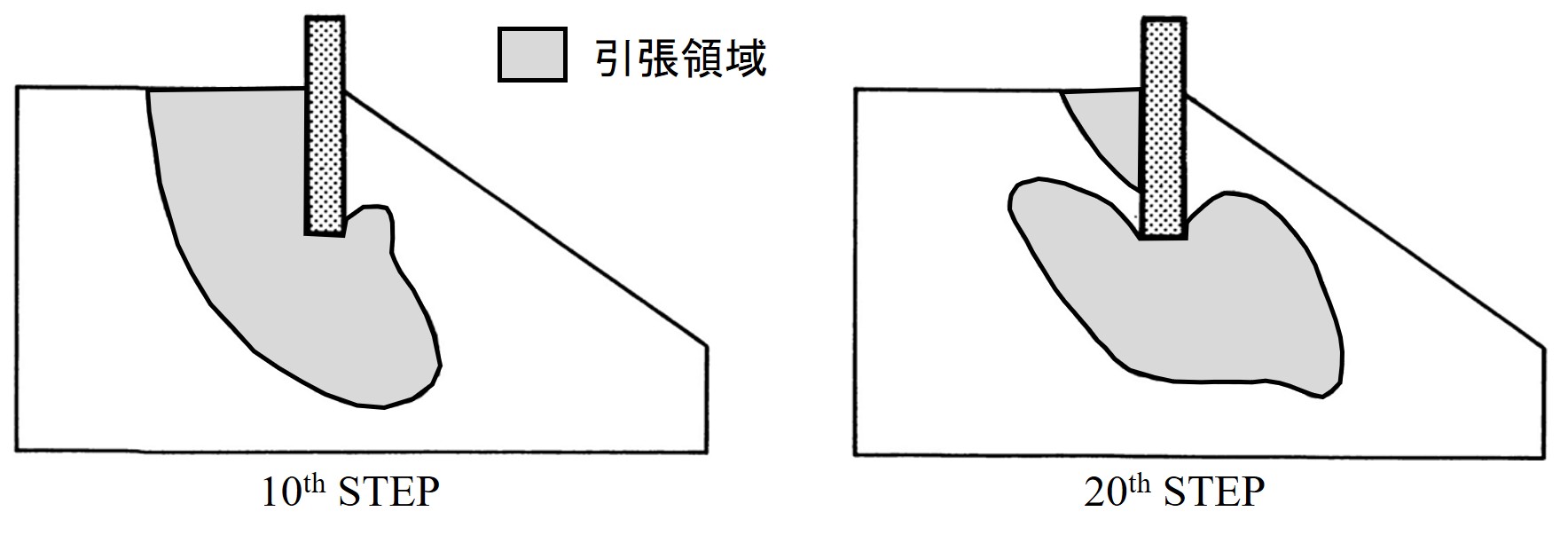
$\hspace{8em}$図2.11　No-TENSION解析結果
 
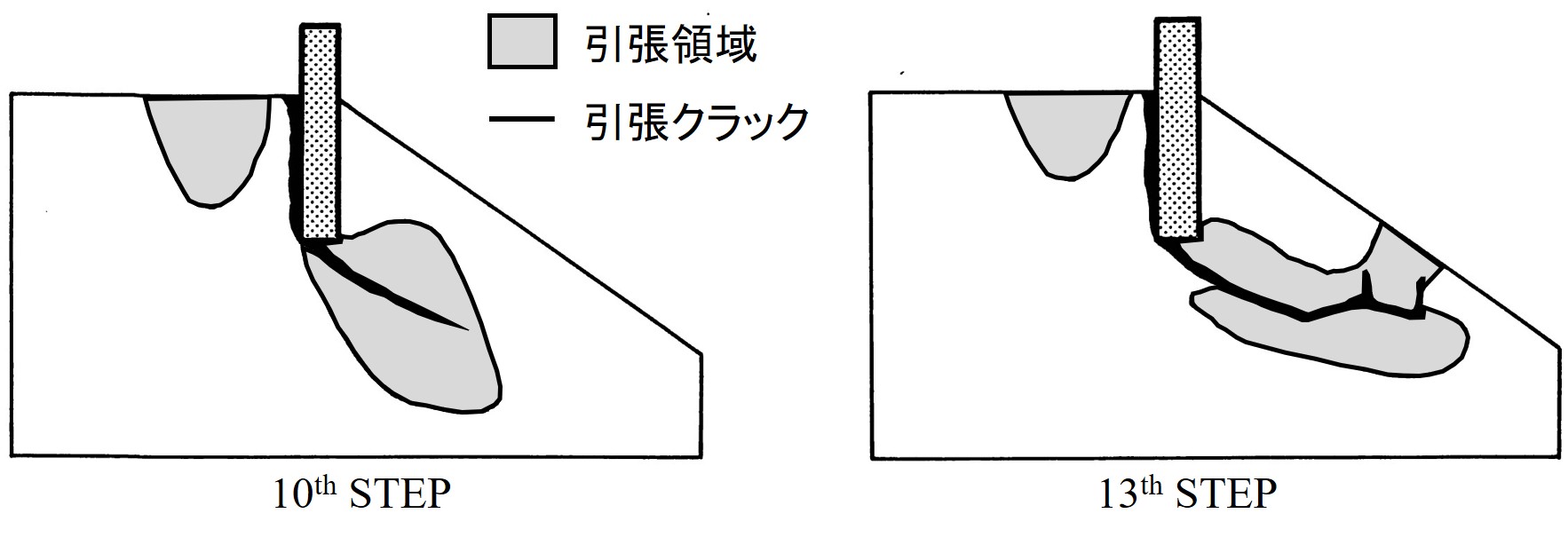
$\hspace{8em}$図2.12　TENSION-CRACK解析結果
 以上のように引っ張りに抵抗しない材料の解析法として、代表的な2つの方法に対する利用法を説明してきたが、ここで取り上げた例題はアルゴリズムをチェックするための簡単な問題であり、地盤力学関連の問題はもちろんのこと、接触問題などへの応用を読者自身で試みるとよいであろう。